WebGL笔记：图形旋转的原理和实现

旋转

1 ）旋转的概念

三维物体的旋转要比位移复杂一点，三维物体的旋转需要满足以下条件：
- 旋转轴
- 旋转方向
- 旋转角度
场景举例
- 模型站在旋转轴的起点进行旋转
- 模型要往左转还是往右转，就是旋转的方向
- 模型旋转的大小就是旋转角度

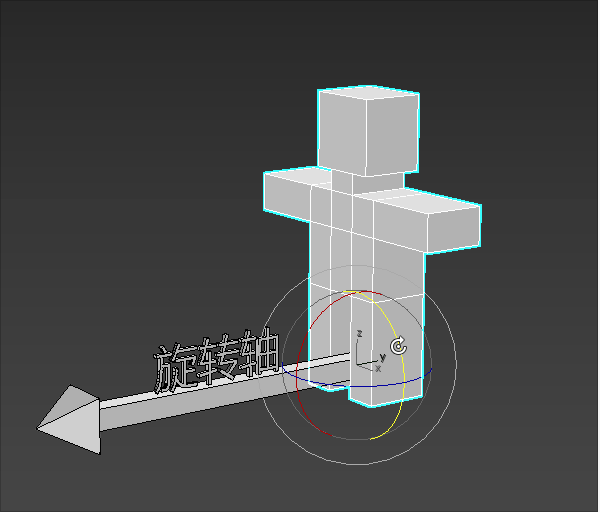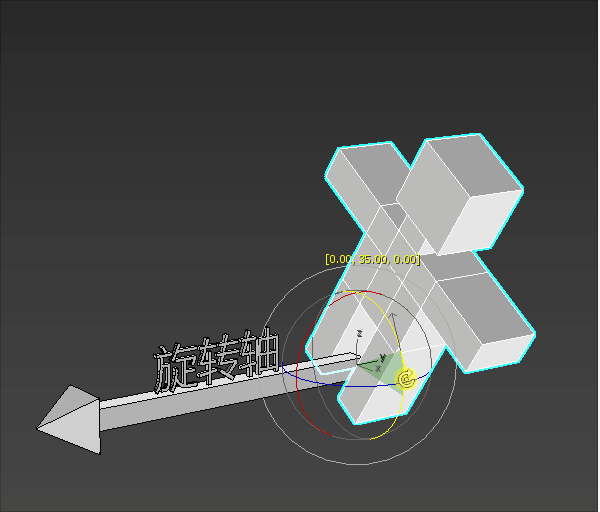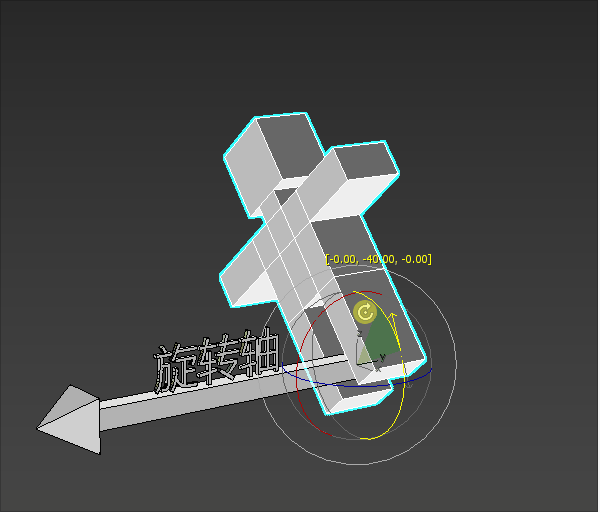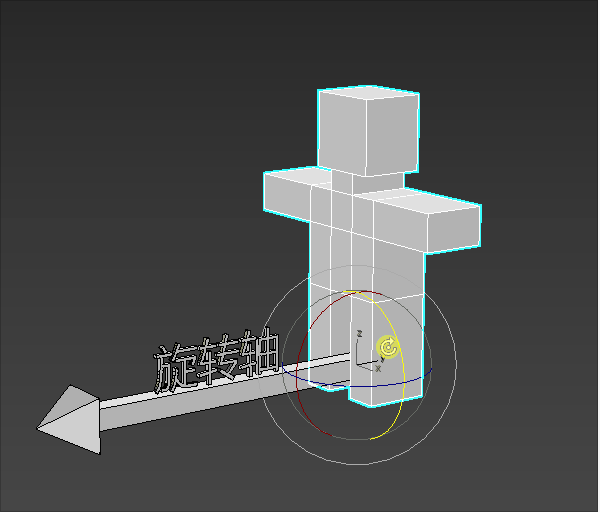
2 ）旋转方向的正负

在webgl中，除裁剪空间之外的大部分功能都使用了右手坐标系
在webgl中，可以暂且将其当成右手坐标系, 下图就是右手坐标系

以上图为例
- 当物体绕 z 轴，从x轴正半轴向y轴正半轴逆时针旋转时，是正向旋转，反之为负。
- 当物体绕 x 轴，从y轴正半轴向z轴正半轴逆时针旋转时，是正向旋转，反之为负。
- 当物体绕 y 轴，从z轴正半轴向x轴正半轴逆时针旋转时，是正向旋转，反之为负。
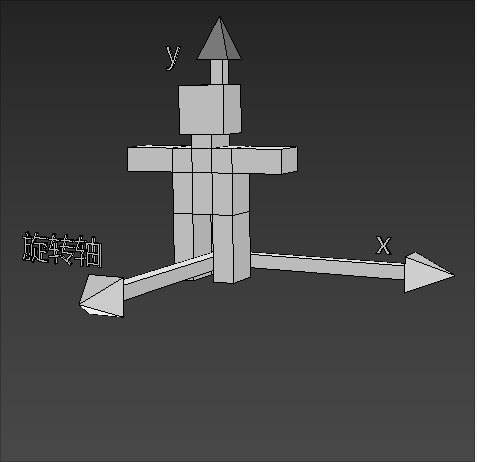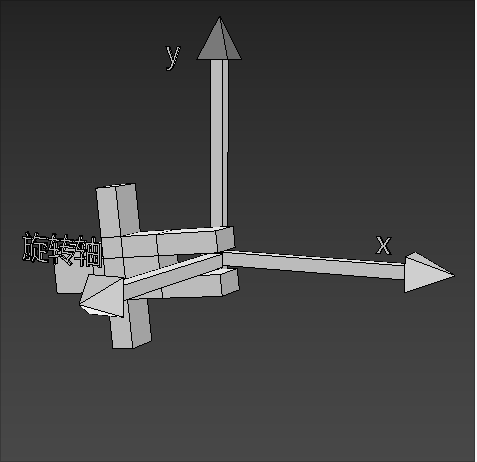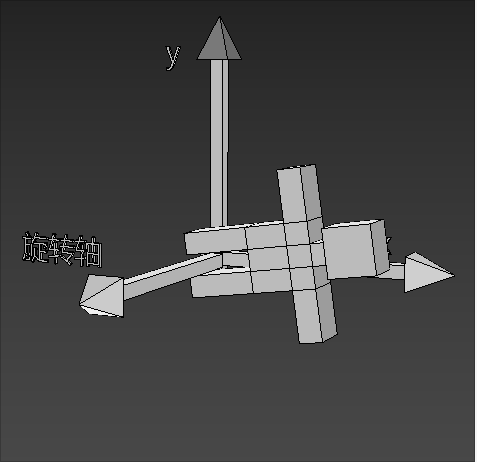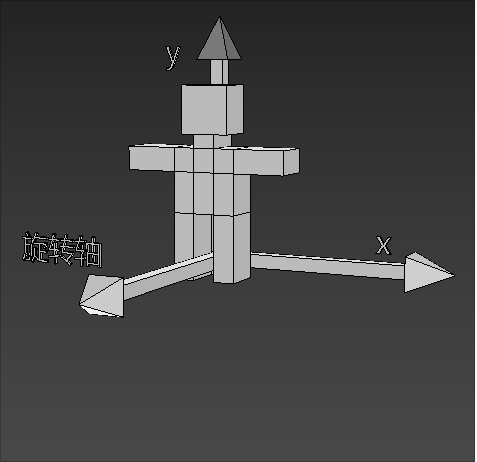
如下图就是正向旋转
- 围绕z轴(骑着z轴)，从x轴到y轴逆时针转动就是正向旋转

旋转公式

如下，让顶点围绕 z 轴旋转的场景

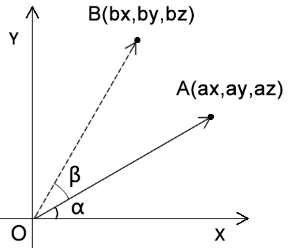
已知
- 点A的位置是(ax,ay,az)
- 点A要围绕z轴旋转β度，转到点B的位置
求：点A旋转后的bx、by位置

解

因为∠β是已知的，∠α 可以通过点 A 得出
所以我们可以得出
```
∠xOB = α + β
```
那我们通过三角函数就可以推出bx、by

设 ∠xOB = θ，则：

bx = cosθ * |OA|
by = sinθ * |OA| // 注意这里因为是旋转, 所以 |OA| === |OB|, 统一用 |OA|来表示

上面的|OA|是点O到点A的距离，可以直接用点A求出
```
|OA| = Math.sqrt(ax * ax + ay * ay)
```
那我们接下来只需要知道cosθ和sinθ的值即可
因为：θ = α + β

所以，我们可以利用和角公式求cosθ和sinθ的值

cosθ = cos(α + β)
cosθ = cosα * cosβ - sinα * sinβ

sinθ = sin(α + β)
sinθ = cosβ * sinα + sinβ * cosα

所以

bx = cosθ * |OA|
bx = (cosα * cosβ - sinα * sinβ) * |OA|
bx = cosα * cosβ * |OA| - sinα * sinβ * |OA|

by = sinθ * |OA|
by = (cosβ * sinα + sinβ * cosα) * |OA|
by = cosβ * sinα * |OA| + sinβ * cosα * |OA|

因为
```
cosα * |OA| = ax
sinα * |OA| = ay
```

所以我们可以简化bx、by的公式

bx = ax * cosβ - ay * sinβ
by = ay * cosβ + ax * sinβ

上面的bx、by就是我们要求的答案

在着色器中旋转

可以直接在着色器里写旋转公式

<script id="vertexShader" type="x-shader/x-vertex">attribute vec4 a_Position;float angle = radians(80.0);float sinB = sin(angle);float cosB = cos(angle);void main() {gl_Position.x = a_Position.x * cosB - a_Position.y * sinB;gl_Position.y = a_Position.y * cosB + a_Position.x * sinB;gl_Position.z = a_Position.z;gl_Position.w = 1.0;}
</script>

radians(float degree) 将角度转弧度
sin(float angle) 正弦
cos(float angle) 余弦

用js旋转图形

我们将顶点着色器里的正弦值和余弦值暴露给js，便可以用js旋转图形了

<script id="vertexShader" type="x-shader/x-vertex">attribute vec4 a_Position;uniform float u_SinB;uniform float u_CosB;void main() {gl_Position.x = a_Position.x * u_CosB-a_Position.y * u_SinB;gl_Position.y = a_Position.y * u_CosB+a_Position.x * u_SinB;gl_Position.z = a_Position.z;gl_Position.w = 1.0;}
</script>

在js 中修改uniform 变量

const u_SinB = gl.getUniformLocation(gl.program, 'u_SinB');
const u_CosB = gl.getUniformLocation(gl.program, 'u_CosB');
const angle = 0.3;
gl.uniform1f(u_SinB, Math.sin(angle));
gl.uniform1f(u_CosB, Math.cos(angle));

之后让图形转起来

!(function ani() {angle += 0.01;gl.uniform1f(u_SinB, Math.sin(angle));gl.uniform1f(u_CosB, Math.cos(angle));gl.clear(gl.COLOR_BUFFER_BIT);gl.drawArrays(gl.TRIANGLES, 0, 3);requestAnimationFrame(ani);
})()

完整代码

<canvas id="canvas"></canvas>
<script id="vertexShader" type="x-shader/x-vertex">attribute vec4 a_Position;uniform float u_SinB;uniform float u_CosB;void main() {gl_Position.x = a_Position.x * u_CosB - a_Position.y * u_SinB;gl_Position.y = a_Position.y * u_CosB + a_Position.x * u_SinB;gl_Position.z = a_Position.z;gl_Position.w = 1.0;}
</script>
<script id="fragmentShader" type="x-shader/x-fragment">void main() {gl_FragColor = vec4(1.0,1.0,0.0,1.0);}
</script>
<script type="module">import { initShaders } from './utils.js';const canvas = document.getElementById('canvas');canvas.width = window.innerWidth;canvas.height = window.innerHeight;const gl = canvas.getContext('webgl');const vsSource = document.getElementById('vertexShader').innerText;const fsSource = document.getElementById('fragmentShader').innerText;initShaders(gl, vsSource, fsSource);const vertices = new Float32Array([0.0, 0.1,-0.1, -0.1,0.1, -0.1]);const vertexBuffer = gl.createBuffer();gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer);gl.bufferData(gl.ARRAY_BUFFER, vertices, gl.STATIC_DRAW);const a_Position = gl.getAttribLocation(gl.program, 'a_Position');gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, 0, 0);gl.enableVertexAttribArray(a_Position);// 获取Uniform变量const u_SinB = gl.getUniformLocation(gl.program, 'u_SinB')const u_CosB = gl.getUniformLocation(gl.program, 'u_CosB')// 修改uniform 变量let angle = 0.3gl.uniform1f(u_SinB, Math.sin(angle))gl.uniform1f(u_CosB, Math.cos(angle))gl.clearColor(0.0, 0.0, 0.0, 1.0);gl.clear(gl.COLOR_BUFFER_BIT);gl.drawArrays(gl.TRIANGLES, 0, 3);!(function ani() {angle += 0.01;gl.uniform1f(u_SinB, Math.sin(angle));gl.uniform1f(u_CosB, Math.cos(angle));gl.clear(gl.COLOR_BUFFER_BIT);gl.drawArrays(gl.TRIANGLES, 0, 3);requestAnimationFrame(ani);})()
</script>