一、实验目的

1.掌握用 matlab 分析系统时间响应的方法

2.掌握用 matlab 分析系统频率响应的方法

3.掌握系统零、极点分布与系统稳定性关系

二、实验原理

1. 系统函数 H(s)

系统函数:系统零状态响应的拉氏变换与激励的拉氏变换之比.

 H(s)=R(s)/E(s)

在 matlab 中可采用多种方法描述系统,本文采用传递函数(系统函数)描述法. 在 matlab

中, 传递函数描述法是通过传递函数分子和分母关于 s 降幂排列的多项式系数来表示的.例

如,某系统传递函数如下

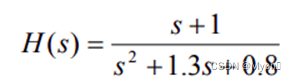
则可用如下二个向量 num 和 den 来表示:

num=[1,1]

den=[1,1.3,0.8]

2. 用 matlab 分析系统时间响应

1)脉冲响应

 y=impulse(num,den,T)

T:为等间隔的时间向量,指明要计算响应的时间点.

2)阶跃响应

y=setp(num,den,T)

T 同上.

3)对任意输入的响应

y=lsim(num,den,U,T)

U:任意输入信号. T 同上.

例:对式(1)系统,分别求脉冲响应、阶跃响应及对输入 u(t)=sin(t)的响应.

num=[1,1];

den=[1,1.3,0.8];

T=0:0.1:3;

y1=impulse(num,den,T);

y2=step(num,den,T);

U=sin(T);

y3=lsim(num,den,U,T);

subplot(2,2,1);plot(T,y1);title('脉冲响应')

subplot(2,2,2);plot(T,y2);title('阶跃响应')

subplot(2,2,3);plot(T,y3);title('输入为 u=sint 的响应')