西工大网络空间安全学院计算机系统基础实验一（45678）

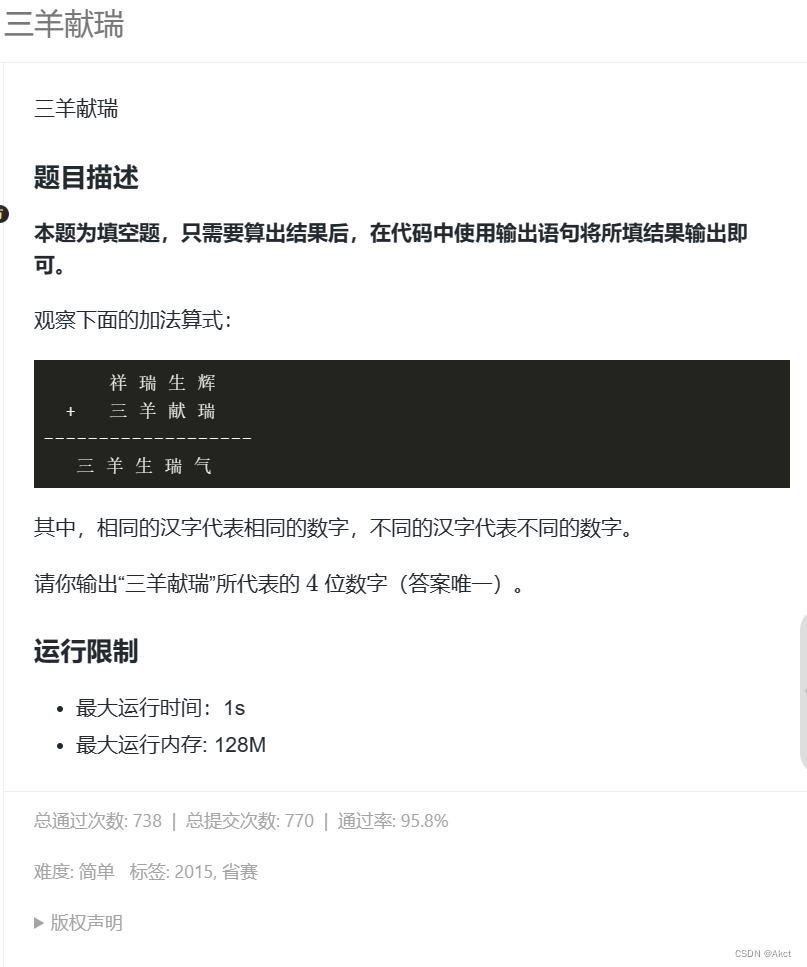
接着来看第4个函数，int replaceByte(int x, int n, int c)，看题目给出的例子，replaceByte(0x12345678,1,0xab) = 0x1234ab78。我们可以多写几个例子，进而找出规律，比如：

replaceByte(0x12345678,2,0xab) = 0x12ab5678

replaceByte(0x12345678,3,0xab) = 0xab345678

replaceByte(0x12345678,0,0xab) = 0x123456ab

replaceByte(0x12345678,1,0x00) = 0x12340078

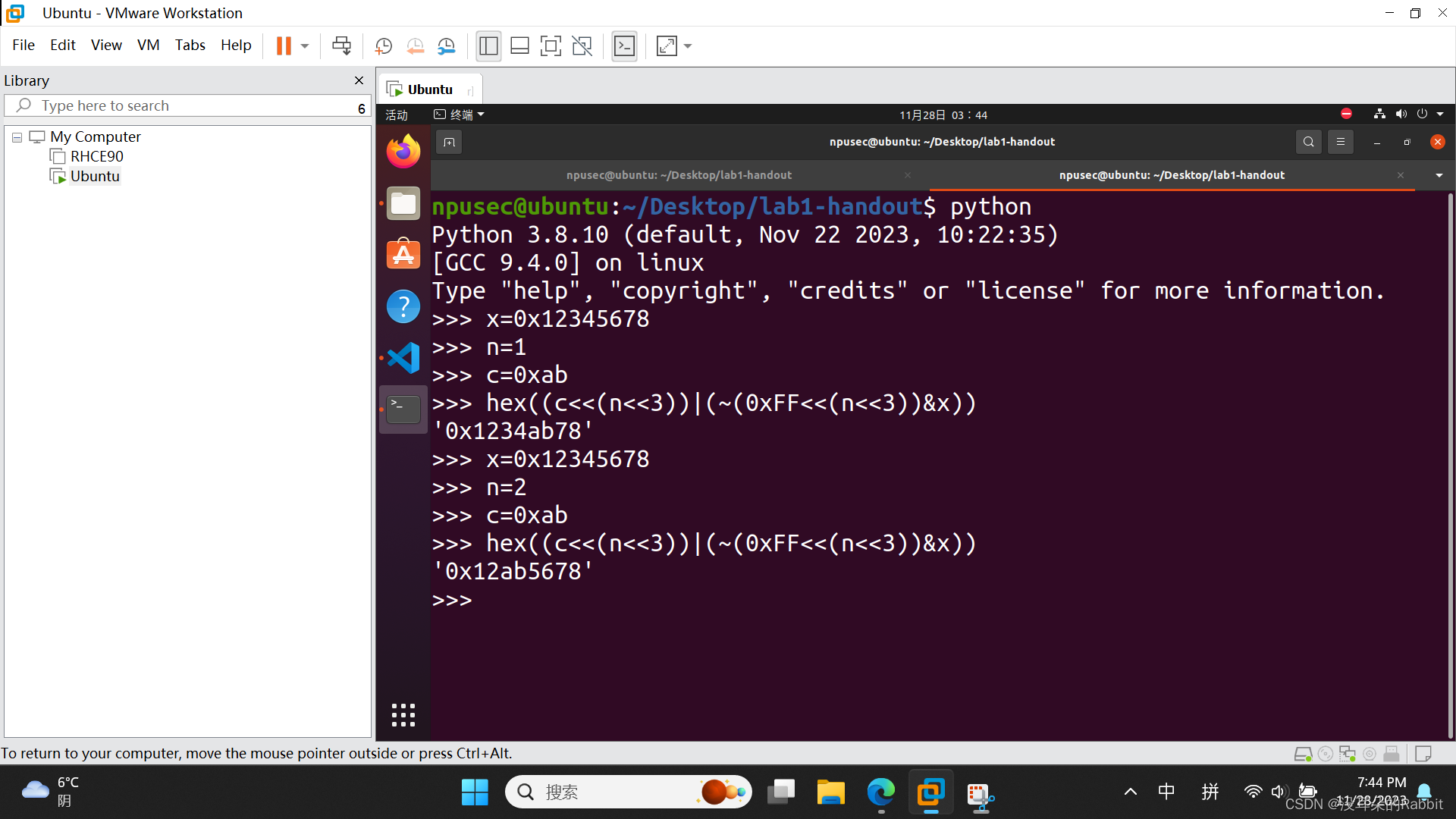
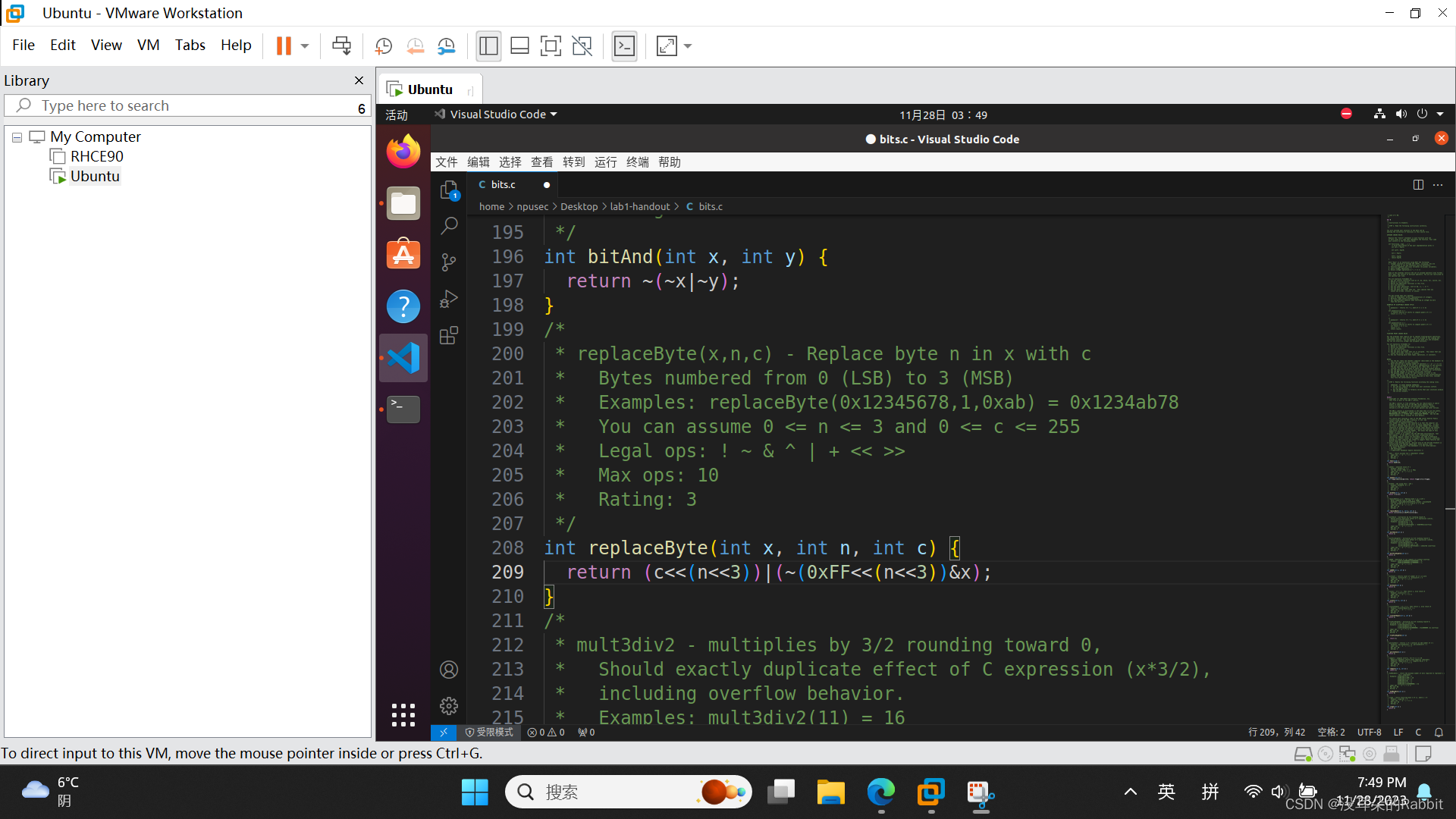
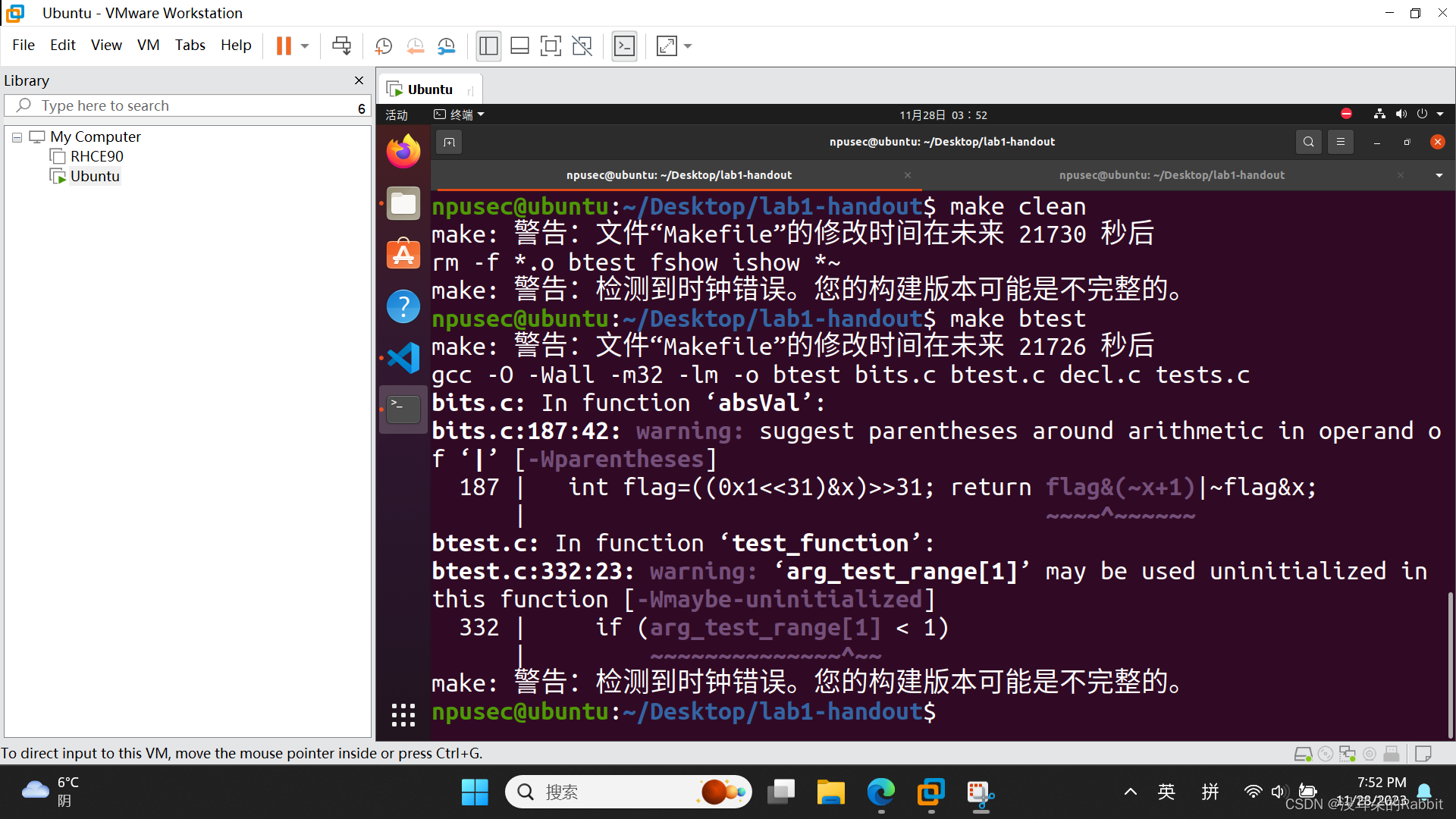
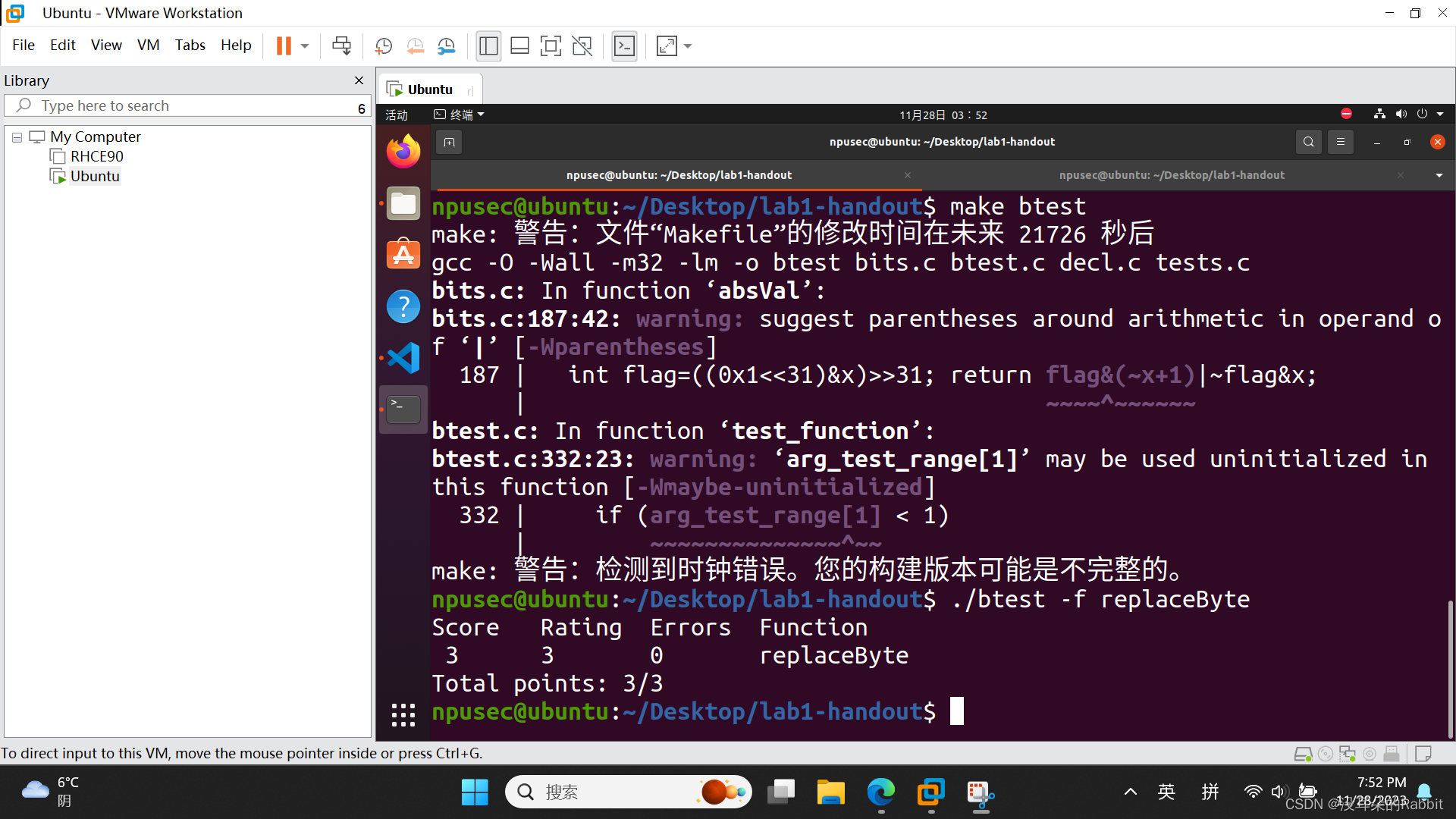
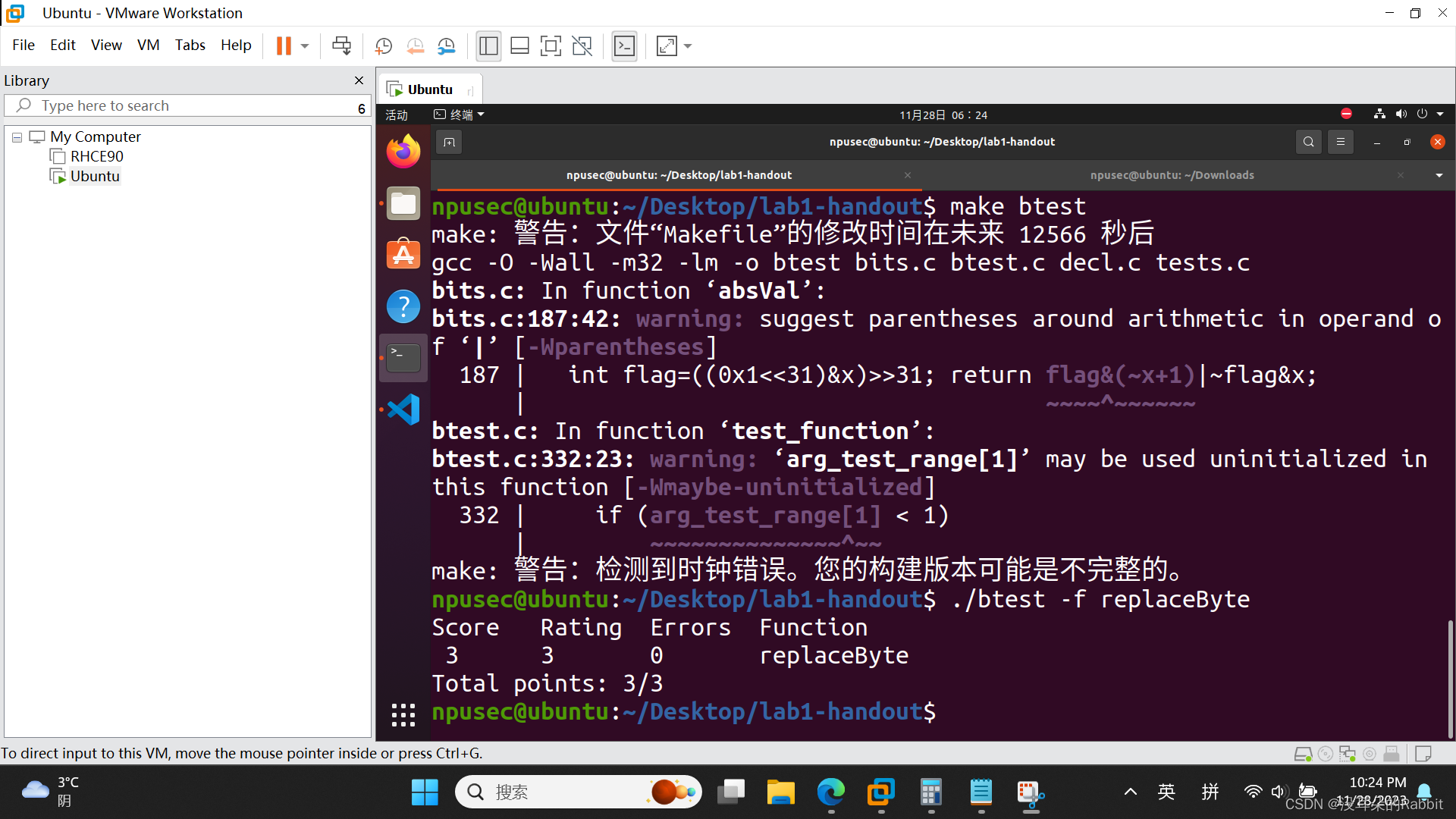
由此我们猜测，返回值可能是(c<<(n<<3))|(~(0xFF<<(n<<3))&x)，为什么呢？我们拿题目给的例子为例来讲。replaceByte(0x12345678,1,0xab) = 0x1234ab78，结果可以看成由0x0000ab00与0x12340078相或得到，那么该怎么得到0x0000ab00与0x12340078呢？发现0xab<<8即可得到0xab00，而0xab<<8 == 0xab<<(1<<3)，进而发现可以通过(c<<(n<<3))得到0x0000ab00，接着如何得到0x12340078呢？发现0x12340078可由0x12345678&0xFFFF00FF得到，而x即为0x12345678，那么该如何得到0xFFFF00FF呢？发现0xFFFF00FF==~0x0000FF00，而0x0000FF00==0xFF<<(1<<3)，即0xFF<<(n<<3)。所以综上所述，我们得到了(c<<(n<<3))|(~(0xFF<<(n<<3))&x)，下面我们使用Python进行检验，如（图1：第4个函数——用Python验证想法）所示。经过Python验证，我们的想法是正确的，接着我们重复第1、2、3个函数的流程，使用VS code修改bits.c文件，使用"./dlc bits.c"与"./dlc -e bits.c"命令确保第4个函数中使用的运算符等满足要求，使用"make clean", "make btest"函数编译生成新的btest可执行文件，使用"./btest -f replaceByte"命令保证函数能产生正确的结果。如（图2：第4个函数）所示，成功编写第4个函数。

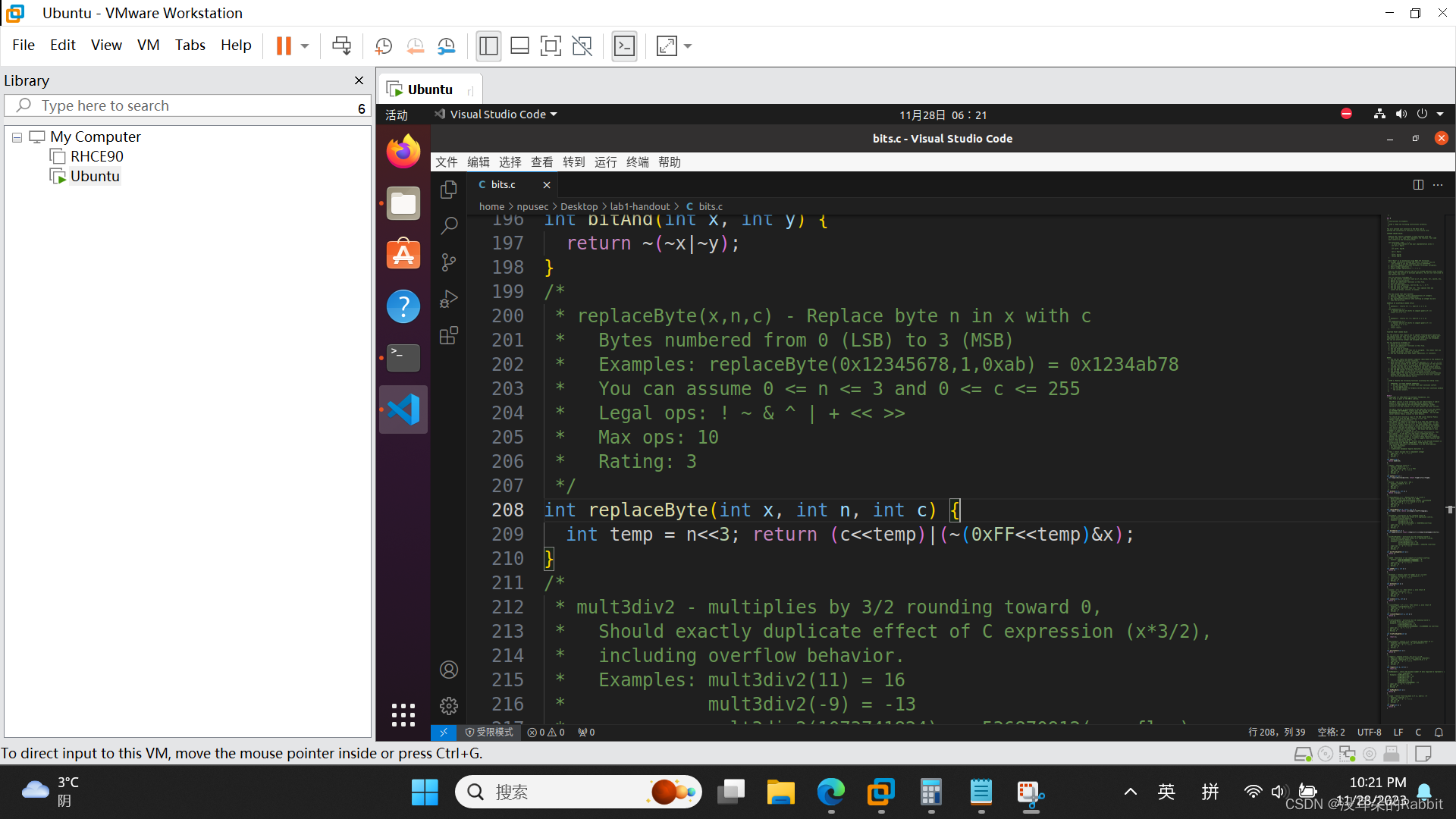
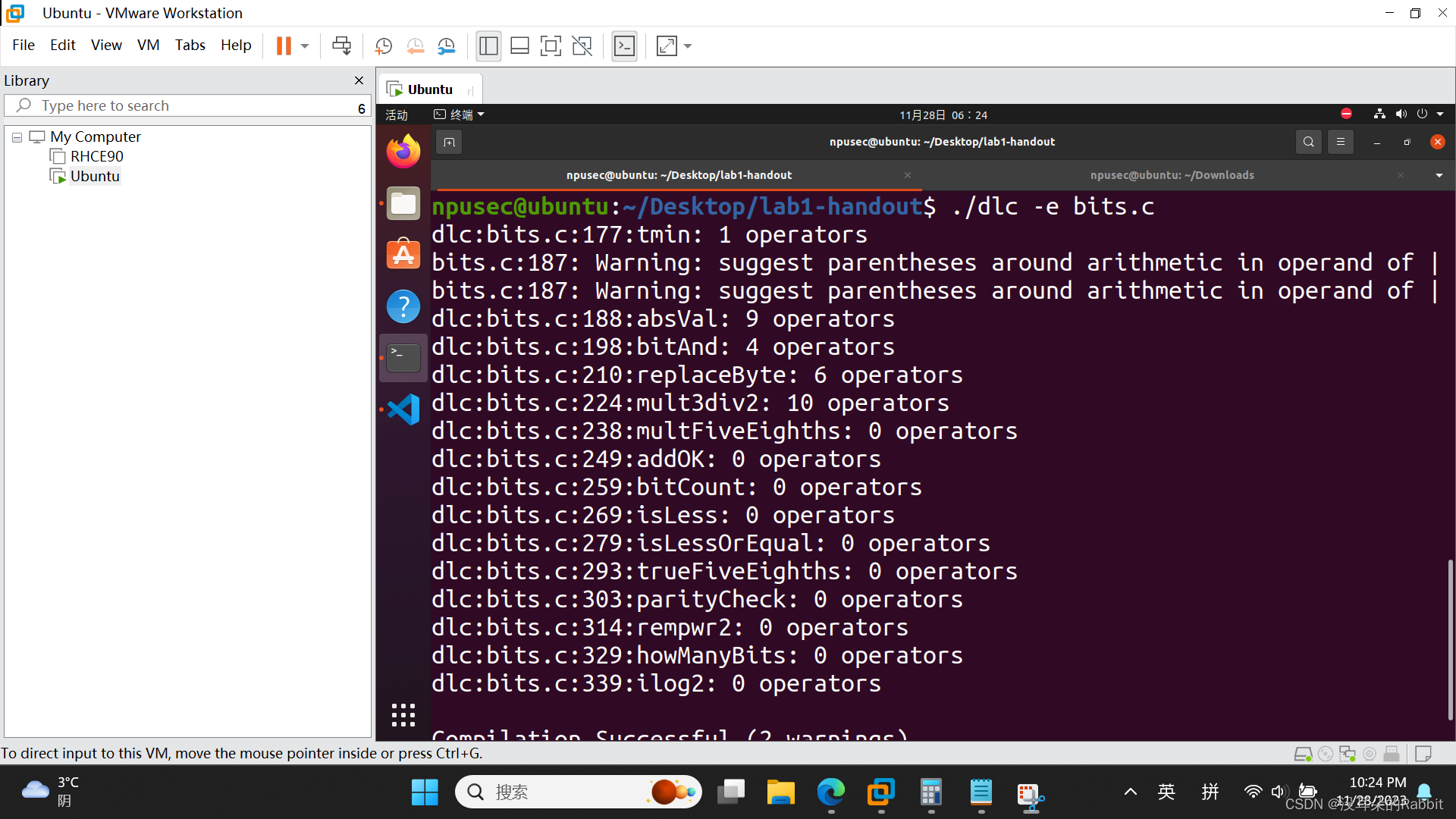
另外，发现第4个函数还可以再次修改，使得使用到的运算符再少一个，如（图3：优化后的第4个函数）所示。

**************************************************************************************************************

（图1：第4个函数——用Python验证想法）

**************************************************************************************************************

（图2：第4个函数）

**************************************************************************************************************

（图3：优化后的第4个函数）

**************************************************************************************************************

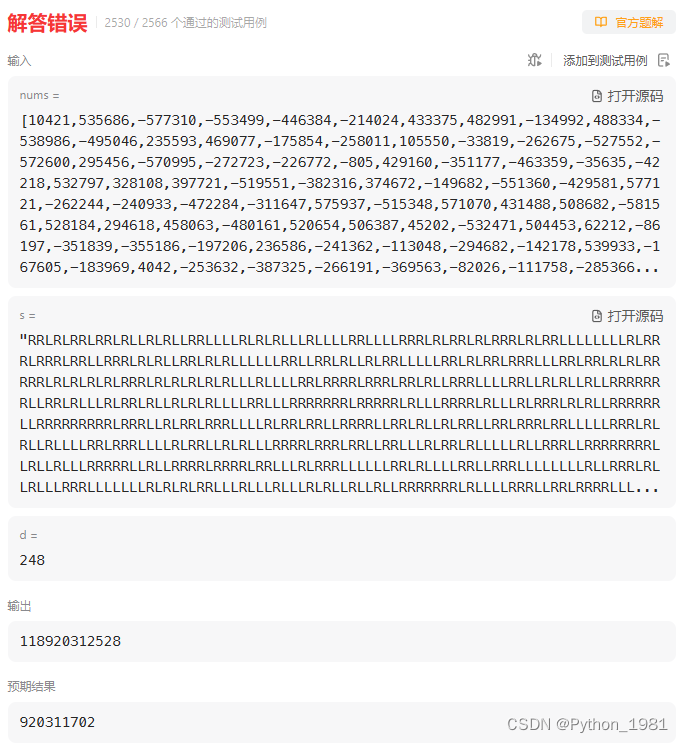
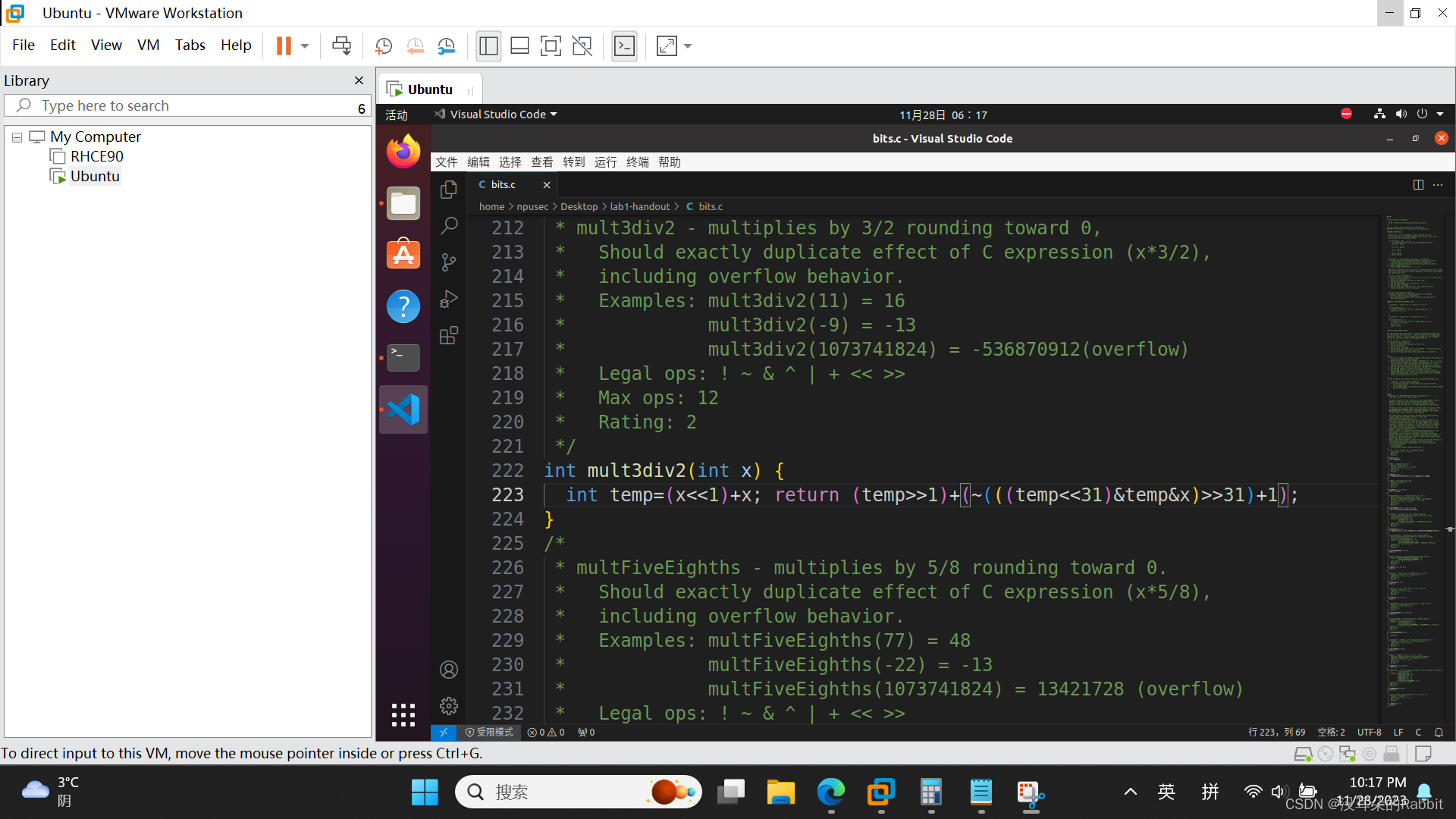
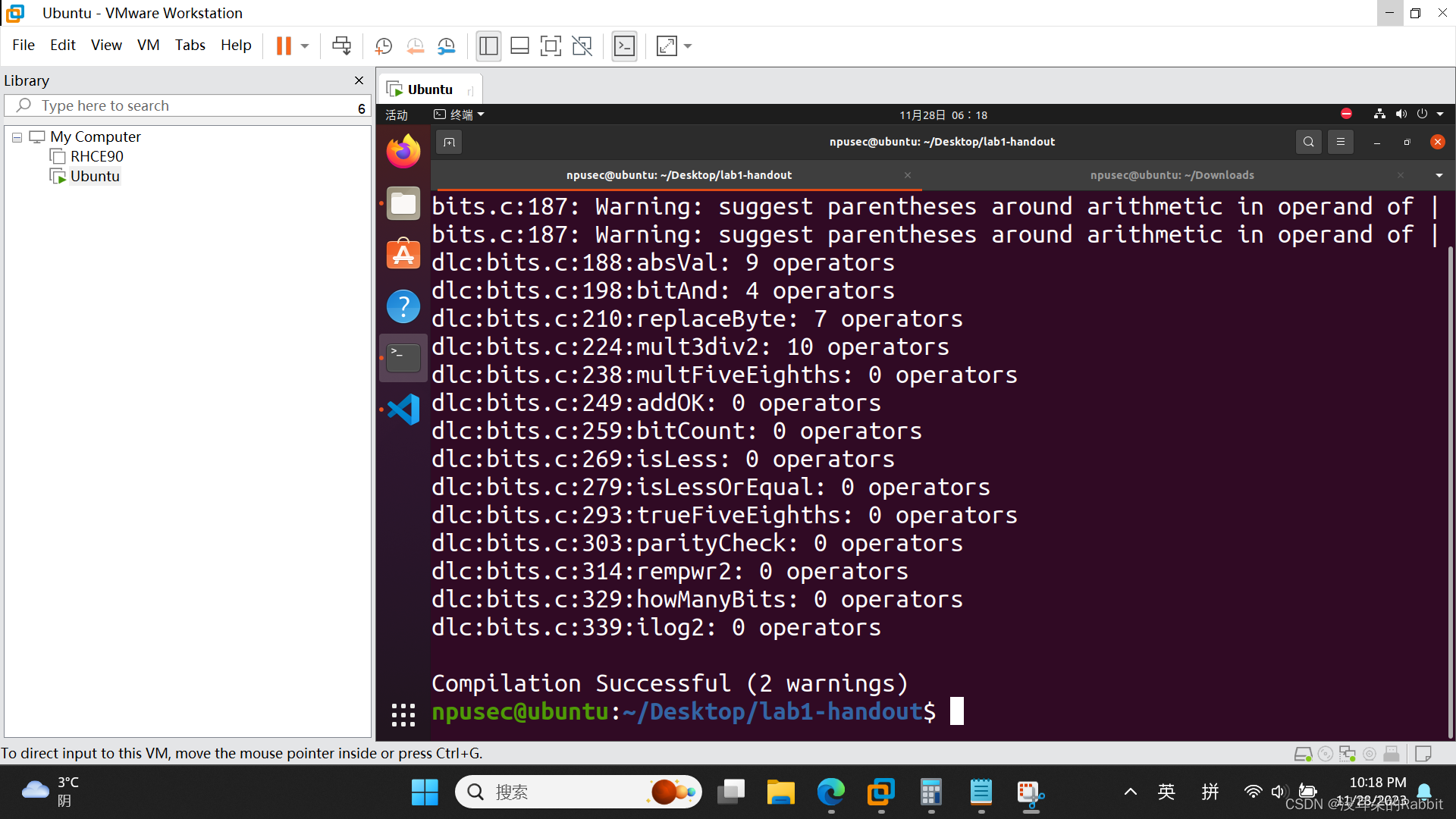
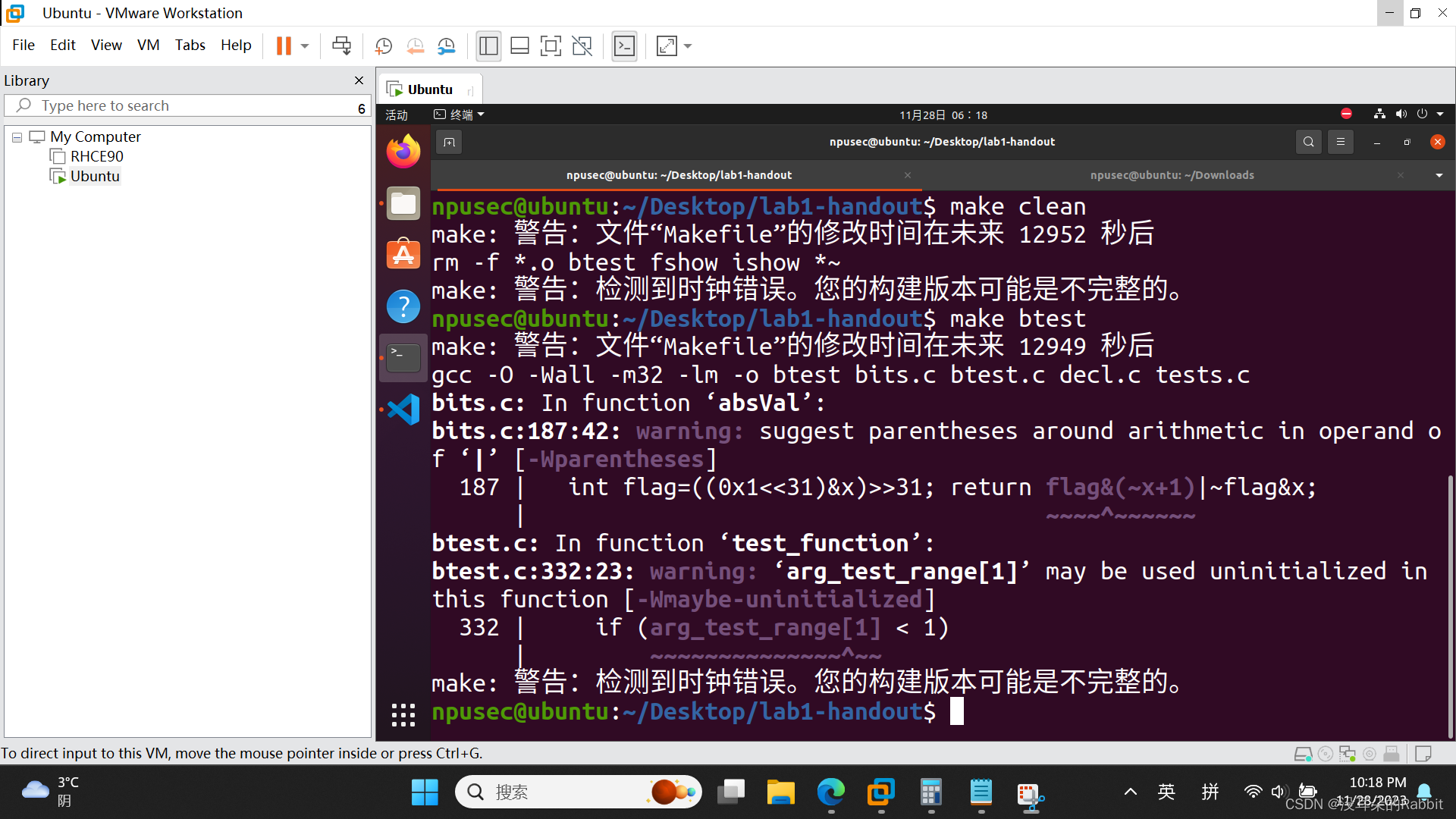
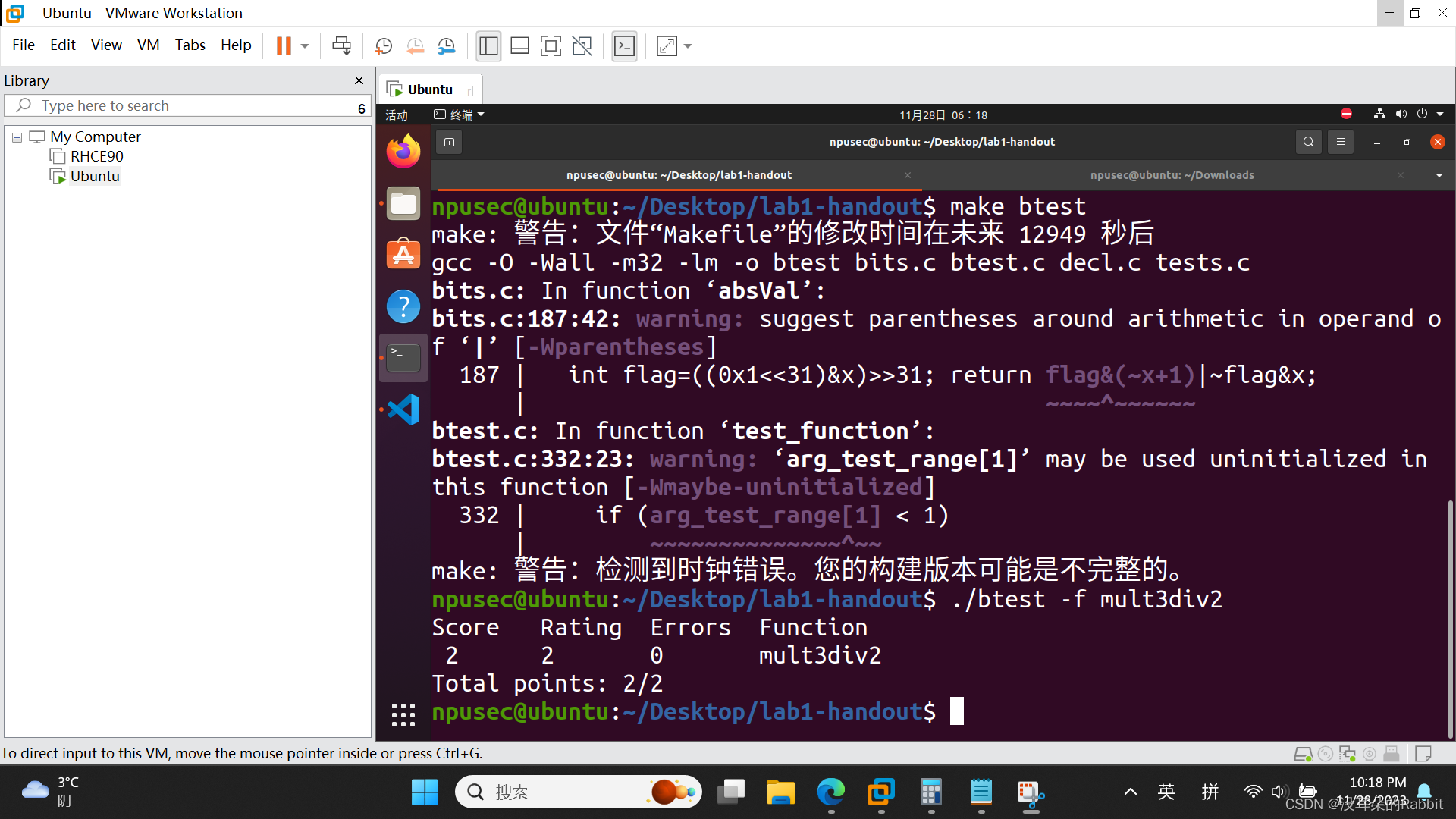
接着看第5个函数，int mult3div2(int x)，看题目给出的三个例子：mult3div2(11) = 16; mult3div2(-9) = -13; mult3div2(1073741824) = -536870912(overflow)。先看第一个例子，mult3div2(11) = 16，11的十六进制形式为0xB, (0xB<<1)+0xB可以得到0x21，接着0x21>>1得到0x1，十进制形式为16，正好是第一个例子的结果。虽然如此，我们依然可以留心到0x21右移一位时，最低位的1被移走了，但是歪打正着，正好满足了向0舍入的要求。所以我们猜测，返回的表达式是((x<<1)+x)>>1。第二个例子，mult3div2(-9) = -13，-9的16进制形式为0xFFFF FFF7，((0xFFFF FFF7)<<1)+(0xFFFF FFF7)可以得到0xFFFF FFE5，接着0xFFFF FFE5>>1得到0xFFFF FFF2，十进制形式为-14。但是期望中的结果是-13，而不是-14。这时我们发现，0xFFFF FFE5右移一位时，最低位的1被移走了，而且与向0舍入背道而驰。第三个例子，mult3div2(1073741824) = -536870912(overflow)，1073741824的十六进制形式为0x4000 0000，(0x4000 0000<<1)+0x4000 0000可以得到0xC000 0000，0xC000 0000>>1得到0xE000 000，十进制形式即为-536,870,912，正好是答案的形式。

现在整理一下，只有当(x<<1)+x的最低位为1，并且x的最高位也为1时，返回的结果需要在((x<<1)+x)>>1的基础上，再多加1，否则不需要加1，直接返回((x<<1)+x)>>1即可。但是，真的是这样子嘛？？？作者私底下偷偷试过几次，发现还需要添加一条附加条件：(x<<1)+x的最高位也为1。那么如何用表达式表示出来“(x<<1)+x的最低位为1、最高位为1，并且x的最高位也为1”呢？((((x<<1)+x)<<31)&((x<<1)+x)&x)>>31。因为(x<<1)+x被反复使用，所以为了节省运算符，我们选择设置temp=(x<<1)+x，这样子即可写作：((temp<<31)&temp&x)>>31。只有当(x<<1)+x的最低位为1，最高位为1，并且x的最高位也为1时，((temp<<31)&temp&x)>>31的结果为0xFFFFFFFF，否则即为0。注意！！！在这里千万不要简单的将((x<<1)+x)>>1与((temp<<31)&temp&x)>>31相加！！！应该将((temp<<31)&temp&x)>>31取反后加1，即~(((temp<<31)&temp&x)>>31)+1，然后再与((x<<1)+x)>>1相加，才是正确的表达式子。作者就是因为这个错误，改了好一会。仿照着第1、2、3、4个函数的方法，我们来检验我们的函数对不对。如（图4：第5个函数）所示。

最后，至于为什么要添加那一条，作者并不清楚，等以后有时间慢慢研究吧。

**************************************************************************************************************

（图4：第5个函数）

**************************************************************************************************************

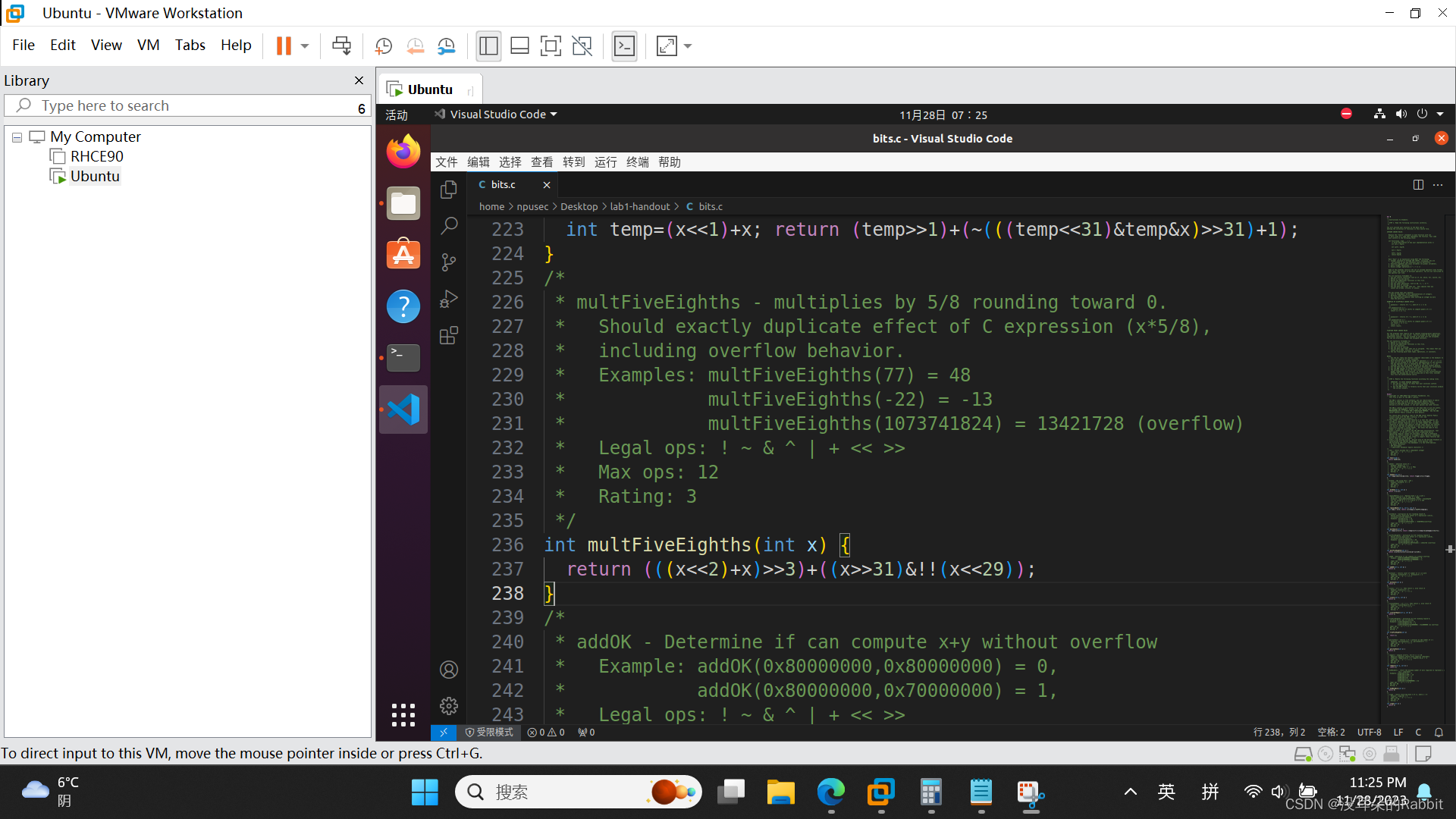
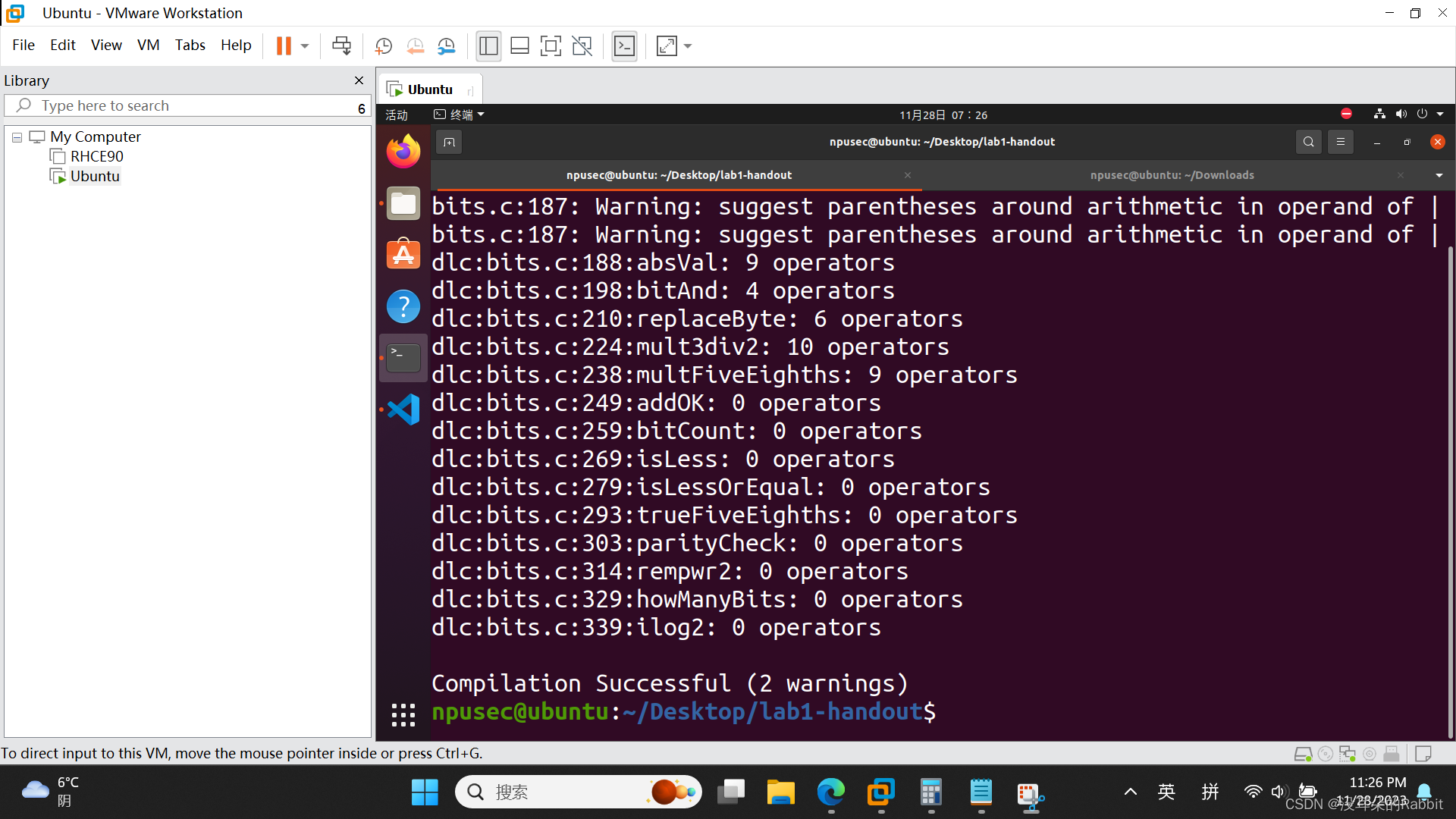
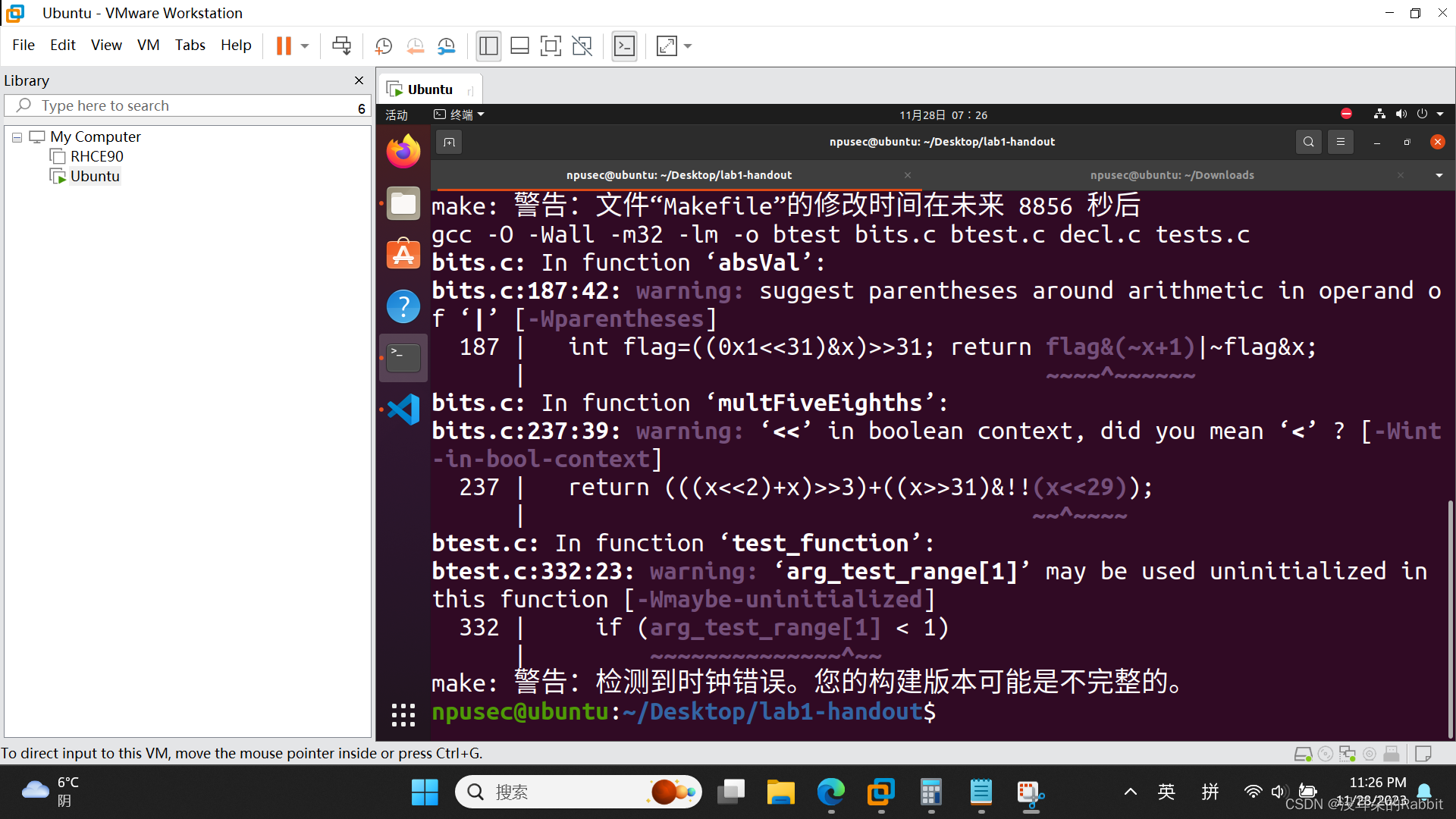
第6个函数，int multFiveEighths(int x) ，执行效果应该类似于C语言中的x*5/8，而且向0舍入。这道题比第5题的难度更大。但我们不妨采用类似的方法，先确定大概的轮廓((x<<2)+x)>>3，接着再去细调。而细调的方法是，不断比较对于不同的x，两个表达式((x<<2)+x)>>3与x*5/8的值是否会有不同，以及会有多大的不同。观察发现似乎对于0到2147483647的正整数来说，((x<<2)+x)>>3与x*5/8的值相同，对于-1到-2147483648的负数来说，除非该负数能够整除8，否则 x*5/8=(((x<<2)+x)>>3)+1。而如果x这个负数能够整除8，则x<<29为0x0，并且x>>31=0xFFFF FFFF，写在一起即为(x>>31)&!(x<<29)。所以最终返回的表达式是：(((x<<2)+x)>>3)+((x>>31)&!!(x<<29))（注意这里采用了两个取非符号！！！这个地方很容易错）。仿照第1、2、3、4、5个函数的方法，我们来检验第6个函数的正确性，如（图5：第6个函数）所示。

**************************************************************************************************************

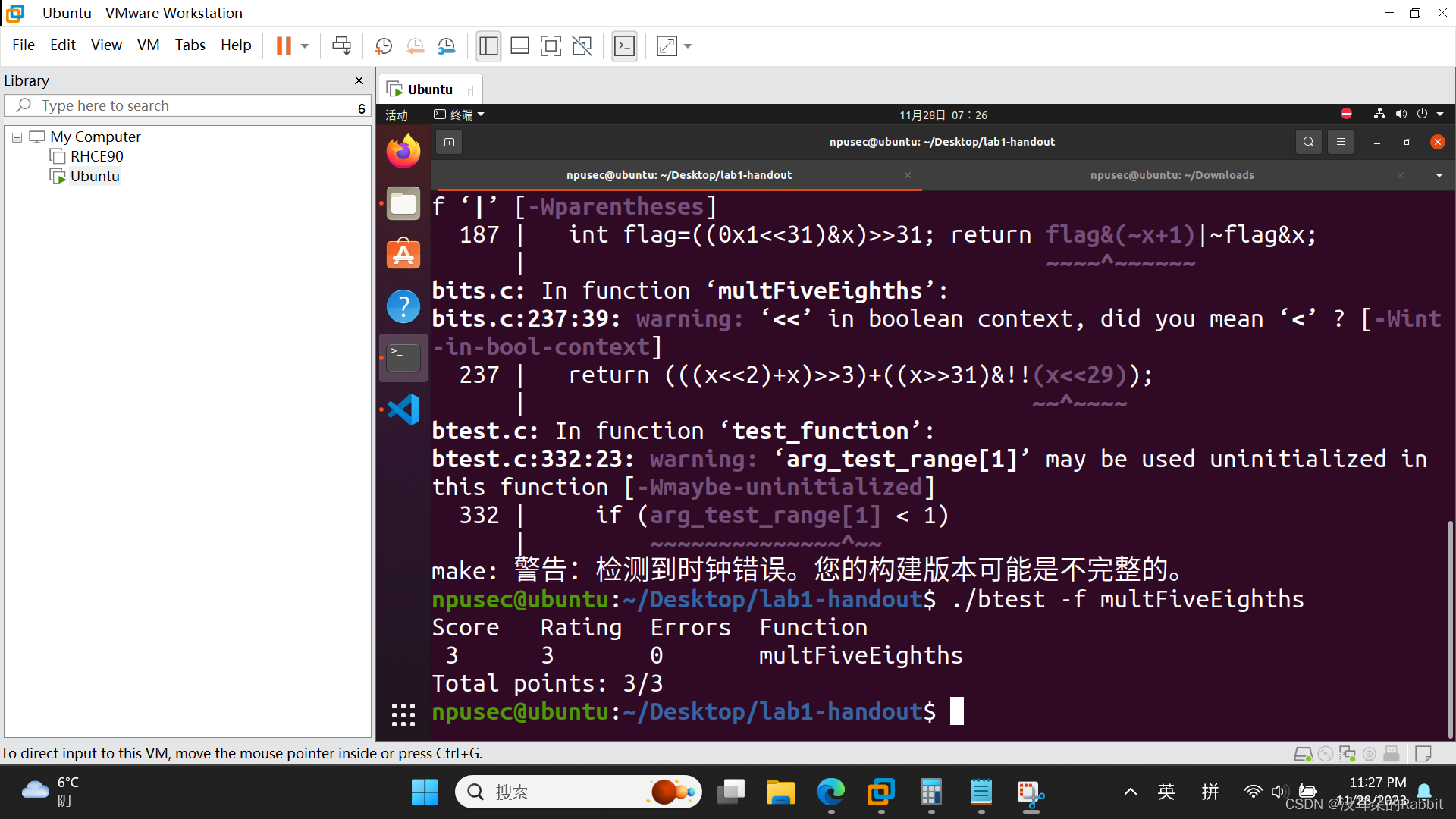
（图5：第6个函数）

**************************************************************************************************************

第7个函数，int addOK(int x, int y)，判断x+y是否会发生溢出。如果会发生溢出，那么返回0，如果不会发生溢出，则返回1。而两个int类型变量相加会造成溢出的情况是：当两个正数相加得到的结果为负数，或者两个负数相加得到的结果为正数时，就会发生溢出。用"int sum=x+y"来保存x+y的值。返回!((~((x>>31)^(y>>31)))&((x>>31)^(sum>>31)))。虽然最终通过了，如（图6：第7个函数）所示，但是其中的函数逻辑并没有理清楚，还需要进行一轮又一轮的迭代与优化。

**************************************************************************************************************

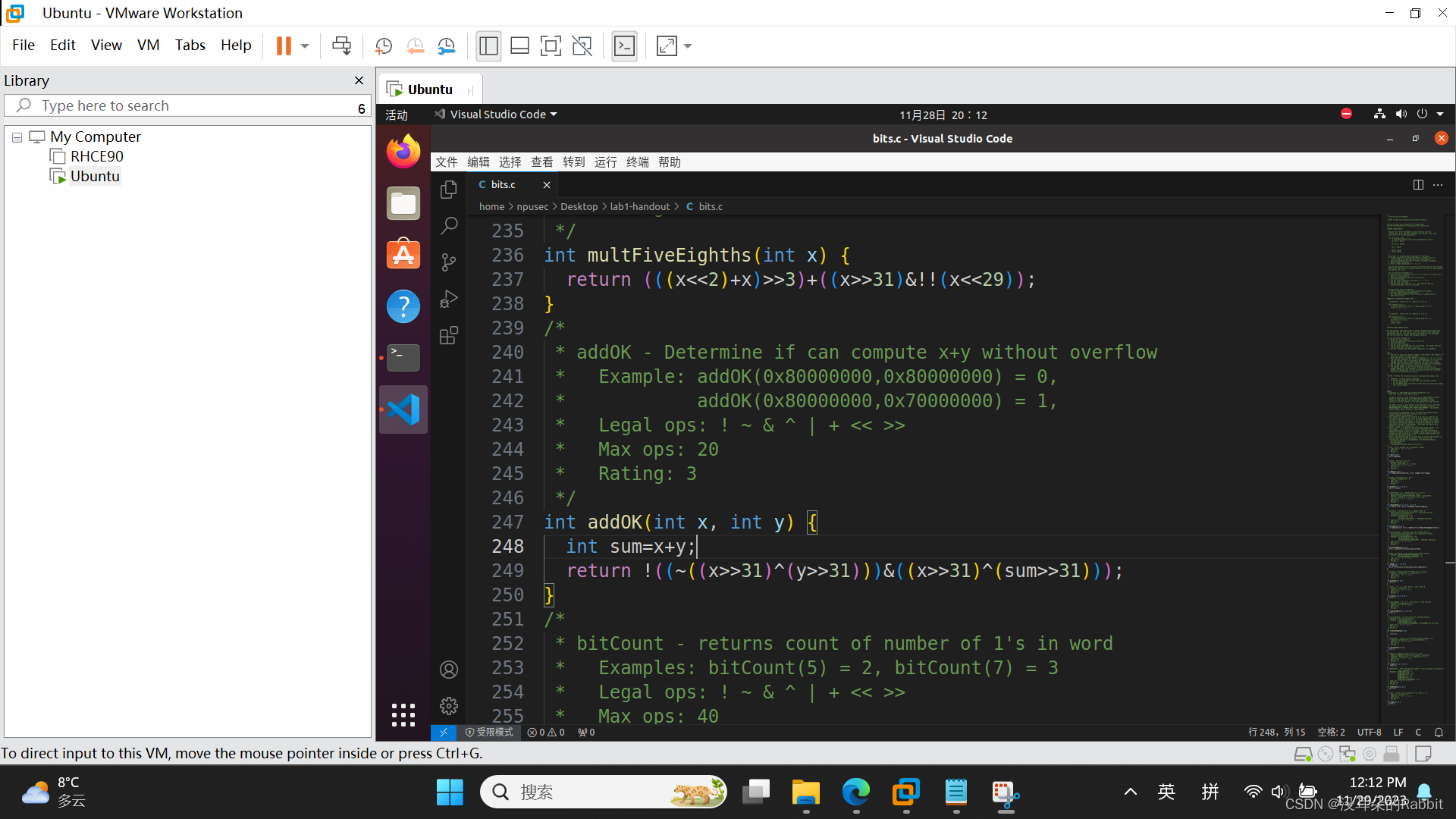
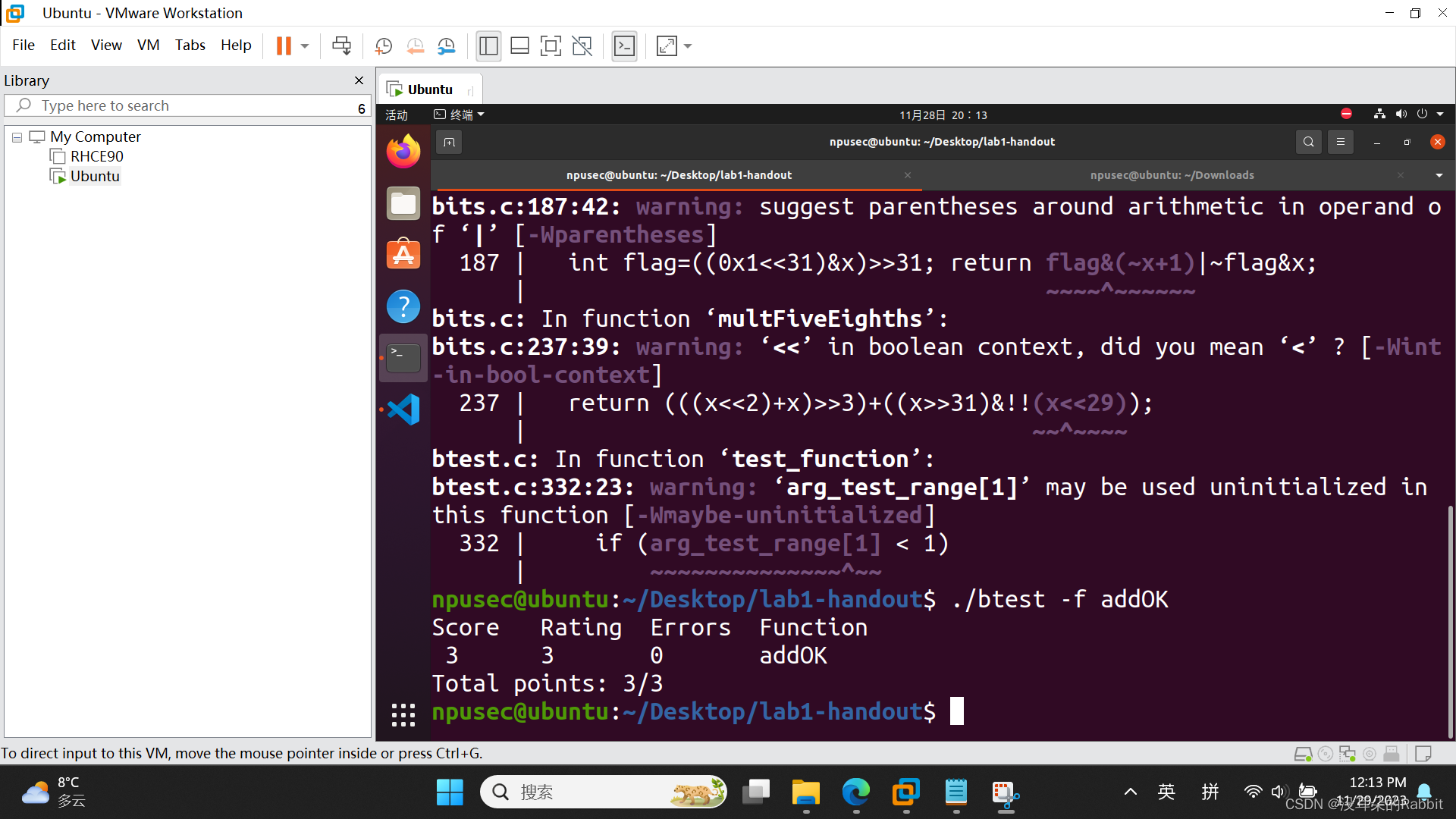
（图6：第7个函数）

**************************************************************************************************************

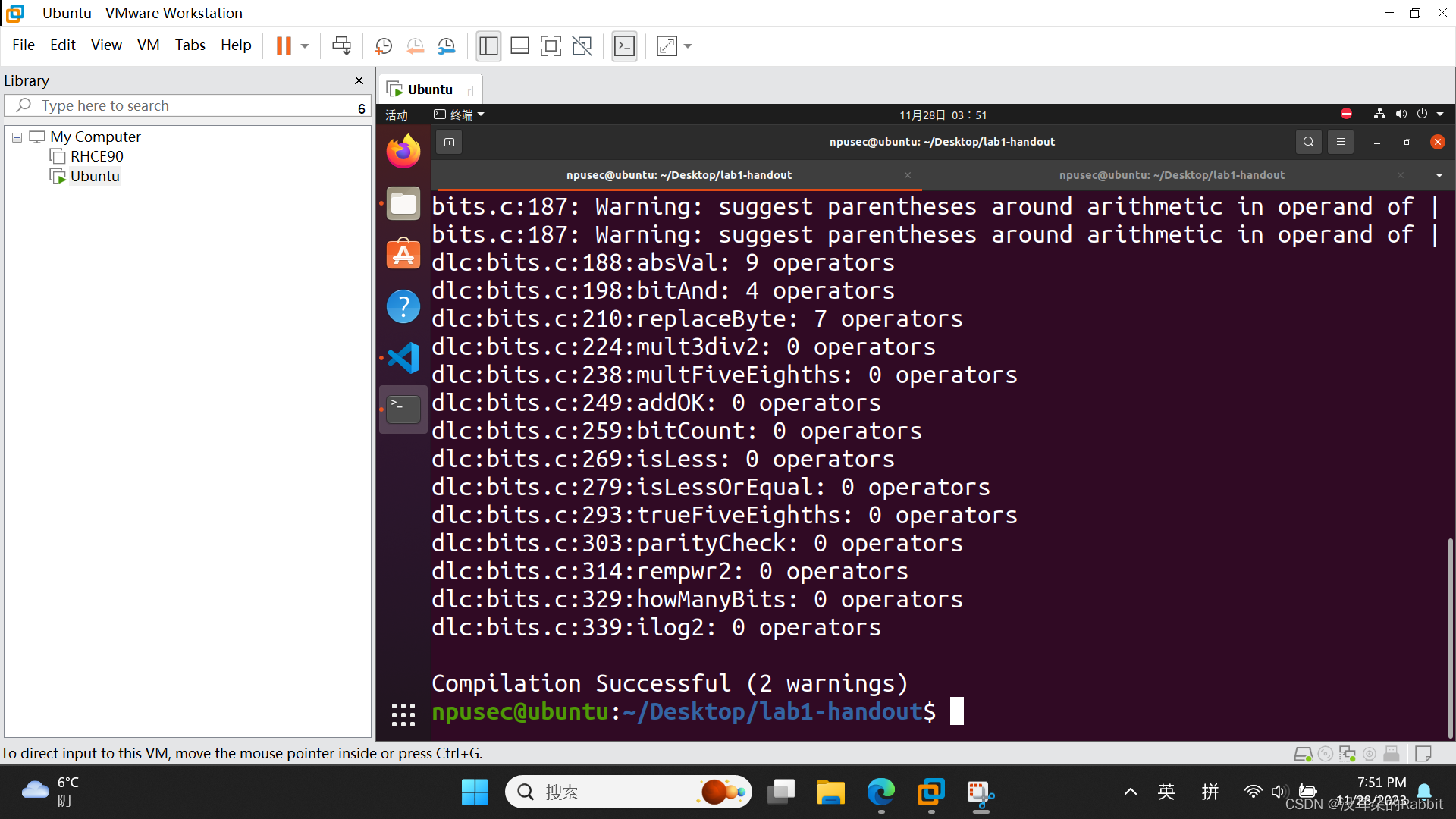
第8个函数，int bitCount(int x)，返回int型变量x的十六进制表示形式中1的个数。比如当x=5时，5为0x0101，有2个1，当x=7时，7为0x0111，有3个1。这道题比较复杂，使用到了“汉明重量”的知识。作者结合Java中对于函数bitCount的实现方法，简单修改了下代码，使其满足对于运算符等的要求，之后按照前7个函数相同的方法，写完了第8个函数，如（图7：第8个函数）所示：

**************************************************************************************************************

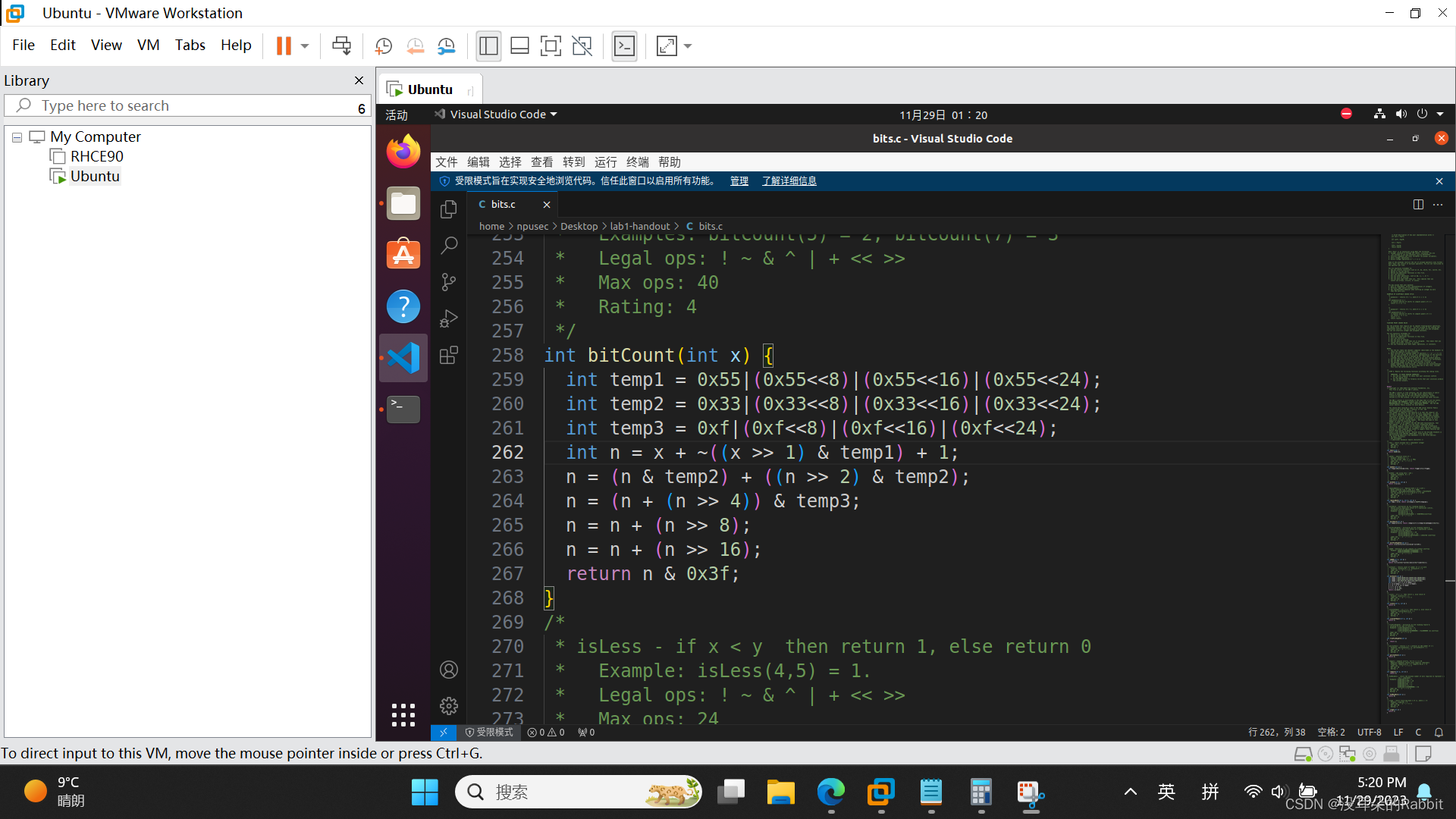
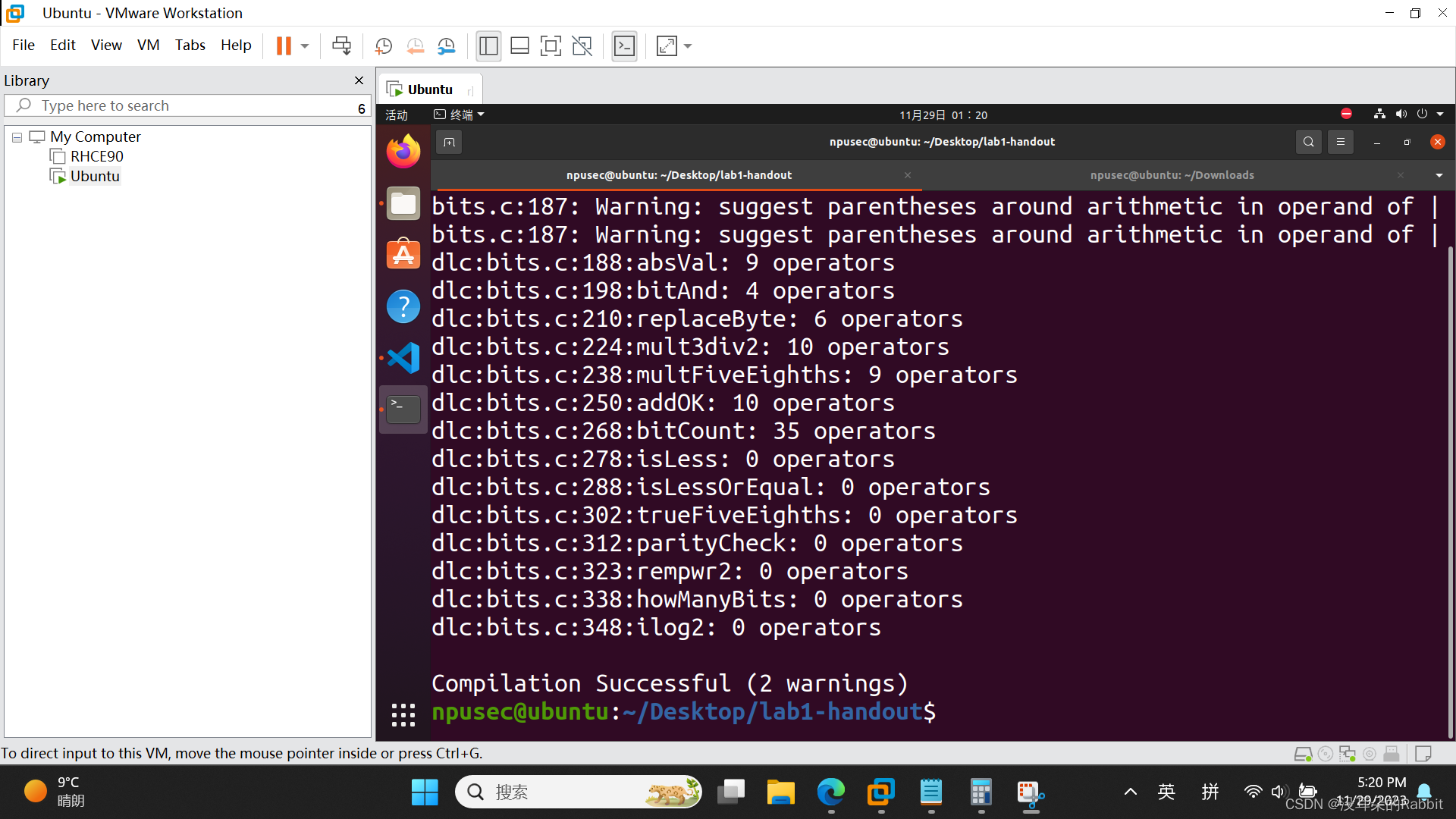
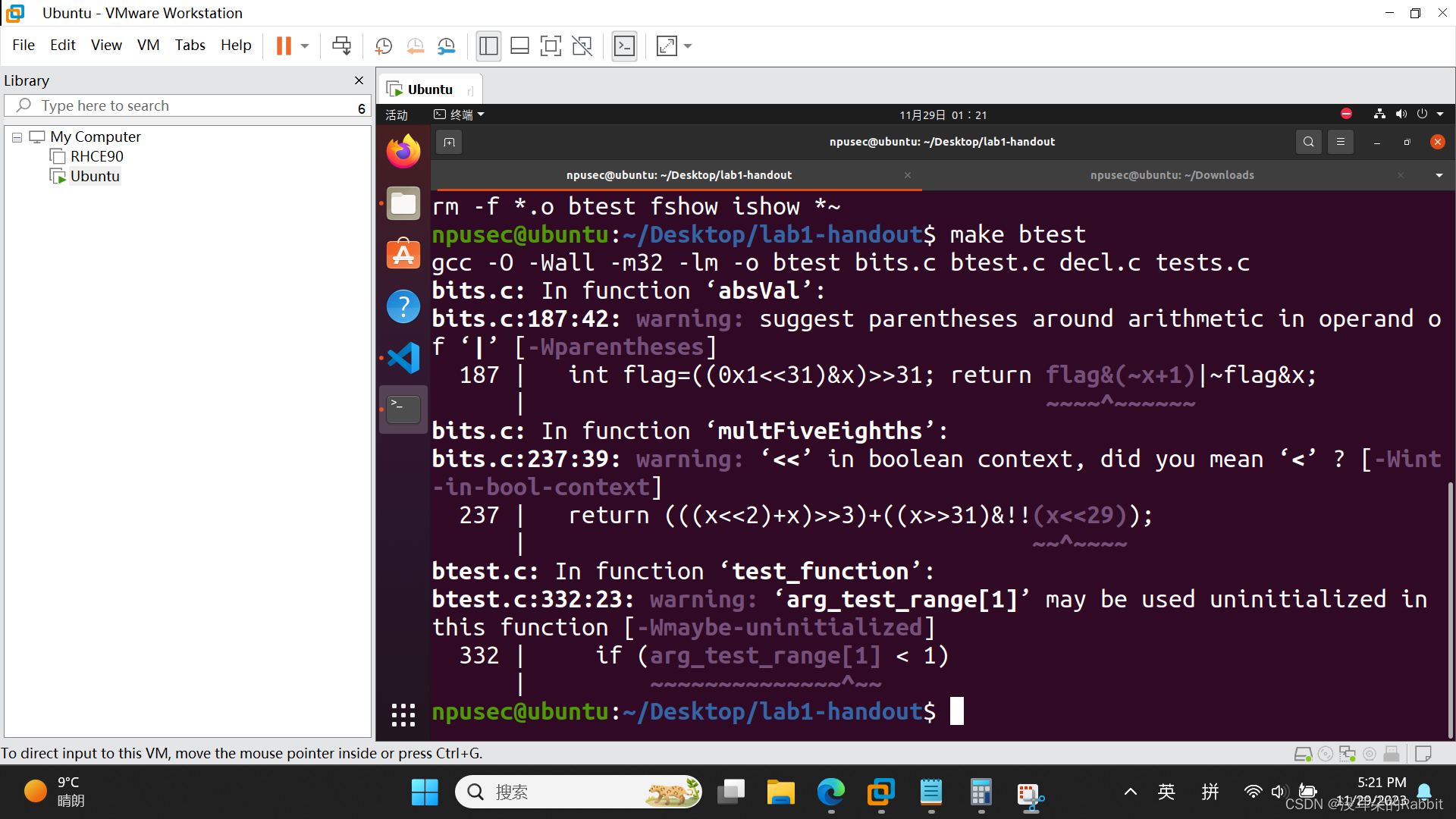
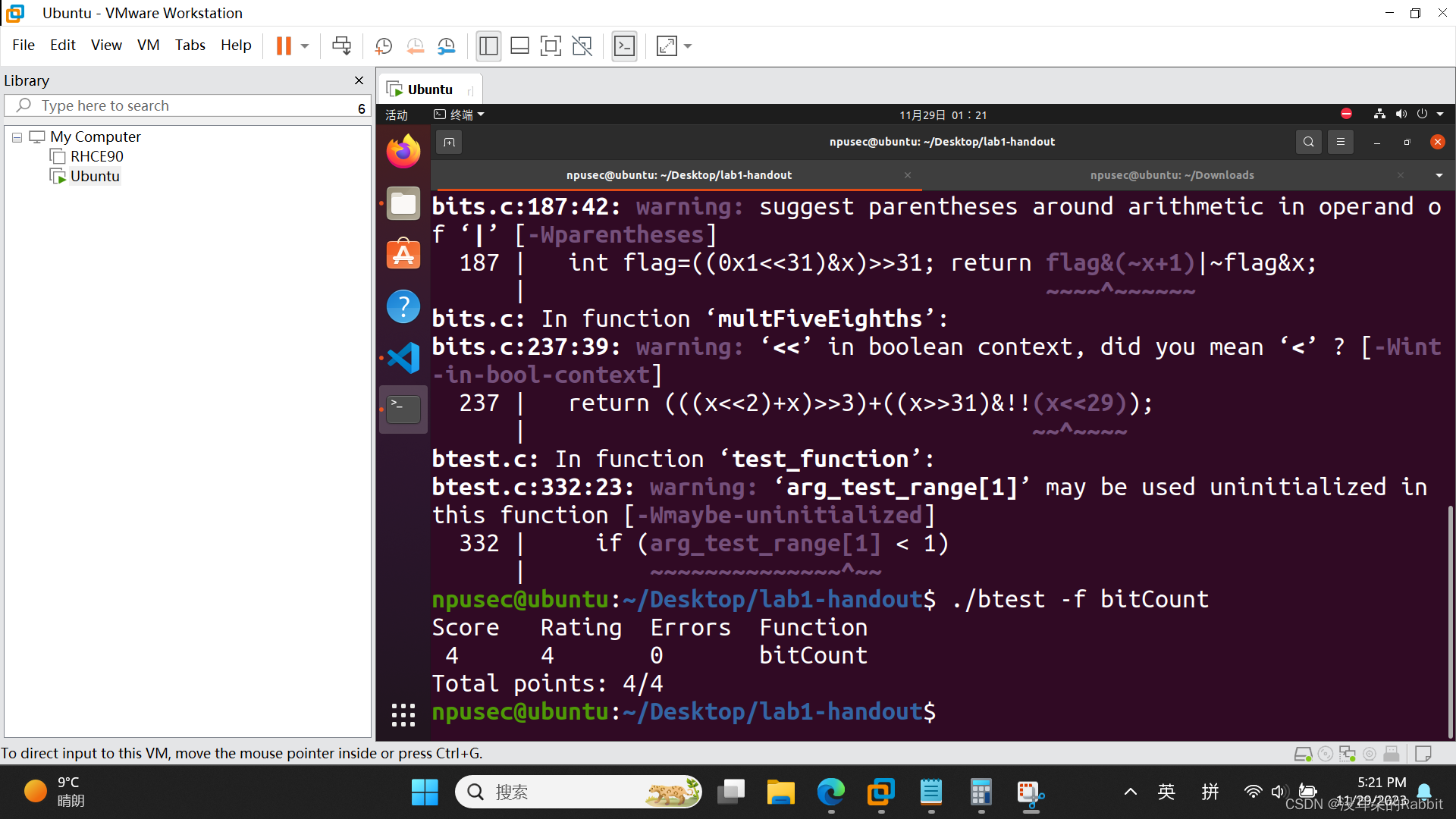
（图7：第8个函数）

**************************************************************************************************************

最后，45678这8个函数的代码如（图8：5个函数的C语言源代码）所示：

**************************************************************************************************************

int replaceByte(int x, int n, int c) {int temp = n<<3; return (c<<temp)|(~(0xFF<<temp)&x);
}
int mult3div2(int x) {int temp=(x<<1)+x; return (temp>>1)+(~(((temp<<31)&temp&x)>>31)+1);
}
int multFiveEighths(int x) {return (((x<<2)+x)>>3)+((x>>31)&!!(x<<29));
}
int addOK(int x, int y) {int sum=x+y;return !((~((x>>31)^(y>>31)))&((x>>31)^(sum>>31)));
}
int bitCount(int x) {int temp1 = 0x55|(0x55<<8)|(0x55<<16)|(0x55<<24);int temp2 = 0x33|(0x33<<8)|(0x33<<16)|(0x33<<24);int temp3 = 0xf|(0xf<<8)|(0xf<<16)|(0xf<<24);int n = x + ~((x >> 1) & temp1) + 1;n = (n & temp2) + ((n >> 2) & temp2);n = (n + (n >> 4)) & temp3;n = n + (n >> 8);n = n + (n >> 16);return n & 0x3f;
}

（图8：5个函数的C语言源代码）

**************************************************************************************************************