一、前言
算法(Algorithm)是指用来操作数据、解决程序问题的一组方法。对于同一个问题,使用不同的算法,也许最终得到的结果是一样的,但在过程中消耗的资源和时间却会有很大的区别
衡量不同算法之间的优劣主要是通过时间和空间两个维度去考量:
- 时间维度:是指执行当前算法所消耗的时间,我们通常用「时间复杂度」来描述。
- 空间维度:是指执行当前算法需要占用多少内存空间,我们通常用「空间复杂度」来描述
通常会遇到一种情况,时间和空间维度不能够兼顾,需要在两者之间取得一个平衡点是我们需要考虑的
一个算法通常存在最好、平均、最坏三种情况,我们一般关注的是最坏情况
最坏情况是算法运行时间的上界,对于某些算法来说,最坏情况出现的比较频繁,也意味着平均情况和最坏情况一样差
二、时间复杂度
时间复杂度是指执行这个算法所需要的计算工作量,其复杂度反映了程序执行时间「随输入规模增长而增长的量级」,在很大程度上能很好地反映出算法的优劣与否
一个算法花费的时间与算法中语句的「执行次数成正比」,执行次数越多,花费的时间就越多
算法的复杂度通常用大O符号表述,定义为T(n) = O(f(n)),常见的时间复杂度有:O(1)常数型、O(log n)对数型、O(n)线性型、O(nlogn)线性对数型、O(n^2)平方型、O(n^3)立方型、O(n^k)k次方型、O(2^n)指数型,如下图所示:
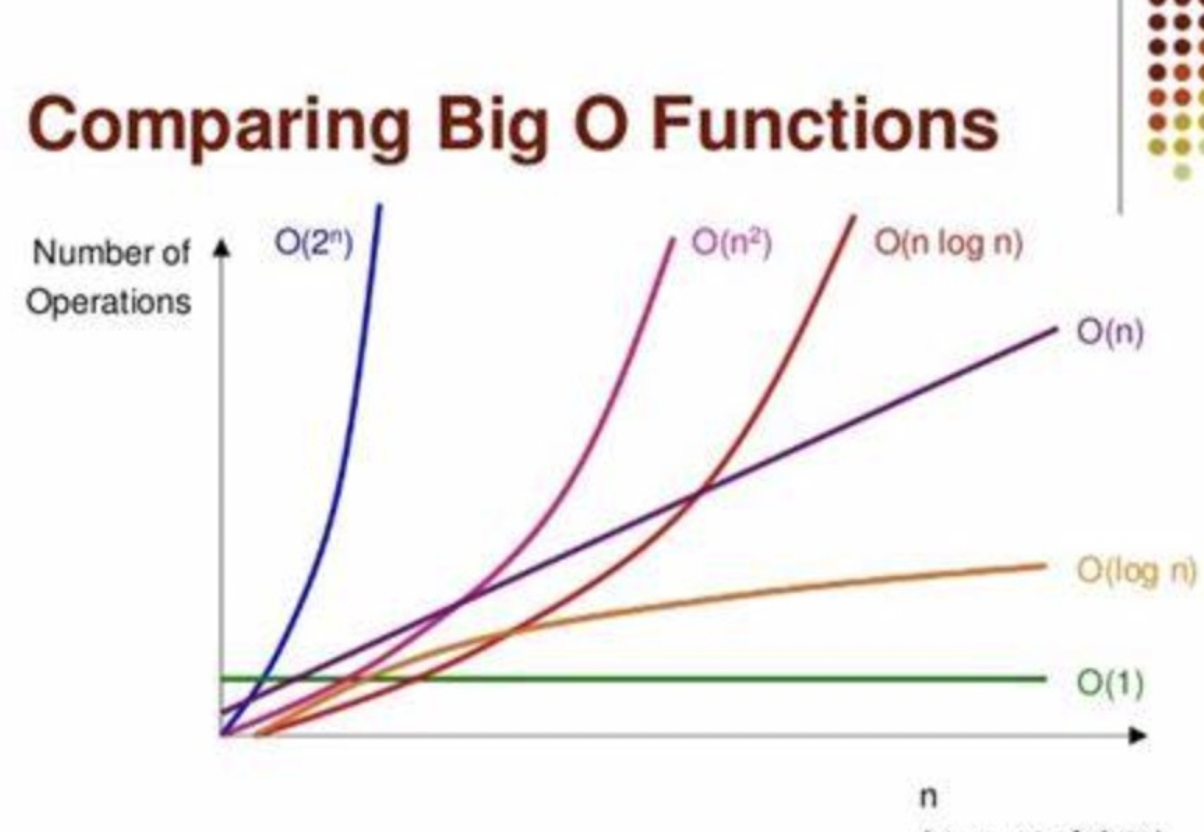
从上述可以看到,随着问题规模n的不断增大,上述时间复杂度不断增大,算法的执行效率越低,由小到大排序如下:
Ο(1)<Ο(log n)<Ο(n)<Ο(nlog n)<Ο(n2)<Ο(n3)<…<Ο(2^n)<Ο(n!)
注意的是,算法复杂度只是描述算法的增长趋势,并不能说一个算法一定比另外一个算法高效,如果常数项过大的时候也会导致算法的执行时间变长
关于如何计算时间复杂度,可以看看如下简单例子:
function process(n) {let a = 1let b = 2let sum = a + bfor(let i = 0; i < n; i++) {sum += i}return sum
}
该函数算法需要执行的运算次数用输入大小n的函数表示,即 T(n) = 2 + n + 1,那么时间复杂度为O(n + 3),又因为时间复杂度只关注最高数量级,且与之系数也没有关系,因此上述的时间复杂度为O(n)
又比如下面的例子:
function process(n) {let count = 0for(let i = 0; i < n; i++){for(let i = 0; i < n; i++){count += 1}}
}
循环里面嵌套循环,外面的循环执行一次,里面的循环执行n次,因此时间复杂度为 O(n*n*1 + 2) = O(n^2)
对于顺序执行的语句,总的时间复杂度等于其中最大的时间复杂度,如下:
function process(n) {let sum = 0for(let i = 0; i < n; i++) {sum += i}for(let i = 0; i < n; i++){for(let i = 0; i < n; i++){sum += 1}}return sum
}
上述第一部分复杂度为O(n),第二部分复杂度为O(n^2),总复杂度为max(O(n^2), O(n)) = O(n^2)
又如下一个例子:
function process(n) {let i = 1; // ①while (i <= n) {i = i * 2; // ②}
}
循环语句中以2的倍数来逼近n,每次都乘以2。如果用公式表示就是1 * 2 * 2 * 2 … * 2 <=n,也就是说2的x次方小于等于n时会执行循环体,记作2^x <= n,于是得出x<=logn
因此循环在执行logn次之后,便结束,因此时间复杂度为O(logn)
同理,如果一个O(n)循环里面嵌套O(logn)的循环,则时间复杂度为O(nlogn),像O(n^3)无非也就是嵌套了三层O(n)循环
三、空间复杂度
空间复杂度主要指执行算法所需内存的大小,用于对程序运行过程中所需要的临时存储空间的度量
除了需要存储空间、指令、常数、变量和输入数据外,还包括对数据进行操作的工作单元和存储计算所需信息的辅助空间
下面给出空间复杂度为O(1)的示例,如下
let a = 1
let b = 2
let c = 3
上述代码的临时空间不会随着n的变化而变化,因此空间复杂度为O(1)
let arr []
for(i=1; i<=n; ++i){arr.push(i)
}
上述可以看到,随着n的增加,数组的占用的内存空间越大
通常来说,只要算法不涉及到动态分配的空间,以及递归、栈所需的空间,空间复杂度通常为O(1),一个一维数组a[n],空间复杂度O(n),二维数组为O(n^2)