一、概念
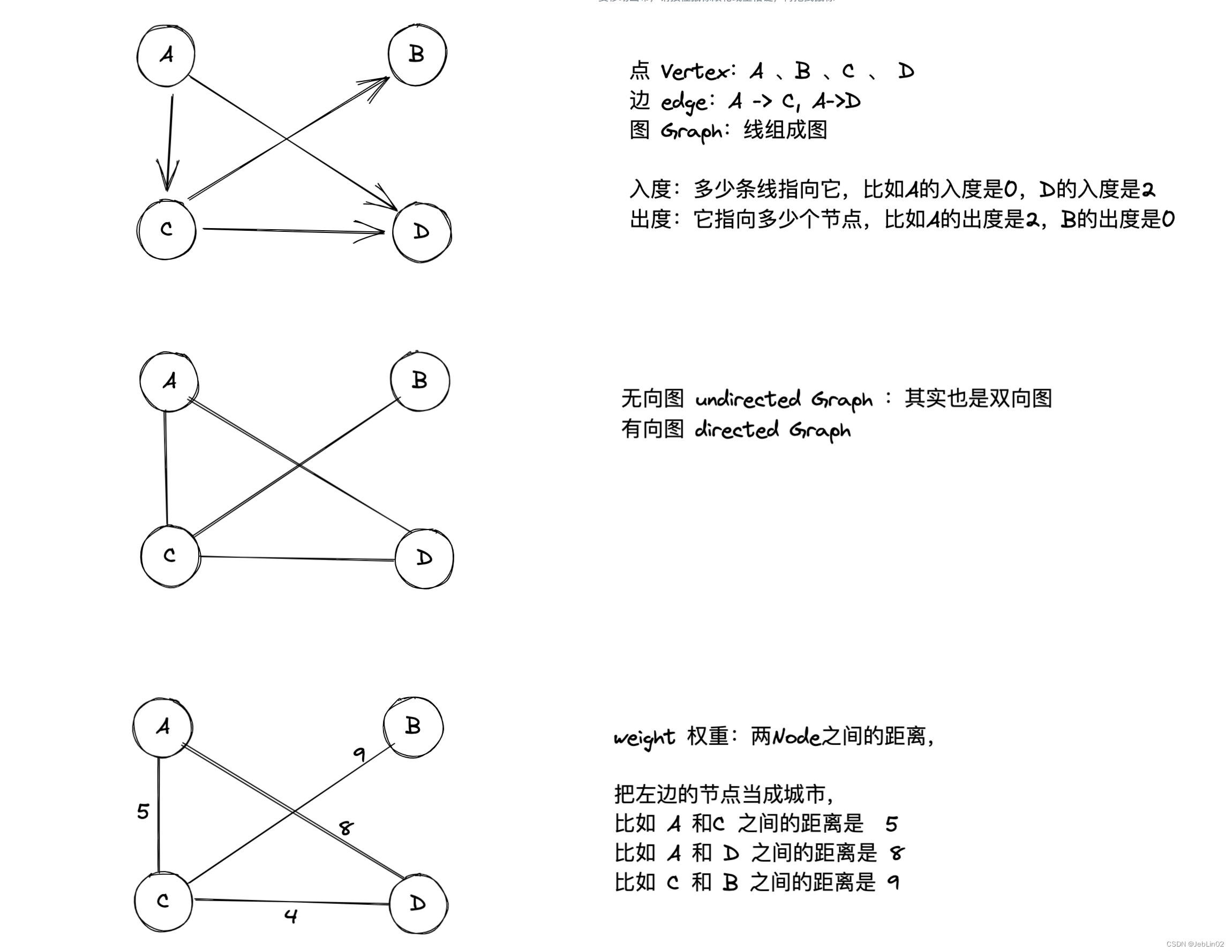
和二叉树的区别:图可能有环
常见概念
- 顶点(Vertex): 图中的节点或点。
- 边(Edge): 顶点之间的连接线,描述节点之间的关系。
- 有向图(Directed Graph): 边具有方向性的图,边有箭头表示方向。
- 无向图(Undirected Graph): 边没有方向性的图。
- 路径(Path): 顶点序列,通过边连接的顶点序列。
- 回路(Cycle): 闭合的路径,起点和终点相同的路径。
- 连通图(Connected Graph): 图中任意两个顶点之间都存在路径的图。
- 强连通图(Strongly Connected Graph): 有向图中任意两个顶点之间都存在双向路径的图。
- 连通分量(Connected Component): 无向图中的极大连通子图。
- 树(Tree): 无环连通图,任意两个节点都有唯一路径。
- 森林(Forest): 多个不相交树的集合。
- 度(Degree): 顶点的度是指与该顶点相关联的边的数量。
- 权重(Weight): 边或者顶点上的数值,表示边的代价或者顶点的属性。
邻接矩阵
| A | B | C | D | |
| A | 0 | 正无穷 | 5 | 8 |
| B | 正无穷 | 0 | 9 | 正无穷 |
| C | 5 | 9 | 0 | 4 |
| D | 8 | 正无穷 | 4 | 0 |
邻接表法
| Node | weight | |
| A | C | 5 |
| A | D | 8 |
| C | B | 9 |
| C | D | 4 |
| B | C | 9 |
| D | A | 8 |
| D | C | 4 |
二、算法题
1、套路模板
/*** @author jeb_lin* 22:27 2023/11/29*/
public class Node {public int value; // 可以改成 Stringpublic int in;// 入度public int out;// 出度public ArrayList<Node> nexts; // 多个后继节点public ArrayList<Edge> edges; // 多条边,该节点指出去的public Node(int value){this.value = value;this.in = 0;this.out = 0;this.nexts = new ArrayList<>();this.edges = new ArrayList<>();}public int getValue() {return value;}public void setValue(int value) {this.value = value;}public int getIn() {return in;}public void setIn(int in) {this.in = in;}public int getOut() {return out;}public void setOut(int out) {this.out = out;}public ArrayList<Node> getNexts() {return nexts;}public void setNexts(ArrayList<Node> nexts) {this.nexts = nexts;}public ArrayList<Edge> getEdges() {return edges;}public void setEdges(ArrayList<Edge> edges) {this.edges = edges;}
}
/*** @author jeb_lin* 22:27 2023/11/29*/
public class Edge {public Node from;public Node to;public int weight;public Edge(Node from, Node to, int weight) {this.weight = weight;this.from = from;this.to = to;}// 复写下面这俩,是为了放入Set的时候能正确去重@Overridepublic boolean equals(Object obj) {if (this == obj) {return true;}if (obj == null || !(obj instanceof Edge)) {return false;}Edge edge = (Edge) obj;return this.weight == edge.weight && Objects.equals(edge.from, this.from) && Objects.equals(edge.to, this.to);}@Overridepublic int hashCode() {return this.weight * this.from.hashCode() * this.to.hashCode();}public Node getFrom() {return from;}public void setFrom(Node from) {this.from = from;}public Node getTo() {return to;}public void setTo(Node to) {this.to = to;}public int getWeight() {return weight;}public void setWeight(int weight) {this.weight = weight;}
}
/*** @author jeb_lin* 22:26 2023/11/29*/
public class Graph {public HashMap<Integer,Node> nodes; // 该图上面的所有Node,nodeVal -> Nodepublic HashSet<Edge> edges; // 该图上面的所有边public Graph(){this.nodes = new HashMap<>();this.edges = new HashSet<>();}public HashMap<Integer, Node> getNodes() {return nodes;}public void setNodes(HashMap<Integer, Node> nodes) {this.nodes = nodes;}public HashSet<Edge> getEdges() {return edges;}public void setEdges(HashSet<Edge> edges) {this.edges = edges;}
}
2、二维数组转化成图
| 0 | 1 | 2 | 备注 | |
| 0 | 0 | 1 | 5 | Node0->Node1 ,weight=5 |
| 1 | 1 | 2 | 3 | Node1->Node2 ,weight=3 |
| 2 | 0 | 2 | 7 | Node0->Node2 ,weight=7 |
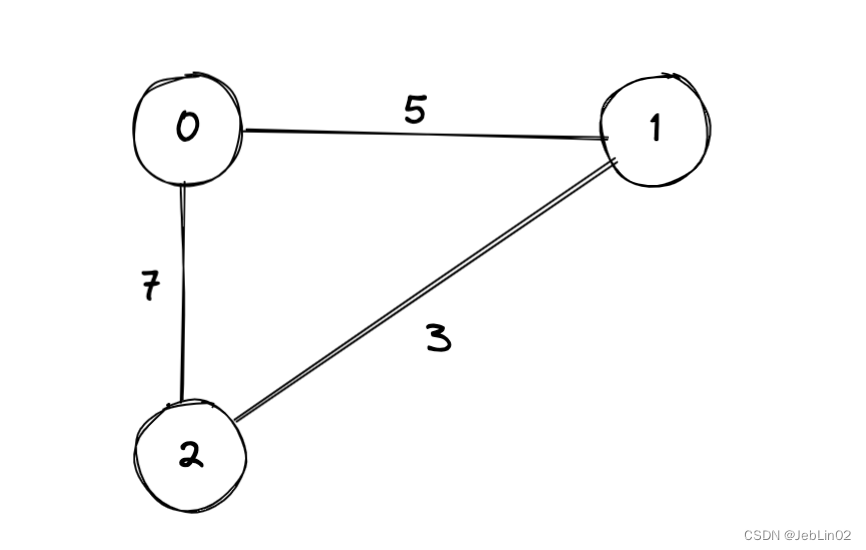
/*** 把二维数组转换成图* [* [0,1,5], // 表示 node0 -> node1 ,weight = 5* [1,2,3],* [0,2,7]* ]** @param matrix* @return*/public static Graph createGraph(int[][] matrix) {Graph graph = new Graph();HashMap<Integer, Node> nodes = new HashMap<>(); // 该图上面的所有Node,nodeVal -> NodeHashSet<Edge> edges = new HashSet<>(); // 该图上面的所有边graph.setEdges(edges);graph.setNodes(nodes);for (int i = 0; i < matrix.length; i++) {int[] row = matrix[i];if (!nodes.containsKey(row[0])) {nodes.put(row[0], new Node(row[0]));}if (!nodes.containsKey(row[1])) {nodes.put(row[1], new Node(row[1]));}Node from = nodes.get(row[0]);Node to = nodes.get(row[1]);from.setOut(from.getOut() + 1);to.setIn(to.getIn() + 1);from.getNexts().add(to);Edge edgeTemp = new Edge(from, to, row[2]);from.getEdges().add(edgeTemp);if(!edges.contains(edgeTemp)){edges.add(edgeTemp);}}return graph;}public static void main(String[] args) {int[][] arr = {{0, 1, 5}, {1, 2, 3}, {0, 2, 7}};Graph graph = createGraph(arr);System.out.println("ok");}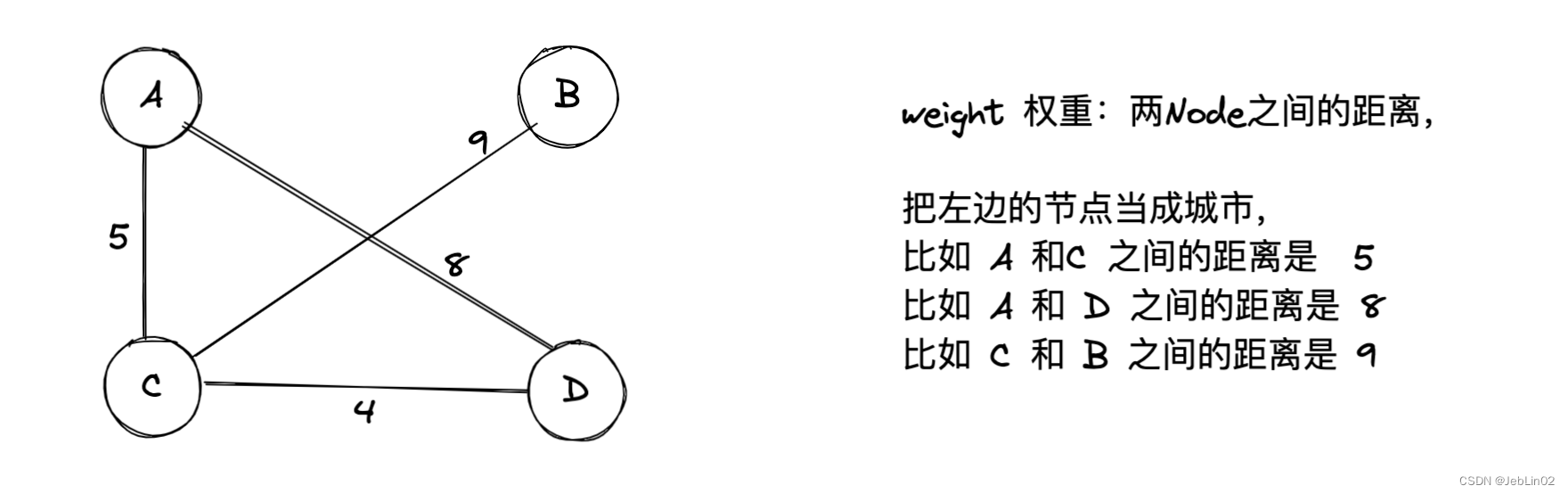
![[BJDCTF2020]The mystery of ip1](https://img-blog.csdnimg.cn/655cfbc9a0c64a218102a0a0443e1565.png)