考虑一个二分问题,即将实例分成正类(positive)或负类(negative)。对一个二分问题来说,会出现四种情况。如果一个实例是正类并且也被 预测成正类,即为真正类(True positive),如果实例是负类被预测成正类,称之为假正类(False positive)。相应地,如果实例是负类被预测成负类,称之为真负类(True negative),正类被预测成负类则为假负类(false negative)。
TP:正确肯定的数目;
FN:漏报,没有正确找到的匹配的数目;
FP:误报,给出的匹配是不正确的;
TN:正确拒绝的非匹配对数;
列联表如下表所示,1代表正类,0代表负类:
| 预测1 | 预测0 | |
| 实际1 | True Positive(TP) | False Negative(FN) |
| 实际0 | False Positive(FP) | True Negative(TN) |
1. TPR、FPR&TNR
从列联表引入两个新名词。其一是真正类率(true positive rate ,TPR), 计算公式为
TPR = TP / (TP + FN)
刻画的是分类器所识别出的 正实例占所有正实例的比例。
另外一个是负正类率(false positive rate, FPR),计算公式为
FPR = FP / (FP+ TN)
计算的是分类器错认为正类的负实例占所有负实例的比例。
还有一个真负类率(True Negative Rate,TNR),也称为specificity,计算公式为
TNR = TN /(FP+ TN) = 1 - FPR
2. 精确率Precision、召回率Recall和F1值
精确率(正确率)和召回率是广泛用于信息检索和统计学分类领域的两个度量值,用来评价结果的质量。其中精度是检索出相关文档数与检索出的文档总数的比率,衡量的是检索系统的查准率;召回率是指检索出的相关文档数和文档库中所有的相关文档数的比率,衡量的是检索系统的查全率。
一般来说,Precision就是检索出来的条目(比如:文档、网页等)有多少是准确的,Recall就是所有准确的条目有多少被检索出来了,两者的定义分别如下:
Precision = 提取出的正确信息条数 / 提取出的信息条数
Recall = 提取出的正确信息条数 / 样本中的信息条数
为了能够评价不同算法的优劣,在Precision和Recall的基础上提出了F1值的概念,来对Precision和Recall进行整体评价。F1的定义如下:
F1值 = 正确率 * 召回率 * 2 / (正确率+ 召回率)
不妨举这样一个例子:
某池塘有1400条鲤鱼,300只虾,300只鳖。现在以捕鲤鱼为目的。撒一大网,逮着了700条鲤鱼,200只虾,100只鳖。那么,这些指标分别如下:
正确率 = 700 / (700+ 200+100) = 70%
召回率 = 700 / 1400 = 50%
F1值 = 70% * 50% * 2 / (70%+50%) = 58.3%
不妨看看如果把池子里的所有的鲤鱼、虾和鳖都一网打尽,这些指标又有何变化:
正确率 = 1400 / (1400+ 300+ 300) = 70%
召回率 = 1400 / 1400 = 100%
F1值 = 70% * 100% * 2 / (70%+ 100%) = 82.35%
由此可见,正确率是评估捕获的成果中目标成果所占得比例;召回率,顾名思义,就是从关注领域中,召回目标类别的比例;而F值,则是综合这二者指标的评估指标,用于综合反映整体的指标。
当然希望检索结果Precision越高越好,同时Recall也越高越好,但事实上这两者在某些情况下有矛盾的。比如极端情况下,我们只搜索出了一个结果,且是准确的,那么Precision就是100%,但是Recall就很低;而如果我们把所有结果都返回,那么比如Recall是100%,但是Precision就会很低。因此在不同的场合中需要自己判断希望Precision比较高或是Recall比较高。如果是做实验研究,可以绘制Precision-Recall曲线来帮助分析。
3. 综合评价指标F-measure
Precision和Recall指标有时候会出现的矛盾的情况,这样就需要综合考虑他们,最常见的方法就是F-Measure(又称为F-Score)。
F-Measure是Precision和Recall加权调和平均:
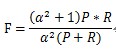
当参数α=1时,就是最常见的F1。因此,F1综合了P和R的结果,当F1较高时则能说明试验方法比较有效。
4. ROC曲线和AUC
4.1 为什么引入ROC曲线?
Motivation1:在一个二分类模型中,对于所得到的连续结果,假设已确定一个阀值,比如说 0.6,大于这个值的实例划归为正类,小于这个值则划到负类中。如果减小阀值,减到0.5,固然能识别出更多的正类,也就是提高了识别出的正例占所有正例 的比类,即TPR,但同时也将更多的负实例当作了正实例,即提高了FPR。为了形象化这一变化,引入ROC,ROC曲线可以用于评价一个分类器。
Motivation2:在类不平衡的情况下,如正样本90个,负样本10个,直接把所有样本分类为正样本,得到识别率为90%。但这显然是没有意义的。单纯根据Precision和Recall来衡量算法的优劣已经不能表征这种病态问题。
4.2 什么是ROC曲线?
ROC(Receiver Operating Characteristic)翻译为"接受者操作特性曲线"。曲线由两个变量1-specificity 和 Sensitivity绘制. 1-specificity=FPR,即负正类率。Sensitivity即是真正类率,TPR(True positive rate),反映了正类覆盖程度。这个组合以1-specificity对sensitivity,即是以代价(costs)对收益(benefits)。
此外,ROC曲线还可以用来计算“均值平均精度”(mean average precision),这是当你通过改变阈值来选择最好的结果时所得到的平均精度(PPV)。
为了更好地理解ROC曲线,我们使用具体的实例来说明:
如在医学诊断中,判断有病的样本。那么尽量把有病的揪出来是主要任务,也就是第一个指标TPR,要越高越好。而把没病的样本误诊为有病的,也就是第二个指标FPR,要越低越好。
不难发现,这两个指标之间是相互制约的。如果某个医生对于有病的症状比较敏感,稍微的小症状都判断为有病,那么他的第一个指标应该会很高,但是第二个指标也就相应地变高。最极端的情况下,他把所有的样本都看做有病,那么第一个指标达到1,第二个指标也为1。
我们以FPR为横轴,TPR为纵轴,得到如下ROC空间。
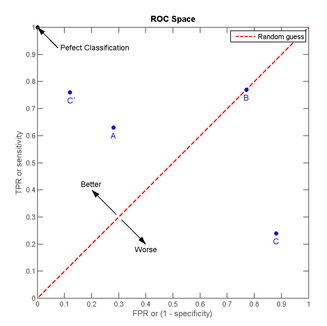
我们可以看出,左上角的点(TPR=1,FPR=0),为完美分类,也就是这个医生医术高明,诊断全对。点A(TPR>FPR),医生A的判断大体是正确的。中线上的点B(TPR=FPR),也就是医生B全都是蒙的,蒙对一半,蒙错一半;下半平面的点C(TPR<FPR),这个医生说你有病,那么你很可能没有病,医生C的话我们要反着听,为真庸医。上图中一个阈值,得到一个点。现在我们需要一个独立于阈值的评价指标来衡量这个医生的医术如何,也就是遍历所有的阈值,得到ROC曲线。
还是一开始的那幅图,假设如下就是某个医生的诊断统计图,直线代表阈值。我们遍历所有的阈值,能够在ROC平面上得到如下的ROC曲线。
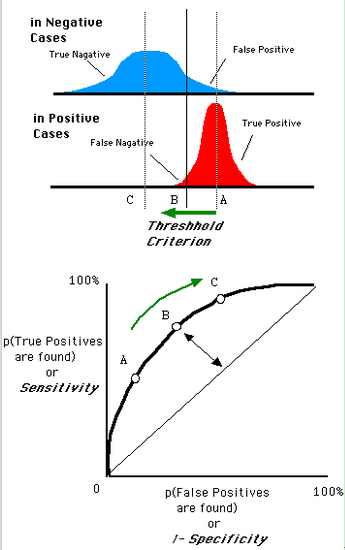
曲线距离左上角越近,证明分类器效果越好。
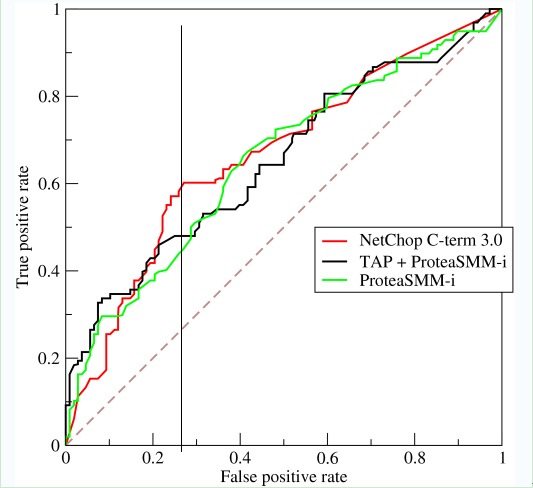
如上,是三条ROC曲线,在0.23处取一条直线。那么,在同样的低FPR=0.23的情况下,红色分类器得到更高的PTR。也就表明,ROC越往上,分类器效果越好。我们用一个标量值AUC来量化它。
4.3 什么是AUC?
AUC值为ROC曲线所覆盖的区域面积,显然,AUC越大,分类器分类效果越好。
AUC = 1,是完美分类器,采用这个预测模型时,不管设定什么阈值都能得出完美预测。绝大多数预测的场合,不存在完美分类器。
0.5 < AUC < 1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
AUC = 0.5,跟随机猜测一样(例:丢铜板),模型没有预测价值。
AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测。
AUC的物理意义:假设分类器的输出是样本属于正类的socre(置信度),则AUC的物理意义为,任取一对(正、负)样本,正样本的score大于负样本的score的概率。
4.4 怎样计算AUC?
第一种方法:AUC为ROC曲线下的面积,那我们直接计算面积可得。面积为一个个小的梯形面积之和。计算的精度与阈值的精度有关。
第二种方法:根据AUC的物理意义,我们计算正样本score大于负样本的score的概率。取NM(N为正样本数,M为负样本数)个二元组,比较score,最后得到AUC。时间复杂度为O(NM)。
第三种方法:与第二种方法相似,直接计算正样本score大于负样本的概率。我们首先把所有样本按照score排序,依次用rank表示他们,如最大score的样本,rank=n(n=N M),其次为n-1。那么对于正样本中rank最大的样本,rank_max,有M-1个其他正样本比他score小,那么就有(rank_max-1)-(M-1)个负样本比他score小。其次为(rank_second-1)-(M-2)。最后我们得到正样本大于负样本的概率为
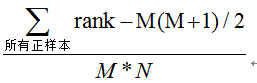
时间复杂度为O(N+M)。