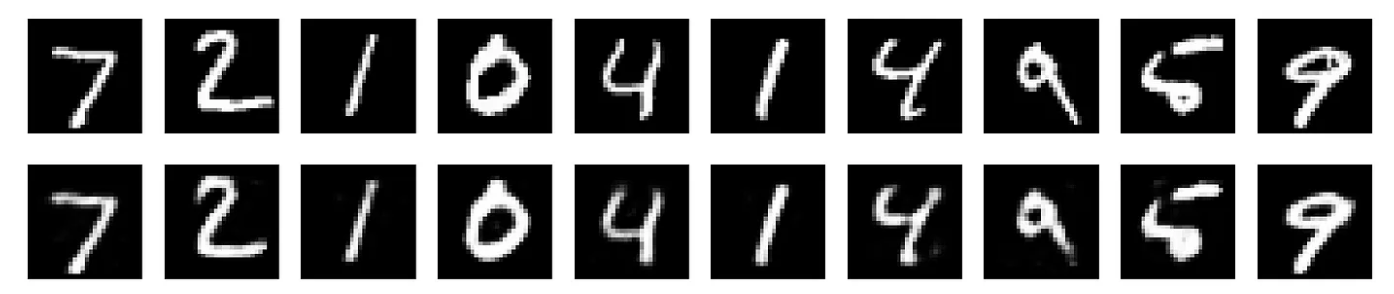前言

Textlive版本：2023

textstudio版本：4.6.3

名字和日期在以下地方修改:

图片下载地址;

figures.zip · LiangCha_Xyy/Source - Gitee.com

如下图，.tex文件和figures文件夹放在同一路径下即可

 .tex代码

\documentclass[UTF8]{ctexart}
\usepackage{listings}
\usepackage{xcolor} 
\usepackage{booktabs} %绘制表格
\usepackage{caption2} %标题居中
\usepackage{geometry}
\usepackage{amsmath}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{subfigure} 
\usepackage{longtable}
\usepackage{float}
\usepackage{graphicx}
\usepackage{booktabs}
\usepackage{indentfirst} 
\usepackage{setspace}
\usepackage{adjustbox}\graphicspath{{figures/}}
\geometry{a4paper,left=2.5cm,right=2.5cm,top=2.5cm,bottom=2.5cm}
\setlength{\parindent}{0em} 
\lstset{numbers=left, %设置行号位置numberstyle=\tiny, %设置行号大小keywordstyle=\color{blue}, %设置关键字颜色commentstyle=\color[cmyk]{1,0,1,0}, %设置注释颜色escapeinside=``, %逃逸字符(1左面的键)，用于显示中文%breaklines, %自动折行extendedchars=false, %解决代码跨页时，章节标题，页眉等汉字不显示的问题xleftmargin=1em,xrightmargin=1em, aboveskip=1em, %设置边距tabsize=4, %设置tab空格数showspaces=false %不显示空格
}
\title{	}
\author{自己的名字}
\renewcommand{\thesubsection}{\thesection.\arabic{subsection}}\begin{document}\begin{titlepage}\centering\vspace*{4cm} % 调整标题与图片的垂直间距\includegraphics[scale=0.08]{logo.png} \\{\Huge Beijing University of Chemical Technology\\} % 使用 \Huge 调整字体大小{\Huge Computing Methods\\ } \rule{15cm}{1.2pt}{\Huge\bfseries 计算方法课程实验\\}\rule{15cm}{1.2pt} \\[2cm] % 调整标题与作者信息之间的垂直间距{\Large 名字\\[1cm]} % 调整作者信息的垂直间距{\Large 日期\\}
\end{titlepage}
%实验二
\section{Lagrange插值方法}\subsection{实验目的}(1)熟悉简单的一阶和二阶 Lagrange插值方法；\\(2)学会计算 Lagrange基函数；\\(3)正确构造插值多项式；\\(4)对插值结果进行合理分析；\\\subsection{实验原理}$p_n(x)=\sum_{k=0}^n y_k l_k(x)=\sum_{k=0}^n\left(\prod_{\substack{j=0 \\ j \neq k}}^n \frac{x-x_j}{x_k-x_j}\right) y_k$ \\\subsection{实验环境}Windows 10 + Visual Studio\\\subsection{实验内容}\setstretch{1.5}\centering\begin{tabular}{|l|l|}\hline$x$ & $f(x)$ \\\hline 24 & 1.888175 \\26 & 1.918645 \\28 & 1.947294 \\30 & 1.961009 \\\hline\end{tabular} \\表 1.1: 数据样本表\\\vspace{0.5cm} % 插入垂直空白使用 Lagrange插值多项式计算 f(25),f(27),f(29)，并给出插值多项式。\\修改程序直至运行成功，查看运行结果，并和如下真实值进行比较。\\ \vspace{0.5cm} % 插入垂直空白\begin{tabular}{|l|l|}\hline$x$ & $f(x)$ \\\hline 25 & 1.90365393871587 \\27 & 1.933182044931763 \\29 & 1.961009057454548 \\\hline\end{tabular} \\表 1.2: 数据真实值\\\raggedright %左对齐\vspace{5cm} \subsection{程序代码}\begin{lstlisting}[language=C++,basicstyle=\small]
#include<iostream>
#include<cmath>
using namespace std;
int main()
{   //输入程序int m;cout<<"请输入有几个采样点："<<endl;cin>>m;pair<double,double> points[m];for(int i=0;i<m;i++){double x,y;cout<<"插值点：";cin>>x>>y;points[i] = {x,y};cout<<endl;}//程序处理int n;cout<<"请输入待预测的点的个数："<<endl;cin>>n;for(int i=0;i<n;i++){double x_pred;cin>>x_pred;double res = 0;for(int j=0;j<m;j++){ // 使用 m 而不是 ndouble a = 1, b = 1;for(int k=0;k<m;k++){ // 修改内层循环变量名为 kif(j!=k){a *= (x_pred - points[k].first);b *= (points[j].first - points[k].first);}}res += a * points[j].second / b;}cout<<"插值点：(x,y)=("<<x_pred<<","<<res<<")"<<endl;}
}\end{lstlisting}\vspace{5cm} 运行结果如下：\\\includegraphics[scale=0.8]{output1.png} \\%实验二
\section{牛顿插值方法}\subsection{实验目的}(1)理解牛顿插值方法；\\(2)学会计算差商；\\(3)正确构造插值多项式；\\(4)设计程序并调试得到正确结果；\subsection{实验原理}$f\left(x_0, x_1, \cdots, x_n\right)=\sum_{k=0}^n \frac{f\left(x_k\right)}{\prod_{\substack{j=0 \\ j \neq k}}^n\left(x_k-x_j\right)}$ \\$n$ 次插值多项式:\\$\begin{aligned}p_{n}(x) & =f\left(x_0\right)+f\left(x_0, x_1\right)\left(x-x_0\right)+f\left(x_0, x_1, x_2\right)\left(x-x_0\right)\left(x-x_1\right)+\cdots \\& +f\left(x_0, x_1, \cdots, x_n\right)\left(x-x_0\right)\left(x-x_1\right) \cdots\left(x-x_{n-1}\right)\end{aligned}$\subsection{实验环境}Windows 10 + Visual Studio\subsection{实验内容}计算以下积分值：\\\setstretch{1.5}\centering$$\begin{array}{|c|c|c|c|c|c|}\hline x & 0.4 & 0.55 & 0.65 & 0.8 & 0.9 \\\hline f(x) & 0.41075 & 0.57815 & 0.69675 & 0.88811 & 1.02652 \\\hline\end{array}$$\raggedright %左对齐\subsection{程序代码}\begin{lstlisting}[language=C++,basicstyle=\small]
#include<iostream>
#include<cmath>
using namespace std;
const int N = 4;//插值点数-1
pair<double,double>points[]={{0.4,0.41075},{0.55,0.57815},
{0.65,0.69675},{0.8,0.88811},{0.9,1.02652}};
//差商计算 + 数据点更新
void func(int n)
{double f[n];//差商表for(int k=1;k<=n;k++){f[0] = points[k].second;for(int i=0;i<k;i++) f[i+1] = (f[i]-points[i].second)/(points[k].first-points[i].first);points[k].second = f[k];}
}
int main()
{   double x = 0.895;double b = 0;func(N);for(int i=N-1;i>=0;i--){b = b*(x-points[i].first)+points[i].second;cout<<b<<endl;}cout<<"Nn("<<x<<")="<<b<<endl;}\end{lstlisting}运行结果如下：\\\includegraphics[scale=1]{output2.png} \\\vspace{5cm} \section{Newton-Cotes方法}\subsection{实验目的}(1)掌握Newton-Cotes算法；\\(2)要求程序不断加密对积分区间的等分,自动地控制Newton-Cotes算法中的加速收敛过程；\\(3)编写程序，分析实验结果；\subsection{实验原理}设将求积区间 $[a, b]$ 划分为 $n$ 等分, 选取等分点$$x_i=a+i h, \quad h=\frac{b-a}{n}, \quad i=0,1,2, \cdots, n$$作为求积节点构造求积公式$$\int_a^b f(x) d x \approx(b-a) \sum_{i=0}^n \lambda_i f\left(x_i\right)$$\subsection{实验环境}Windows 10 + Visual Studio\subsection{实验内容}$\begin{aligned}& \mathrm{I}=\int_0^\frac{1}{4} \sqrt{4-sin^2x} d x \quad(I \approx 0.4987111175752327) \\& \mathrm{I}=\int_0^1 \frac{\sin x}{x} d x \quad(f(0)=1, \quad I \approx 0.9460831) \\& \mathrm{I}=\int_0^1 \frac{e^x}{4+x^2} d x \\& \mathrm{I}=\int_0^1 \frac{\ln (1+x)}{1+x^2} d x\end{aligned}$\subsection{程序代码}\begin{lstlisting}[language=C++,basicstyle=\small]
#include<iostream>
#include<cmath>
using namespace std;
#define MAXSIZE 7
long c[MAXSIZE][MAXSIZE+5] = {{2,1,1}, {6,1,4,1}, {8,1,3,3,1}, {90,7,32,12,32,7}, {288,19,75,50,50,75,19}, {840, 41,216,27,272,27,216,41}, {17280,751,3577,1323,2989,2989,1323,3577,751}};
double func(double x) //原函数
{return log(1+x)/(1+x*x);
}
int main()
{cout<<"计算3.4函数积分值"<<endl;double a,b;int n;cout<<"请输入积分边界：";cin>>a>>b;cout<<"请输入积分节点数：";cin>>n;double h = (b-a)/(n-1);double f[n],x[n];for(int i=0;i<n;i++){//计算积分节点纵坐标x[i] = a+i*h;f[i] = func(x[i]);}double integral = 0;//积分值for(int i=0;i<n;i++){integral += c[n-2][i+1]*func(x[i]);}integral *= (b-a)/c[n-2][0];printf("积分值为=%lf", integral);}\end{lstlisting}运行结果如下：\\\begin{figure}[ht]\centering\begin{adjustbox}{width=0.24\textwidth,height=2cm}\includegraphics{output31.png}\end{adjustbox}\begin{adjustbox}{width=0.24\textwidth,height=2cm}\includegraphics{output32.png}\end{adjustbox}\begin{adjustbox}{width=0.24\textwidth,height=2cm}\includegraphics{output33.png}\end{adjustbox}\begin{adjustbox}{width=0.24\textwidth,height=2cm}\includegraphics{output34.png}\end{adjustbox}\caption{计算函数积分值}\end{figure}\subsection{实验分析}\begin{figure}[ht]\centering\includegraphics[scale=0.42]{py.png}\caption{函数(3.1)的图像}\end{figure}应用 Newton-Cotes 公式得到近似积分值为：\\$$I = 0.498711$$积分精确值为 0.4987111175752327，由此可见两者是非常接近的\section{求非线性方程根的牛顿法}\subsection{实验目的}(1)掌握求非线性方程根的牛顿法；\\(2)进一步了解牛顿法的改进算法；\\(3)编写程序，分析实验结果；\subsection{实验原理}牛顿法迭代公式为：\\$$x_{k+1}=x_k-\frac{f\left(x_k\right)}{f'\left(x_k\right)}$$\subsection{实验环境}Windows 10 + Visual Studio\\\subsection{实验内容}用牛顿迭代法求$ xe^x − 1 = 0 $的根，迭代初始值为 $x_0 = 0.5。$\raggedright %左对齐\subsection{程序代码}\begin{lstlisting}[language=C++,basicstyle=\small]
#include<iostream>
#include<cmath>
using namespace std;
double f(double x)//原函数
{return x*exp(x)-1;
}
double df(double x)//导函数
{return exp(x) + x*exp(x);
}
int main()
{double x;double eplison;cout<<"请输入精度要求："<<endl;cin>>eplison;cout<<"请输入迭代初值："<<endl;cin>>x;double x0 = x;double x1 = x0 - f(x0)/df(x0);while(fabs(x1-x0)>eplison){double temp = x1;x1 = x0 - f(x0)/df(x0);x0 = temp;}cout<<"f(x)=0的根x="<<x1<<endl;}\end{lstlisting}运行结果如下：\\\includegraphics[scale=1]{output4.png} \\\section{解线性方程组的迭代法}\subsection{实验目的}(1) 掌握雅可比迭代和 Seidel 迭代来求解方程组；\\(2) 掌握常用的几种迭代格式；\\(3) 编写程序实现上述迭代方法；\\(4) 分析实验结果，并估计误差；\subsection{实验原理}有如下线性方程组 Ax = b 如下：\\$$\left(\begin{array}{cccc}a_{11} & a_{12} & \cdots & a_{1 n} \\a_{21} & a_{22} & \cdots & a_{2 n} \\\vdots & \vdots & \ddots & \vdots \\a_{n 1} & a_{n 2} & \cdots & a_{n n}\end{array}\right)\left(\begin{array}{c}x_1 \\x_2 \\\vdots \\x_n\end{array}\right)=\left(\begin{array}{c}b_1 \\b_2 \\\vdots \\b_n\end{array}\right)$$使用迭代法进行求解，主要迭代方法为雅可比迭代和 Gauss-Seidel 迭代\\\subsection{实验环境}Windows 10 + Visual Studio\\\subsection{实验内容}使用高斯-赛德尔迭代法求解下列方程组：\\$\left\{\begin{array}{l}10x_1 - x_2 - 2x_3 = 7.2 \\-x_1 + 10x_2 - 2x_3 = 8.3 \\-x_1 - x_2 + 5x_3 = 4.2 \\\end{array}\right. $\subsection{程序代码}\begin{lstlisting}[language=C++,basicstyle=\small]
#include <iostream>
using namespace std;
void input(int n, double b[], double **coefficient){cout<<"请输入系数矩阵："<<endl;for(int i=0;i<n;i++){for(int j=0;j<n;j++) cin>>coefficient[i][j];}cout<<"请输入常数矩阵：";for(int i=0;i<n;i++) cin>>b[i];
}
int main()
{int n;double epsilon;cout << "请输入未知数个数：";cin >> n;double b[n];double x0[n];double x1[n];double **coefficient = new double*[n];for (int i = 0; i < n; i++) {coefficient[i] = new double[n];}input(n, b, coefficient);cout<<"请输入迭代初值：";for(int i=0;i<n;i++) cin>>x0[i];cout<<"请输入精度要求：";cin>>epsilon;while(true){for(int i=0;i<n;i++){double res = 0;for(int j=0;j<=i-1;j++){res += coefficient[i][j]*x1[j];}for(int j=i+1;j<=n;j++){res += coefficient[i][j]*x0[j];}x1[i] = (b[i]-res)/coefficient[i][i];}if(abs(x1[0]-x0[0])<epsilon) break;for(int i=0;i<n;i++) x0[i] = x1[i];}cout<<"解为：";for(int i=0;i<n;i++) cout<<x1[i]<<" ";for (int i = 0; i < n; i++) {delete[] coefficient[i];}delete[] coefficient;return 0;
}\end{lstlisting}运行结果如下：\\\includegraphics[scale=1]{output5.png} \\\section{线性方程组的高斯消元法}\subsection{实验目的}(1) 掌握高斯消元法求解方程组；\\(2) 掌握列主元高斯消元法求解方程组；\\(3) 分析实验结果，并估计误差；\subsection{实验原理}有线性方程组 Ax = b \\$\left\{\begin{aligned}x_n & =\frac{b_n^{(n)}}{a_{n n}^{(n)}} \\x_i & =\frac{b_i^{(i)}-\sum_{j=i+1}^n a_{i j}^{(i)} x_j}{a_{i i}^{(i)}} \quad i=n-1, n-2, n-3, \cdots, 2,1\end{aligned}\right.$\subsection{实验环境}Windows 10 + Visual Studio\\\subsection{实验内容}使用高斯消元法求解下列方程组：\\$$\left\{\begin{array}{l}10 x_1-x_2-2 x_3=7.2 \\-x_1+10 x_2-2 x_3=8.3 \\-x_1-x_2+5 x_3=4.2\end{array}\right.$$\subsection{程序代码}\begin{lstlisting}[language=C++,basicstyle=\small]
#include <iostream>
using namespace std;
void input(int n, double b[], double **a){cout<<"请输入增广矩阵："<<endl;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++) cin>>a[i][j];cin>>b[i];}}
int main()
{int n;cout << "请输入未知数个数：";cin >> n;double b[n+1];double **a = new double*[n+1];for (int i = 0; i <=n; i++) {a[i] = new double[n+1];}input(n,b,a);for(int k=1;k<=n;k++){for(int j=k+1;j<=n;j++)a[k][j]/=a[k][k];//计算行乘子b[k]/=a[k][k];for(int i=k+1;i<=n;i++){for(int j=k+1;j<=n;j++){a[i][j]-=a[i][k]*a[k][j];}}for(int i=k+1;i<=n;i++) b[i]-=a[i][k]*b[k];}for(int i=n-1;i>=1;i--){double temp = 0;for(int j=i+1;j<=n;j++) temp+=a[i][j]*b[j];b[i] -= temp;}cout<<"解为：";for(int i=1;i<=n;i++) printf("%.4lf  ",b[i]);for (int i =0;i<=n; i++) {delete[] a[i];}delete[] a;return 0;
}\end{lstlisting}运行结果如下：\\\includegraphics[scale=1]{output6.png} \\\section{线性方程组的矩阵分解法}\subsection{实验目的}(1) 掌握采用矩阵 LU 分解方法来求解线性方程组；\\(2) 编程实现矩阵 LU 分解算法；\subsection{实验原理}矩阵的 LU 分解定理:\\设A为n阶方阵，如果A的顺序主子矩阵 $A_1, A_2, · · · , A_{n-1}$均非奇异，则A可分解为一个单位下三角矩阵L和一个上三角矩阵U的乘积，即A = LU，且这种分解是唯一的。\\其中 L 和 U 的计算公式为：\\$$\left\{\begin{array}{l}u_{1 j}=a_{1 j}, \quad j=1,2,3, \cdots, n \\l_{i 1}=\frac{a_{i 1}}{u_{11}}, \quad i=2,3,4, \cdots, n \\u_{i j}=a_{i j}-\sum_{k=1}^{i-1} l_{i k} u_{k j}, \quad j=i, i+1, \cdots, n \\l_{i j}=\frac{a_{i j}-\sum_{k=1}^{j-1} l_{k k} u_{k j}}{u_{j j}}, \quad j=1,2, \cdots, i-1\end{array}\right.$$\subsection{实验环境}Windows 10 + Visual Studio\\\subsection{实验内容}(1) 写出矩阵 LU 分解法解线性方程组算法，编一程序上机调试出结果，要求所编程序适用于任何一解线性方程组问题，即能解决这一类问题，而不是某一个问题。\\(2) 使用矩阵 Doolittle 分解法求解下列方程组：\\$$\left\{\begin{array}{l}10 x_1-x_2-2 x_3=7.2 \\-x_1+10 x_2-2 x_3=8.3 \\-x_1-x_2+5 x_3=4.2\end{array}\right.$$\subsection{程序代码}\begin{lstlisting}[language=C++,basicstyle=\small]
#include <iostream>
using namespace std;
void input(int n, double b[], double **a){cout<<"请输入增广矩阵："<<endl;for(int i=0;i<n;i++){for(int j=0;j<n;j++) cin>>a[i][j];cin>>b[i];}}
int main()
{int n;cout << "请输入未知数个数：";cin >> n;double b[n+1];double **a = new double*[n+1];for (int i = 0; i <=n; i++) {a[i] = new double[n+1];}double l[n+1][n+1],u[n+1][n+1];double x[n+1],y[n+1];input(n,b,a);for(int i=0;i<n;i++) l[i][i] = 1;//LU分解for(int k=0;k<n;k++){for(int j=k;j<n;j++){u[k][j] = a[k][j];for(int i=0;i<=k-1;i++){u[k][j] -= (l[k][i]*u[i][j]);}}for(int i=k+1;i<n;i++){l[i][k] = a[i][k];for(int j=0;j<=k-1;j++)l[i][k]-=(l[i][j]*u[j][k]);l[i][k]/=u[k][k];}}//Ly = bfor(int i=0;i<n;i++){y[i] = b[i];for(int j=0;j<=i-1;j++) y[i]-=(l[i][j]*y[j]);}//Ux = yfor(int i=n-1;i>=0;i--){x[i] = y[i];for(int j=i+1;j<n;j++) x[i]-=(u[i][j]*x[j]);x[i]/=u[i][i];}cout<<"L矩阵为："<<endl;for(int i=0;i<n;i++){for(int j=0;j<n;j++) printf("%7.4f ",l[i][j]);cout<<endl;}cout<<"U矩阵为："<<endl;for(int i=0;i<n;i++){for(int j=0;j<n;j++) printf("%7.4f ",u[i][j]);cout<<endl;}cout<<"解为：";for(int i=0;i<n;i++) printf("%.4lf  ",x[i]);for (int i =0;i<=n; i++) {delete[] a[i];}delete[] a;return 0;
}\end{lstlisting}运行结果如下：\\\includegraphics[scale=1]{output7.png} \\\section{常微分方程求解算法}\subsection{实验目的}(1) 掌握采用欧拉法来求解常微分方程；\\(2) 掌握采用改进的欧拉法来求解常微分方程；\\(3) 编程实现上述两个算法；\subsection{实验原理}由$$\left\{\begin{array}{l}y^{\prime}=f(x, y) \\y\left(x_0\right)=y_0\end{array}\right.$$可知$$y^{\prime}\left(x_n\right)=f\left(x_n, y\left(x_n\right)\right)$$用向前差商代替导数:$$y^{\prime}\left(x_n\right) \approx \frac{y\left(x_{n+1}\right)-y\left(x_n\right)}{h}$$代入上式得到:$$y\left(x_{n+1}\right) \approx y\left(x_n\right)+h f\left(x_n, y\left(x_n\right)\right)$$用 $y_n$ 作为 $y\left(x_n\right)$ 的近似值, 并将所得结果作为 $y_{n+1}$, 得到$$y_{n+1}=y_n+h f\left(x_n, y_n\right)$$将 $y_{n+1}$ 作为 $y\left(x_{n+1}\right)$ 的近似值, 由此得到 (向前)Euler 格式:$$\left\{\begin{array}{l}y_0=y\left(x_0\right) \\y_{n+1}=y_n+h f\left(x_n, y_n\right)\end{array}\right.$$初值 $y_0$ 是已知的, 则依据上式即可逐步算出微分方程初值问题的数值解 $y_1, y_2, y_3, \cdots, y_n, \cdots$ 。\subsection{实验环境}Windows 10 + Visual Studio\\\subsection{实验内容}(1) 写出欧拉法或改进的欧拉法来求解常微分方程，编程序上机调试出结果。\\(2) 使用常微分方程例子如下：$\left\{\begin{array}{l}y^{\prime}=3 x-2 y^2-1(0<x<5) \\ y(0)=2\end{array}\right.$\subsection{程序代码}\begin{lstlisting}[language=C++,caption={欧拉法},basicstyle=\small]
#include<iostream>
using namespace std;
double f(double x,double y){return 3*x-2*y*y-1;
}
int main()
{const double h = 0.25;double x = 0;double y = 2;int idx = 0;while(x<=5){idx++;cout<<"第"<<idx<<"轮：x:"<<x<<" y:"<<y<<endl;x += h;y = y+h*f(x,y);}
}\end{lstlisting}\begin{lstlisting}[language=C++,caption={改进欧拉法},basicstyle=\small]
#include<iostream>
using namespace std;
double f(double x,double y){return 3*x-2*y*y-1;
}
int main()
{const double h = 0.25;double x = 0;double y = 2;double _y;int idx = 0;while(x<=5){idx++;cout<<"第"<<idx<<"轮： x:"<<x<<" y:"<<y<<endl;_y = y+h*f(x,y);y = y+(h/2)*(f(x,y)+f(x+h,_y));x+=h;}
}\end{lstlisting}\vspace{5cm} 运行结果如下：\\\centering\includegraphics[scale=1]{output81.png} \\欧拉法\\\includegraphics[scale=0.87]{output82.png} \\改进欧拉法
\end{document}