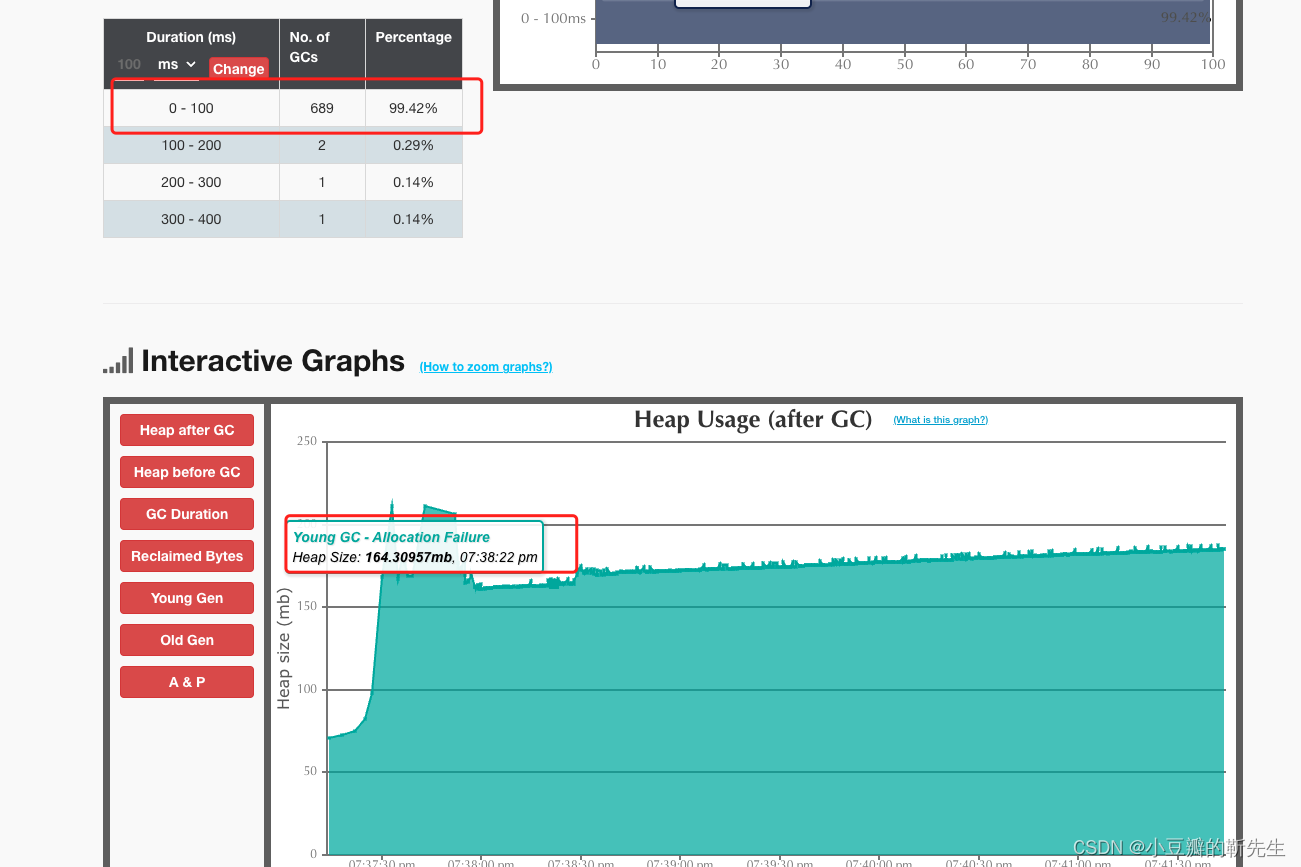
【题目来源】
https://www.acwing.com/problem/content/description/3435/
【题目描述】
如下图所示,由正整数 1, 2, 3, … 组成了一棵无限大的(满)二叉树。
1/ \2 3/ \ / \4 5 6 7
/\ /\ /\ /\
... ... 从任意一个结点到根结点(编号是 1 的结点)都有一条唯一的路径,比如从 5 到根结点的路径是 (5,2,1),从 4 到根结点的路径是 (4,2,1),从根结点 1 到根结点的路径上只包含一个结点 1,因此路径就是 (1)。
对于两个结点 x 和 y,假设他们到根结点的路径分别是 (x1,x2,…,1) 和 (y1,y2,…,1),那么必然存在两个正整数 i 和 j,使得从 xi 和 yj 开始,有 xi=yj,xi+1=yj+1,xi+2=yj+2,…
现在的问题就是,给定 x 和 y,要求他们的公共父结点,即 xi(也就是 yj)。
【数据范围】
1≤x, y≤2^31−1
【输入格式】
一行,两个整数,空格隔开,表示两个结点。
【输出格式】
一行,一个整数,表示公共结点。
【输入样例】
10 4
【输出样例】
2
【算法分析】
对于一个二叉树,定义当前节点的编号为 i(从 1 开始),那么它的左子节点为 2*i,右子节点是2*i+1。故寻找两个节点的公共父节点,可以让其分别除以2,直到两个节点指向同一个位置。
时间复杂度为。
【算法代码】
#include<bits/stdc++.h>
using namespace std;int x,y;
int main() {cin>>x>>y;while(true) {if(x>y) x/=2;else if(y>x) y/=2;else break;}cout<<x<<endl;return 0;
}/*
in:
10 4out:
2
*/
【参考文献】
https://blog.csdn.net/hnjzsyjyj/article/details/131620651
https://www.acwing.com/solution/content/126489/
https://www.acwing.com/solution/content/126493/