文档讲解:代码随想录
视频讲解:代码随想录B站账号
状态:看了视频题解和文章解析后做出来了
84.柱状图中最大的矩形
class Solution:def largestRectangleArea(self, heights: List[int]) -> int:heights.insert(0, 0)heights.append(0)stack = [0]result = 0for i in range(1, len(heights)):while stack and heights[i] < heights[stack[-1]]:mid_height = heights[stack[-1]]stack.pop()if stack:# area = width * heightarea = (i - stack[-1] - 1) * mid_heightresult = max(area, result)stack.append(i)return result- 时间复杂度:O(N)
- 空间复杂度:O(N)
和雨水那道题差不多,这道题的区别在于单调栈里的元素是栈头到栈尾从大到小,这样计算出最大的长方形面积。
只有栈里从大到小的顺序,才能保证栈顶元素找到左右两边第一个小于栈顶元素的柱子:
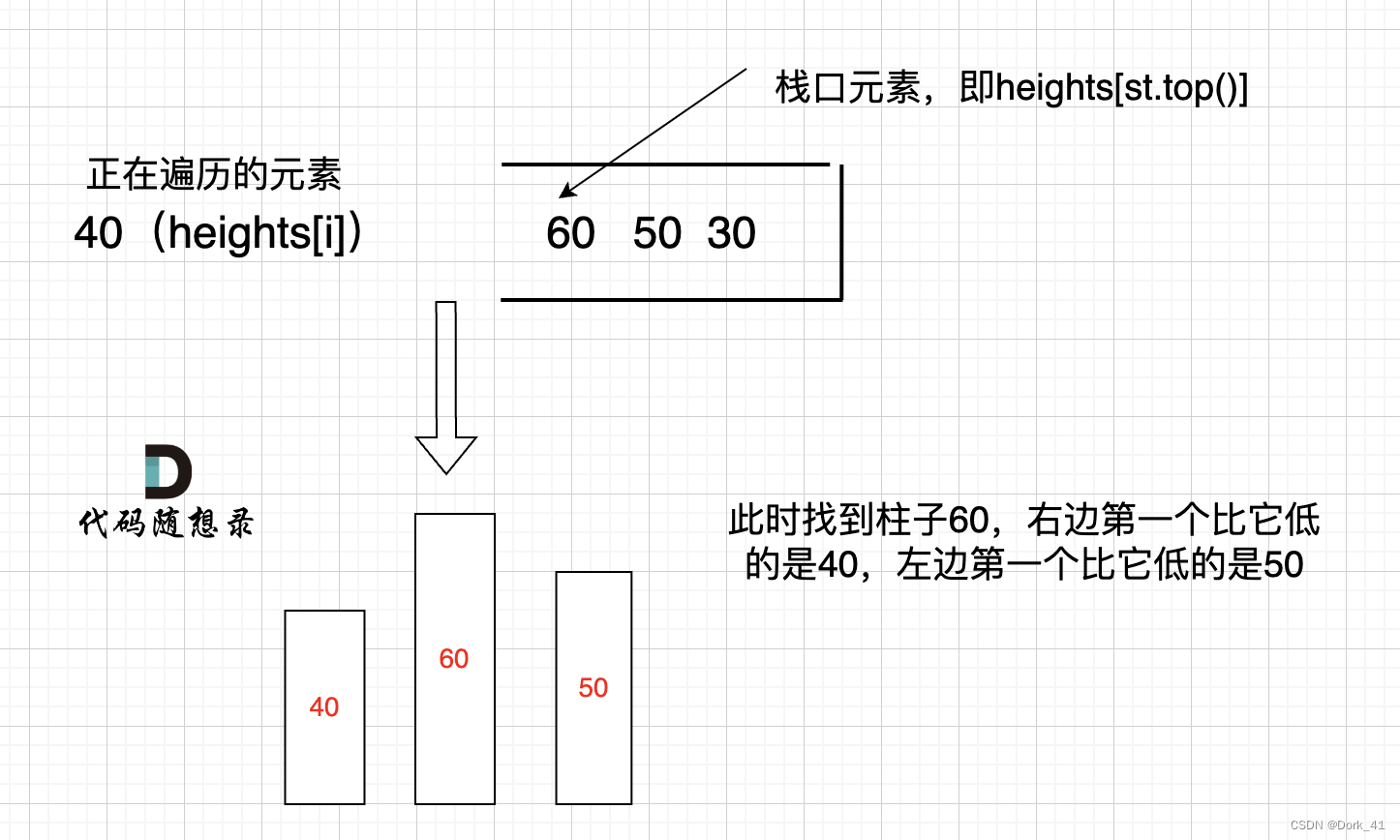
这道题还需要在input数组的头尾分别加上高度为0的bar,这样确保第一个出栈的元素可以计算到面积,以及如果单调栈里都是从大到小(这样就不会有出栈了)最后的0保证一定有出栈来计算面积。
其他的和接雨水差不多,都是先pop然后记录pop的值作为高度,当前元素减去栈顶的下标再减一作为宽度,这两个相乘并不断更新result来计算最大的长方形面积。
代码随想录刷题总结
虽然只有60天的刷题时间,但这段经历充满了曲折。从最初的激情到中途的疲惫,再到后来习惯的形成,如果没有这个训练营和陪我一起刷题的小伙伴,我可能还在每天挣扎刷题的阶段。
解决每一种题目的关键在于掌握它想考察的核心思想和解题的关键方法。以回溯法为例,虽然N皇后问题看起来很复杂,但只要掌握了回溯的基本步骤,明确每个环节,代码实现就顺其自然了。一种题型的解题方法常常可以启发解决其他题型,即使是难题,也不过是基础题型的变体而已。因此,从简单题开始逐步提升的策略也是非常有效的。
刷题时最忌讳的是对问题一知半解。我之前刷题时,一旦没思路就会看别人的解答,然后模仿搬过来,随意理解别人的思路,只要通过就认为完成了。这种方法是不可取的,因为解答只提供了大致的思路,无法涵盖所有细节和考虑。
代码中的每一个细节都可能是解题的关键。比如二分查找,for循环中的范围区间虽看似简单,实际上却是掌握这类题型的核心概念。再如动态规划中的背包问题,两个循环的顺序看似显而易见,但物品和背包的循环顺序,以及为什么有时候需要逆序循环,都是值得深入研究的。
我即将开始第二轮的刷题,希望这次能更加注重细节,争取做到对每一题的核心概念都有更加深入的理解。