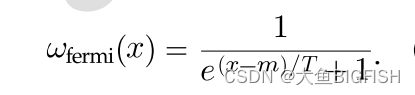前言
- 很荣幸参与到由“极术社区和全志在线联合组织”举办的XR806开发板试用活动。
- 本人热衷于各种的开发板的开发,同时更愿意将其实现到具体项目中。
- 秉承以上原则,发现大家的重心都放在开发中的环境构建过程,缺少了不少实际应用场景的运用,虽然环境搭建确实痛苦。本文主要使用XR806的FreeRTOS到实际的机器人控制应用中,并实现部署模糊控制器。
- 环境搭建本文简要略写,大家可以看社区其它优秀的文章。
- 文章中应用到的无线控制和多维状态机两个重要的开发应用,会在后面的文章中陆续更新。
使用环境
1.本人使用window10+VMware+ubuntu 18.04 这里不多阐述
2.按照官方文档移植XR806的FreeRTOS
项目介绍
基于XR806——FreeRTOS为项目主控,部署先进模糊控制器,实现对于竞技机器人的机构控制和定位控制等。


软硬件框架

控制部署
继电推理
在封装好电机驱动电流环时,实现对电机的控制,相当于建立了一种
继电特性的非线性控制,此时使用继电整定法的Z-N临界比例度法去建立模糊域。
根据以下临界系数表,整定求出模糊域。
| 控制器类型 | KP | Tn | Tv | Ki | Kd |
|---|---|---|---|---|---|
| P | 0.5*Kμ | — | — | — | — |
| PD | 0.8*Kμ | — | 0.12*Tμ | — | KP*Tn |
| PI | 0.45*Kμ | 0.85*Tμ | — | KP/Tn | — |
| PID | 0.6*Kμ | 0.5*Tμ | 0.12*Tμ | KP/ Tn | KP*Tn |
模糊推理
模糊推理的核心就是计算出E和EC的隶属度。同时把E和EC分为多种子集情况:负最大NB,负中NM,负小NS,零ZO,正小PS,正中PM,正大PB等七种情况。然后计算E/EC种子集的隶属度。
清晰化
进行模糊推理后,可以根据计算的隶属度,建立模糊规则表,实现对输出值的清晰化。对应到应用层的输出函数,实现控制输出。
例图:

FOC控制

仿真效果


代码实现
以下提供部分代码:
自动整定
void PID_AutoTune_Task(void)
{if(pid.AutoRegurating_Status != START) return;/*定义临界Tc*/float Tc = 0.0;static int start_cnt; //记录最大值出现的时间static int end_cnt; //记录周期结束时的时间值 static uint16_t cool_cnt = 0; static uint16_t heat_cnt = 0;// pid.Autotune_Cnt ++; //计数if((pid.Pv_position == UP) && (pid.Pv < pid.Sv)) {cool_cnt ++;if(cool_cnt >= 3) //连续三次都越过,则说明真的越过了{pid.Pv_position = DOWN; //标记当前在下方了pid.Zero_Across_Cnt ++; //标记穿越一次cool_cnt = 0;}}else if((pid.Pv_position == DOWN)&&(pid.Pv > pid.Sv))//刚才在下方,现在在上方{heat_cnt++;if(heat_cnt >= 3) //连续三次都越过,则说明真的越过了{pid.Pv_position = UP; //标记当前在下方了pid.Zero_Across_Cnt ++; //标记穿越一次heat_cnt = 0;} }/*****************开始计算强行振荡的周期****************************/ if((pid.Zero_Across_Cnt == 2)&&(start_cnt == 0)){start_cnt = pid.Autotune_Cnt;printf("start_time = %d\r\n", start_cnt);}else if((pid.Zero_Across_Cnt == 4)&&(end_cnt == 0)){end_cnt = pid.Autotune_Cnt;printf("start_time = %d\r\n", end_cnt);}if(pid.Zero_Across_Cnt == 4){ /*计算一个震荡周期的时间*/if(start_cnt > end_cnt)Tc = (start_cnt-end_cnt)/2; elseTc = (end_cnt-start_cnt)/2; /*计算Kp,Ti和Td*/pid.Kp = 0.6*pid.Kp;pid.Ti = Tc*0.5; pid.Td = Tc*0.12; /*PID参数整定完成,将各项数据清0*/heat_cnt = 0;cool_cnt = 0; pid.Autotune_Cnt = 0;start_cnt = 0;end_cnt = 0; pid.SEk = 0;pid.Zero_Across_Cnt = 0; pid.AutoRegurating_EN = OFF;pid.AutoRegurating_Status = OVER; //开始运行使用新的参数后的PID算法pid.Sv = pid.BKSv; }
}
模糊控制
/*模糊规则表*/
int KpRule[7][7]= { /*NB, NM, NS, ZO, PS, PM, PB -EC*/{1, 1, 1, 1, 1, 1, 1}, //NB 0~-10{0, 0, 0, 1, 2, 3, 4}, //NM 0~10{0, 0, 0, 1, 2, 3, 4}, //NS 10~20 {0, 0, 1, 1, 2, 3, 4}, //20~30{1, 1, 1, 1, 2, 3, 4}, //30~40{1, 1, 1, 1, 2, 3, 4}, //40 ~50{6, 6, 6, 6, 6, 6, 6}, //50~60
};
static float fuzzy_kp(float err, float errchange)
{ volatile float Kp_calcu; volatile uint8_t num,pe,pec; volatile float eFuzzy[2]={0.0,0.0}; //隶属于误差E的隶属程度 volatile float ecFuzzy[2]={0.0,0.0}; //隶属于误差变化率EC的隶属程度 float KpFuzzy[7]={0.0,0.0,0.0,0.0,0.0,0.0,0.0}; //隶属于Kp的隶属程度 /*****误差E隶属函数描述*****/ if(err<eRule[0]) { eFuzzy[0] =1.0; pe = 0; } else if(eRule[0]<=err && err<eRule[1]) { eFuzzy[0] = (eRule[1]-err)/(eRule[1]-eRule[0]); pe = 0; } else if(eRule[1]<=err && err<eRule[2]) { eFuzzy[0] = (eRule[2] -err)/(eRule[2]-eRule[1]); pe = 1; } else if(eRule[2]<=err && err<eRule[3]) { eFuzzy[0] = (eRule[3] -err)/(eRule[3]-eRule[2]); pe = 2; } else if(eRule[3]<=err && err<eRule[4]) { eFuzzy[0] = (eRule[4]-err)/(eRule[4]-eRule[3]); pe = 3; } else if(eRule[4]<=err && err<eRule[5]) { eFuzzy[0] = (eRule[5]-err)/(eRule[5]-eRule[4]); pe = 4; } else if(eRule[5]<=err && err<eRule[6]) { eFuzzy[0] = (eRule[6]-err)/(eRule[6]-eRule[5]); pe = 5; } else { eFuzzy[0] = 0.0; pe = 6; } eFuzzy[1] =1.0 - eFuzzy[0]; /*****误差变化率EC隶属函数描述*****/ if(errchange<ecRule[0]) { ecFuzzy[0] =1.0; pec = 0; } else if(ecRule[0]<=errchange && errchange<ecRule[1]) { ecFuzzy[0] = (ecRule[1] - errchange)/(ecRule[1]-ecRule[0]); pec = 0 ; } else if(ecRule[1]<=errchange && errchange<ecRule[2]) { ecFuzzy[0] = (ecRule[2] - errchange)/(ecRule[2]-ecRule[1]); pec = 1; } else if(ecRule[2]<=errchange && errchange<ecRule[3]) { ecFuzzy[0] = (ecRule[3] - errchange)/(ecRule[3]-ecRule[2]); pec = 2 ; } else if(ecRule[3]<=errchange && errchange<ecRule[4]) { ecFuzzy[0] = (ecRule[4]-errchange)/(ecRule[4]-ecRule[3]); pec=3; } else if(ecRule[4]<=errchange && errchange<ecRule[5]) { ecFuzzy[0] = (ecRule[5]-errchange)/(ecRule[5]-ecRule[4]); pec=4; } else if(ecRule[5]<=errchange && errchange<ecRule[6]) { ecFuzzy[0] = (ecRule[6]-errchange)/(ecRule[6]-ecRule[5]); pec=5; } else { ecFuzzy[0] =0.0; pec = 5; } ecFuzzy[1] = 1.0 - ecFuzzy[0]; /*********查询模糊规则表*********/ num = KpRule[pe][pec]; KpFuzzy[num] += (eFuzzy[0]*ecFuzzy[0]); num = KpRule[pe][pec+1]; KpFuzzy[num] += (eFuzzy[0]*ecFuzzy[1]); num =KpRule[pe+1][pec]; KpFuzzy[num] += (eFuzzy[1]*ecFuzzy[0]); num = KpRule[pe+1][pec+1]; KpFuzzy[num] += (eFuzzy[1]*ecFuzzy[1]); /*********加权平均法解模糊*********/ Kp_calcu = KpFuzzy[0]*kpRule[0] +KpFuzzy[1]*kpRule[1]+ \KpFuzzy[2]*kpRule[2] +KpFuzzy[3]*kpRule[3]+ \KpFuzzy[4]*kpRule[4] +KpFuzzy[5]*kpRule[5]+ \+KpFuzzy[6]*kpRule[6]; printf(" %f,%f,%d,%d,kp = %f\r\n", err, errchange, pe, pec, Kp_calcu);return(Kp_calcu);
}
实物展示
无刷电机控制
https://www.bilibili.com/video/BV1FN4y1C7fY/?aid=874778769&cid=1302701130&page=null
整体定位控制
https://www.bilibili.com/video/BV1NN411t7Fy/?aid=492262076&cid=1302702003&page=null
以上,就是本文分享的全部内容了,感谢各位