优化问题，详解静态优化

优化问题，尤其静态优化问题，在控制系统设计中随处可见，例如基于燃油经济性和驾驶体验的多目标优化的汽车发动机 MAP 标定，基于性能指标优化的飞行器结构设计参数优化，以实验数据与模型输出匹配为目标的电池 RC 等效电路模型标定等等，他们都是通过构建目标函数（某个值的性能最大，或者某两个值之间的差距最小），然后调用优化算法实现设计变量寻优。

当设计变量变成一个函数，而这个函数对系统指标的影响又在时间先后上取决于一个动力学约束，这时候我们可能依然可以通过离散的方式将问题变成静态优化问题，当然这类问题也可以通过最优控制理论来实现，利用庞特里亚金极小值原理，动态规划来求解。例如混动车辆的 ECMS 算法，输出电池和发动机的能量分配序列满足电池 SOC 平衡的基础上油耗最低。

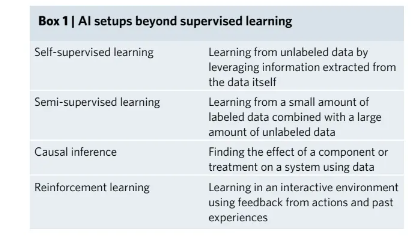
随着 AI 的引入，即使我们对于系统或模型一无所知，我们又可以通过试错的方式来获得一个长期奖励较优的控制器，用于处理序列决策问题，例如自动驾驶车辆或智能机器人的控制器控制序列，也就是强化学习的思路。本文接下来通过MATLAB示例来简单介绍这些概念的思想。

优化问题

对于一个普通的静态优化问题，可以描述为求解最优变量 x 使得 f(x) 最小[1]，

同时满足约束条件：

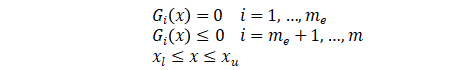
其中 x 是 n 维的设计变量向量，f(x) 是目标函数（通常是标量），和 m 维的函数向量 G(x),用于计算 x 处的等式和非等式约束。例如，求解这个示例：

目标函数

约束

这个示例是典型的包含非线性约束的平滑问题，为了迭代高效，可以在目标函数和约束函数计算时中同时给出梯度。

function [f,gf] = onehump(x)

% ONEHUMP Helper function for Tutorial for the Optimization Toolbox demo

% Copyright 2008-2009 The MathWorks, Inc.

r = x(1)^2 + x(2)^2;

s = exp(-r);

f = x(1)*s+r/20;

gf = [(1-2*x(1)^2)*s+x(1)/10;

-2*x(1)*x(2)*s+x(2)/10];

end

function [c,ceq,gc,gceq] = tiltellipse(x)

% TILTELLIPSE Helper function for Tutorial for the Optimization Toolbox demo

% Copyright 2008-2009 The MathWorks, Inc.

c = x(1)*x(2)/2 + (x(1)+2)^2 + (x(2)-2)^2/2 - 2;

ceq = [];

gc = [x(2)/2+2*(x(1)+2);

x(1)/2+x(2)-2];

gceq = [];

end

构建完目标函数和约束函数，这样就可以调用 fmincon 求解器求解这个非线性平滑约束的优化问题，

options = optimoptions(options,...

'SpecifyObjectiveGradient',true,...

'SpecifyConstraintGradient',true);

[x,fval,exitflag,output] = fmincon(@onehump,x0,[],[],[],[],[],[], ...

@tiltellipse,options);

xold = x

xold = 2x1

- 0.9727

0.4686

于是得到约束条件下的最优解（红色的点）:

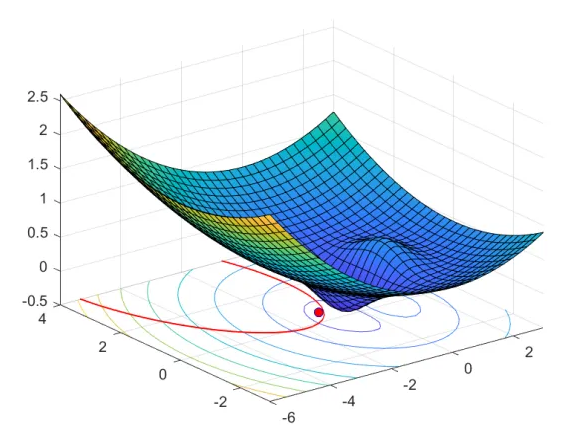
这类有约束的问题中，我们的优化变量是数值向量，我们可以通过 MATLAB 内置的求解器来求解极值点（算法参考[2]），也可以使用符号数学工具箱，利用函数的极值条件，手动构建 Lagrange multiplier（将等式约束问题转换为无约束问题）或者KKT条件进行求解，例如，针对 Lagrange multiplier 方法，在 g(x)=0 的等式约束条件下求解 f(x) 最小，可以先构造 Lagrangian 函数：

需要满足极值条件：

我们可以用这种方法求解优化问题（1-1）（因为有不等式约束，下面的脚本添加了 s1 项变成等式约束，读者也可以尝试使用 KKT 条件进行含不等式约束问题的求解），可以得到和数值求解相同的结果。

syms x y s1 lambda

f = x.*exp(-x.^2-y.^2)+(x.^2+y.^2)/20;

g = x.*y/2+(x+2).^2+(y-2).^2/2-2+s1^2==0;

L = f + lambda*lhs(g);

dL_dx = diff(L,x)==0;

dL_dy = diff(L,y)==0;

% derivative of L with respect to lambda

dL_dlambda = diff(L,lambda) == 0;

dL_ds1=diff(L,s1) == 0;

% build the system of equations

system = [dL_dx; dL_dy; dL_dlambda;dL_ds1];

% solve the system of equations

[x_val, y_val, lambda_val, s1_val] = ...

solve(system, [x y lambda s1], 'Real', true);

% show results in a vector of data type double

results_numeric = double([x_val; y_val])

results_numeric = 2x1

- 0.9727

0.4686

免费分享一些我整理的人工智能学习资料给大家，整理了很久，非常全面。包括一些人工智能基础入门视频+AI常用框架实战视频、图像识别、OpenCV、NLP、YOLO、机器学习、pytorch、计算机视觉、深度学习与神经网络等视频、课件源码、国内外知名精华资源、AI热门论文等。

下面是部分截图，加我免费领取