代码随想录第二十三天（一刷C语言）|组合总数组合总数II分割回文串

创作目的：为了方便自己后续复习重点，以及养成写博客的习惯。

一、组合总数

思路：参考carl文档

定义两个全局变量，二维数组result存放结果集，数组path存放符合条件的结果。（这两个变量可以作为函数参数传入）。题目中给出的参数，集合是candidates, 和目标值是target。终止只有两种情况，sum大于target和sum等于target。

ledcode题目：https://leetcode.cn/problems/combination-sum/

AC代码：

int* path;
int pathTop;
int** ans;
int ansTop;
//记录每一个和等于target的path数组长度
int* length;void backTracking(int target, int index, int* candidates, int candidatesSize, int sum) {//若sum>=target就应该终止遍历if(sum >= target) {//若sum等于target，将当前的组合放入ans数组中if(sum == target) {int* tempPath = (int*)malloc(sizeof(int) * pathTop);int j;for(j = 0; j < pathTop; j++) {tempPath[j] = path[j];}ans[ansTop] = tempPath;length[ansTop++] = pathTop;}return ;}int i;for(i = index; i < candidatesSize; i++) {//将当前数字大小加入sumsum+=candidates[i];path[pathTop++] = candidates[i];backTracking(target, i, candidates, candidatesSize, sum);sum-=candidates[i];pathTop--;}
}int** combinationSum(int* candidates, int candidatesSize, int target, int* returnSize, int** returnColumnSizes){//初始化变量path = (int*)malloc(sizeof(int) * 50);ans = (int**)malloc(sizeof(int*) * 200);length = (int*)malloc(sizeof(int) * 200);ansTop = pathTop = 0;backTracking(target, 0, candidates, candidatesSize, 0);//设置返回的数组大小*returnSize = ansTop;*returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);int i;for(i = 0; i < ansTop; i++) {(*returnColumnSizes)[i] = length[i];}return ans;
}

二、组合总和II

思路：参考carl文档

与组合总数的区别在于组合总和II中的candidates 每个数字在每个组合中只能使用一次，需要使用降重处理。

lecode题目：https://leetcode.cn/problems/combination-sum-ii/description/

AC代码：

int* path;
int pathTop;
int** ans;
int ansTop;
//记录ans中每一个一维数组的大小
int* length;
int cmp(const void* a1, const void* a2) {return *((int*)a1) - *((int*)a2);
}void backTracking(int* candidates, int candidatesSize,  int target, int sum, int startIndex) {if(sum >= target) {//若sum等于target，复制当前path进入if(sum == target) {int* tempPath = (int*)malloc(sizeof(int) * pathTop);int j;for(j = 0; j < pathTop; j++) {tempPath[j] = path[j];}length[ansTop] = pathTop;ans[ansTop++] = tempPath;}return ;}int i;for(i = startIndex; i < candidatesSize; i++) {//对同一层树中使用过的元素跳过if(i > startIndex && candidates[i] == candidates[i-1])continue;path[pathTop++] = candidates[i];sum += candidates[i];backTracking(candidates, candidatesSize, target, sum, i + 1);//回溯sum -= candidates[i];pathTop--;}
}int** combinationSum2(int* candidates, int candidatesSize, int target, int* returnSize, int** returnColumnSizes){path = (int*)malloc(sizeof(int) * 50);ans = (int**)malloc(sizeof(int*) * 100);length = (int*)malloc(sizeof(int) * 100);pathTop = ansTop = 0;//快速排序candidates，让相同元素挨到一起qsort(candidates, candidatesSize, sizeof(int), cmp);backTracking(candidates, candidatesSize, target, 0, 0);*returnSize = ansTop;*returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);int i;for(i = 0; i < ansTop; i++) {(*returnColumnSizes)[i] = length[i];}return ans;
}

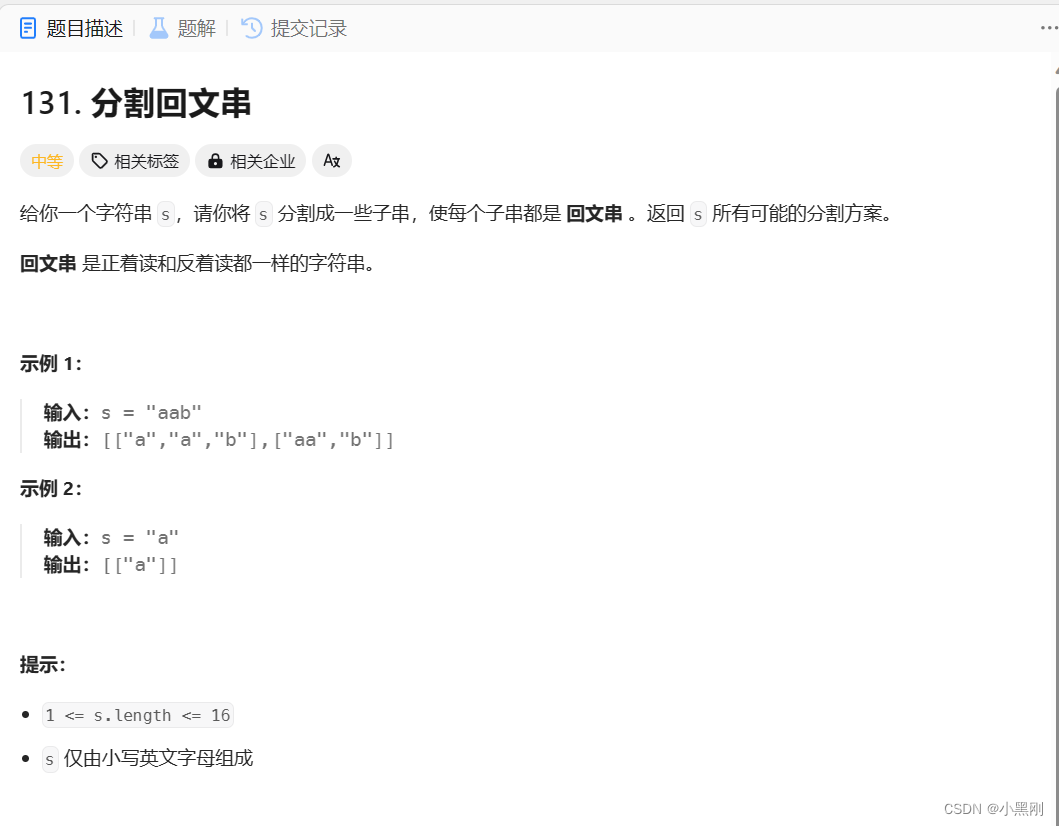
三、分割回文串

思路：参考carl文档

考虑切割并判断回文，递归用来纵向遍历，for循环用来横向遍历。切割问题的回溯搜索的过程和组合问题的回溯搜索类似。组合问题与切割问题的区别：

1、组合问题：选取一个a之后，在bcdef中再去选取第二个，选取b之后在cdef中再选取第三个.....。

2、切割问题：切割一个a之后，在bcdef中再去切割第二段，切割b之后在cdef中再切割第三段.....。

全局变量数组path存放切割后回文的子串，二维数组result存放结果集。递归函数参数还需要startIndex，切割过的地方，不能重复切割，和组合问题一样。递归参数需要传入startIndex，表示下一轮递归遍历的起始位置，而startIndex就是切割线。

ledcode题目：https://leetcode.cn/problems/palindrome-partitioning/description/

AC代码：

char** path;
int pathTop;
char*** ans;
int ansTop = 0;
int* ansSize;//将path中的字符串全部复制到ans中
void copy() {//创建一个临时tempPath保存path中的字符串char** tempPath = (char**)malloc(sizeof(char*) * pathTop);int i;for(i = 0; i < pathTop; i++) {tempPath[i] = path[i];}//保存tempPathans[ansTop] = tempPath;//将当前path的长度（pathTop）保存在ansSize中ansSize[ansTop++] = pathTop;
}//判断字符串是否为回文字符串
bool isPalindrome(char* str, int startIndex, int endIndex) {//双指针法：当endIndex（右指针）的值比startIndex（左指针）大时进行遍历while(endIndex >= startIndex) {//若左指针和右指针指向元素不一样，返回Falseif(str[endIndex--] != str[startIndex++])return 0;}return 1;
}//切割从startIndex到endIndex子字符串
char* cutString(char* str, int startIndex, int endIndex) {//开辟字符串的空间char* tempString = (char*)malloc(sizeof(char) * (endIndex - startIndex + 2));int i;int index = 0;//复制子字符串for(i = startIndex; i <= endIndex; i++)tempString[index++] = str[i];//用'\0'作为字符串结尾tempString[index] = '\0';return tempString;
}void backTracking(char* str, int strLen,  int startIndex) {if(startIndex >= strLen) {//将path拷贝到ans中copy();return ;}int i;for(i = startIndex; i < strLen; i++) {//若从subString到i的子串是回文字符串，将其放入path中if(isPalindrome(str, startIndex, i)) {path[pathTop++] = cutString(str, startIndex, i);}//若从startIndex到i的子串不为回文字符串，跳过这一层 else {continue;}//递归判断下一层backTracking(str, strLen, i + 1);//回溯，将path中最后一位元素弹出pathTop--;}
}char*** partition(char* s, int* returnSize, int** returnColumnSizes){int strLen = strlen(s);//因为path中的字符串最多为strLen个（即单个字符的回文字符串），所以开辟strLen个char*空间path = (char**)malloc(sizeof(char*) * strLen);//存放path中的数组结果ans = (char***)malloc(sizeof(char**) * 40000);//存放ans数组中每一个char**数组的长度ansSize = (int*)malloc(sizeof(int) * 40000);ansTop = pathTop = 0;//回溯函数backTracking(s, strLen, 0);//将ansTop设置为ans数组的长度*returnSize = ansTop;//设置ans数组中每一个数组的长度*returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);int i;for(i = 0; i < ansTop; ++i) {(*returnColumnSizes)[i] = ansSize[i];}return ans;
}