给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
示例 1:
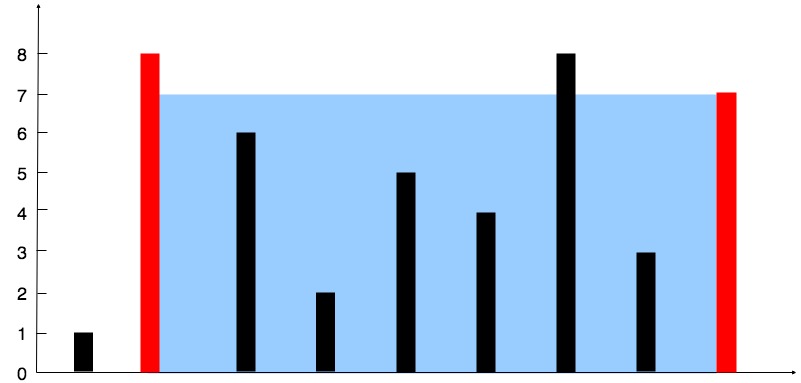
输入:[1,8,6,2,5,4,8,3,7] 输出:49 解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:
输入:height = [1,1] 输出:1
提示:
n == height.length2 <= n <= 1050 <= height[i] <= 104
题解
看到这个题第一个想法是两层循环找最大的乘积
class Solution {
public:int maxArea(vector<int>& height) {auto capacity=[&height](int begin,int end)->int{int h=height[begin]<height[end]?height[begin]:height[end];int width=end-begin;return h*width;};int max=0;for(int i=0;i<height.size()-1;i++){for(int j=i+1;j<height.size();j++){int c=capacity(i,j);max=max<c?c:max;}}return max;}
};但是超时了
我们把两层循环改成一层循环,使用双指针的方法,让left=0,right=n-1,从两侧的木板开始计算容量
计算完这两块木板的容量之后,我们需要换掉一块木板继续计算容量,换掉哪一块木板呢,我们应该换掉短的那一块木板,因为如果换掉长的那一块木板,那么我们的容量只能缩小,因为容器的高度已经由最短的那块木板决定了,由于我们是从外侧开始换木板的,因此容器的宽度只能缩短不能变长
所以我们每次换掉最短的那一块木板,然后在过程中更新最大容量
class Solution {
public:int maxArea(vector<int>& height) {auto capacity=[&height](int begin,int end)->int{int h=height[begin]<height[end]?height[begin]:height[end];int width=end-begin;return h*width;};int max=0;int left=0,right=height.size()-1;while(left!=right){int c=capacity(left,right);max=max<c?c:max;if(height[left]<height[right]){left++;}else{right--;}}return max;}
};