文章目录
- 专题一:栈系列
- 1. 中缀表达式转后缀表达式(逆波兰式)
- 2. 有效的括号
- 3. 用栈实现队列
- 4. 最小栈
专题一:栈系列
1. 中缀表达式转后缀表达式(逆波兰式)

算法原理

2. 有效的括号
题目链接
算法原理
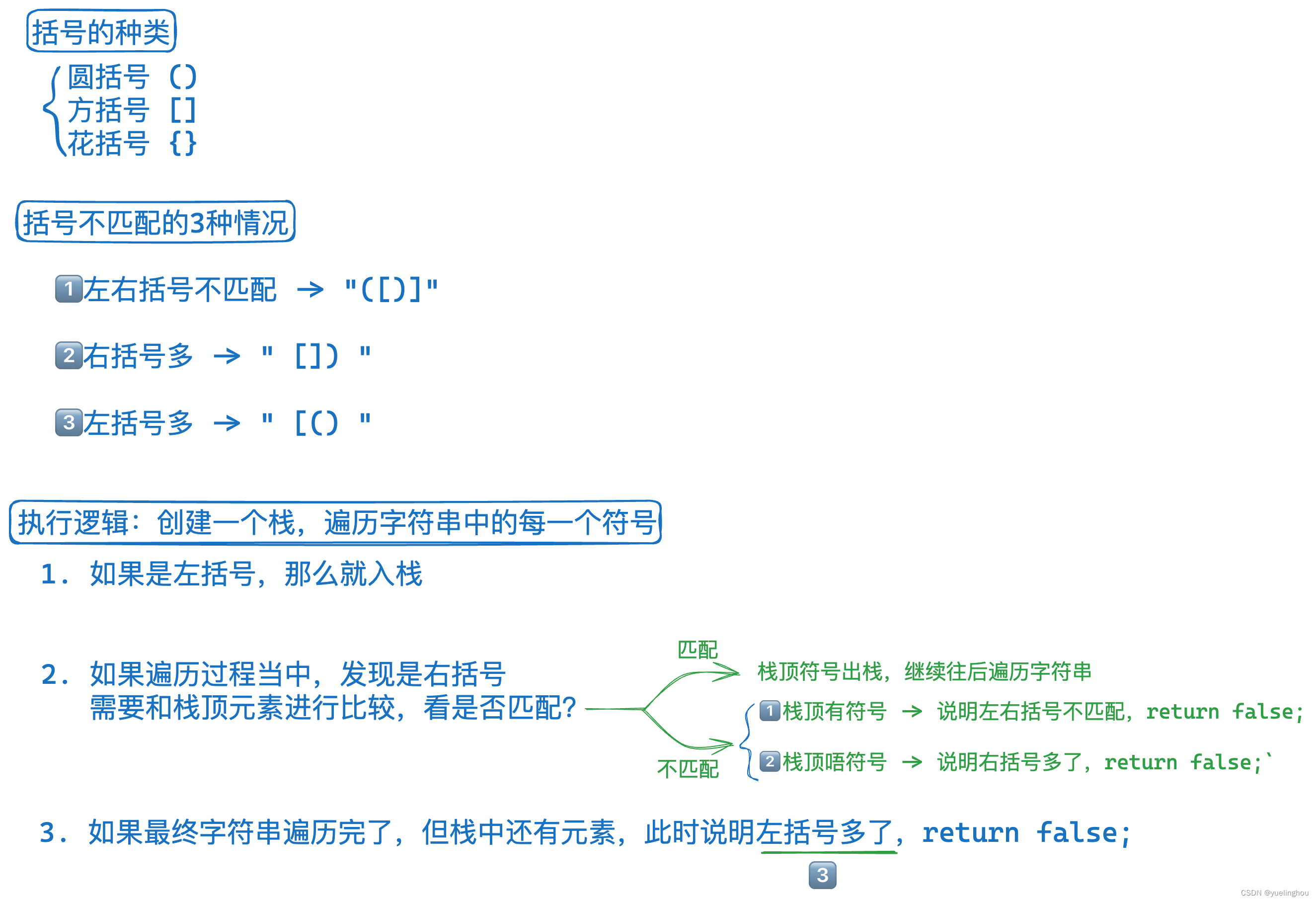
代码编写
class Solution
{
public:bool isValid(string s) {stack<char> st;for(const auto ch : s){if(ch == '(' || ch == '[' || ch == '{') st.push(ch);else {// 1、右括号多if(st.empty()) return false;char top = st.top();if(top == '(' && ch == ')' || top == '[' && ch == ']' || top == '{' && ch == '}') st.pop();else return false; // 2、括号不匹配}}return st.empty(); // 3、最后若栈为空,说明左括号全部正确匹配完成}
};
3. 用栈实现队列
题目链接
算法原理
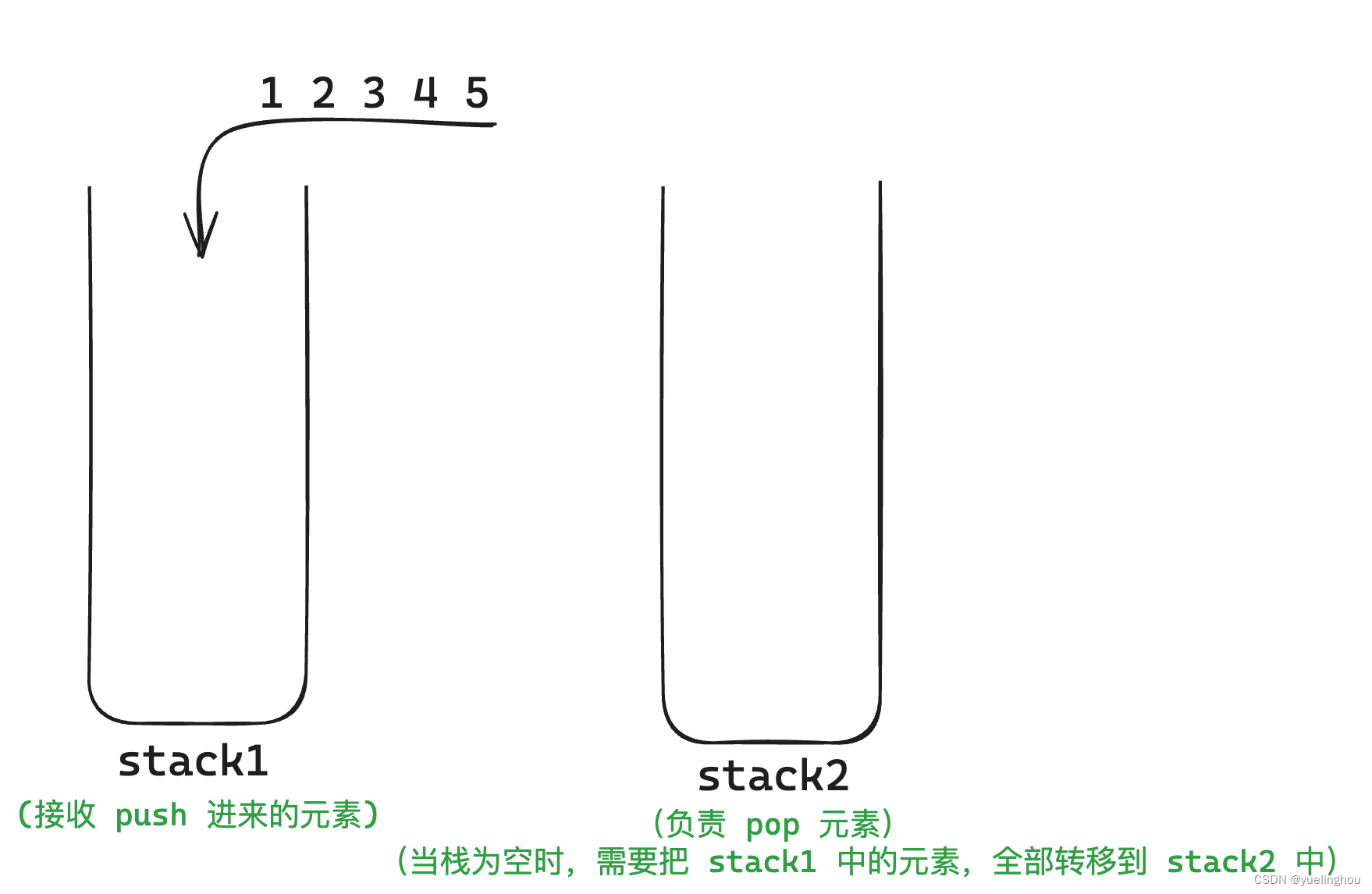
代码编写
class MyQueue
{
private:stack<int> st1; //负责入队列stack<int> st2; //负责出队列public:// 构造函数,什么都不需要做MyQueue() {}// 入队列void push(int x) {st1.push(x);}// 出队列int pop() {// 队列为空,则返回-1if(st1.empty() && st2.empty()) return -1; // 若 st2 为空,则需要从 st1 中把元素更新过来if(st2.empty()) {while(!st1.empty()) {st2.push(st1.top());st1.pop();}}// st2 栈顶元素即使队列的对首元素,删除即可int ans = st2.top();st2.pop();return ans;}int peek() {// 队列为空,则返回-1if(st1.empty() && st2.empty()) return -1;// 若 st2 为空,则需要从 st1 中把元素更新过来if(st2.empty()){while(!st1.empty()) {st2.push(st1.top());st1.pop();}}// st2 栈顶元素即使队列的对首元素,返回即可return st2.top();}// 队列判空bool empty() {return st1.empty() && st2.empty();}
};
4. 最小栈
题目链接
算法原理
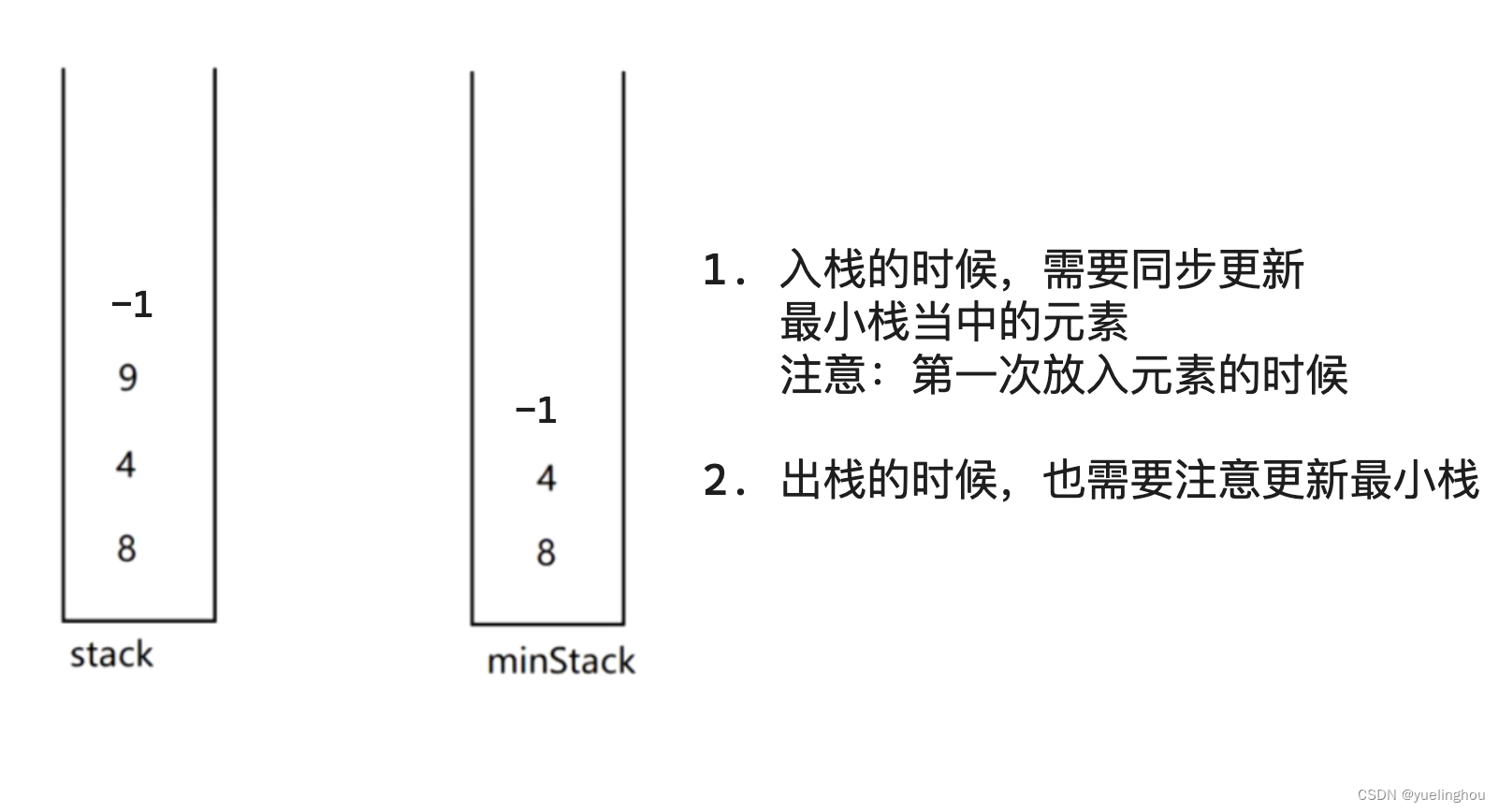
代码编写
class MinStack
{
private:stack<int> st; //存放栈元素stack<int> minSt;//存放st中,最小元素序列public:// 默认构造函数MinStack() {}// 栈中插入元素void push(int val) {st.push(val);// 1、若最小栈为空(说明是第一个插入元素),此时 val 直接入最小栈// 2、若最小栈不为空,则比较最小栈栈顶元素,再决定是否插入最小栈if(minSt.empty()) minSt.push(val);else{if(val <= minSt.top()) minSt.push(val);}}// 弹出栈顶元素void pop() {// 若栈顶元素为栈中最小元素,则需要同步更新最小栈if(st.top() == minSt.top()) minSt.pop();// 弹出栈顶元素st.pop();}// 获取栈顶元素int top() {return st.top();}// 获取栈中最小元素int getMin() {return minSt.top();}
};

![Java生成word[doc格式转docx]](https://img-blog.csdnimg.cn/direct/7c522fa012d146a792758b3ea2cc0525.png)