基于集成学习的共享单车异常检测的研究
整体求解过程概述(摘要)
近年来,共享单车的快速发展在方便了人们出行的同时,也对城市交通产生了一定的负面影响,其主要原因为单车资源配置的不合理。本文通过建立单车租赁数量的预测模型和异常检测模型,以期能够帮助城市合理配置资源。
首先,进行探索性数据分析。主要步骤为数据预处理、描述性统计和回归分析。其中,分位数回归能够表现出输入变量与输出变量各分位点间的线性关系。
其次,建立单车预测模型。分别运用集成学习中的 Bagging、Boosting 和模型融合算法 Stacking 进行建模。实验结果显示,Boosting 算法中的 CatBoost 模型对单车租赁数量的预测效果最好。
最后,建立异常检测模型。运用孤立森林算法检测单车租赁数量的异常值,并利用支持向量机分析各输入变量对租赁异常的影响程度。研究表明,租赁异常可能与城市意外事件的发生、节假日的到来、温度与风速以及湿度的突变和极端恶劣天气的产生有关。预测模型能够帮助城市合理规划共享单车的投放数量,而异常检测模型则有助于城市及时处理突发事件,希望本文的研究能够为城市资源合理配置提供参考。
问题分析
首先,本文对该共享单车数据集进行了探索性数据分析。探索性数据分析用于解释原始数据,并挖掘数据的潜在规律。第一步,进行数据预处理,即对数值特征的归一化处理和对类别特征的哑变量处理。该预处理方法有利于数据建模分析。第二步,进行描述性统计,本文绘制了小提琴图和饼状图,借以表现各特征变量的概率分布情况。第三步,进行回归分析,其中,相比于线性回归,分位数回归能够表现出解释变量与被解释变量各分位点之间的线性关系,其解释数据效果更好。
其次,本文对该数据集进行了集成学习研究。集成学习是指将若干个弱学习器通过一定的策略组合得到一个强学习器,其基本分类为 Bagging、Boosting 和Stacking。第一步,运用随机森林、XGBoost、LightBoost 和 CatBoost 四种模型分别对该数据集进行训练,并探究其特征变量重要性。随机森林是集成决策树的Bagging 算法,其学习结果由其决策树的投票产生。XGBoost、LightGBM 和CatBoost 均属于 Boosting 算法,其中,XGBoost 对损失函数进行改进,并利用正则化减少过拟合,提高了模型的泛化能力。LightGBM 支持并行化学习,在处理多维问题时其计算效率更高;CatBoost 在处理类别特征问题上进行了优化,其模型精度往往比 XGBoost 和 LightGBM 更高。第二步,运用 Stacking 方法将上述四种算法进行模型融合,以期得到一个泛化能力更好的模型。Stacking 是模型融合的学习框架,其核心思想是将不同模型的优点进行有机结合,从而提高模型的泛化能力。
最后,本文以上述模型的训练误差为样本对单车租赁数量进行异常检测研究。第一步,运用孤立森林模型检测样本中的异常点,以期通过误差异常来反映共享单车租赁数量异常。孤立森林是一种异常检测方法,可以精准识别分布稀疏的独立离群点。第二步,运用支持向量机对上述异常情况进行训练,支持向量机非常擅长分类及回归问题,以期通过其向量空间特征系数来反映各变量对单车租赁数量异常的影响程度。集成学习所建立的预测模型能够帮助城市合理规划共享单车的投放数量,而孤立森林和支持向量机所建立的异常检测模型则有助于城市及时处理突发事件。本文研究方法的流程图如下图 1 所示:
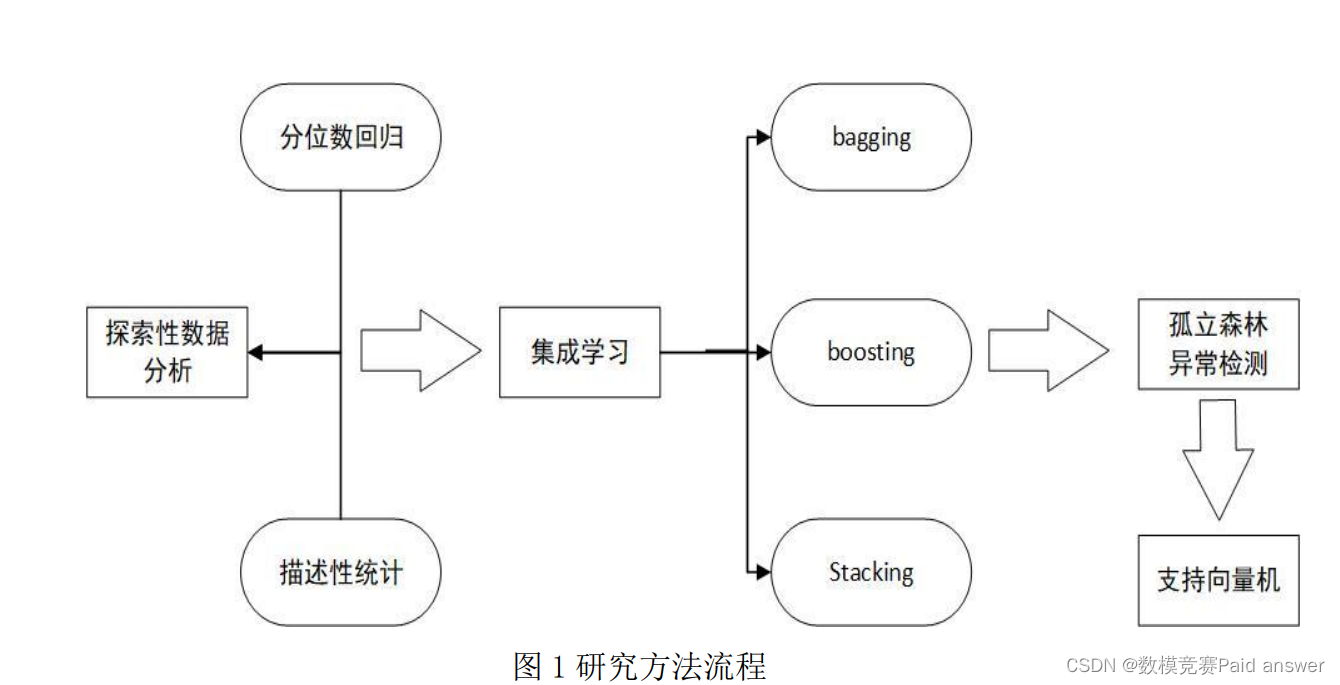
其中,探索性数据分用于解释数据,集成学习用于构造预测模型,孤立森林和支持向量机用于构造检测模型。
模型的建立与求解(部分)
对于该数据集中的数值型变量,即数值特征,本文对其进行数据归一化,即统一映射到[0, 1]区间上;数据无量纲化有利于提升机器学习模型的训练精度和收敛速度,其公式如下:
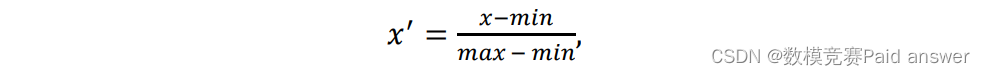
其中,𝑥代表原始数据,𝑥′代表归一化后的数据,𝑚𝑎𝑥代表原始数据中最大值,𝑚𝑖𝑛代表原始数据中最小值。数值型变量的代表符号如下表 1 所示:

对于该数据集中的分类型变量,即类别特征,本文采用哑变量的处理方式,将其统一变换为 0 或 1 变量。分类型变量的代表符号如下表 2 所示:

本文探索性数据分析和集成学习所用数据均为上述预处理数据。
描述性统计
探索性数据分析(Exploratory Data Analysis,EDA)用于解释原始数据,探索数据之间的潜在规律。EDA 在数据科学工作过程中,能够对多个环节产生影响,是不可或缺的重要步骤。本文采用描述性统计和分位数回归两种方法进行EDA。
小提琴图是箱线图与密度图的结合,可以同时反映出变量的概率密度及分布情况,其中,箱线图的信息在中间部分,密度图的信息在两侧部分。本文主要运用小提琴图对数值型变量进行了 EDA,其结果如下图 2 所示:
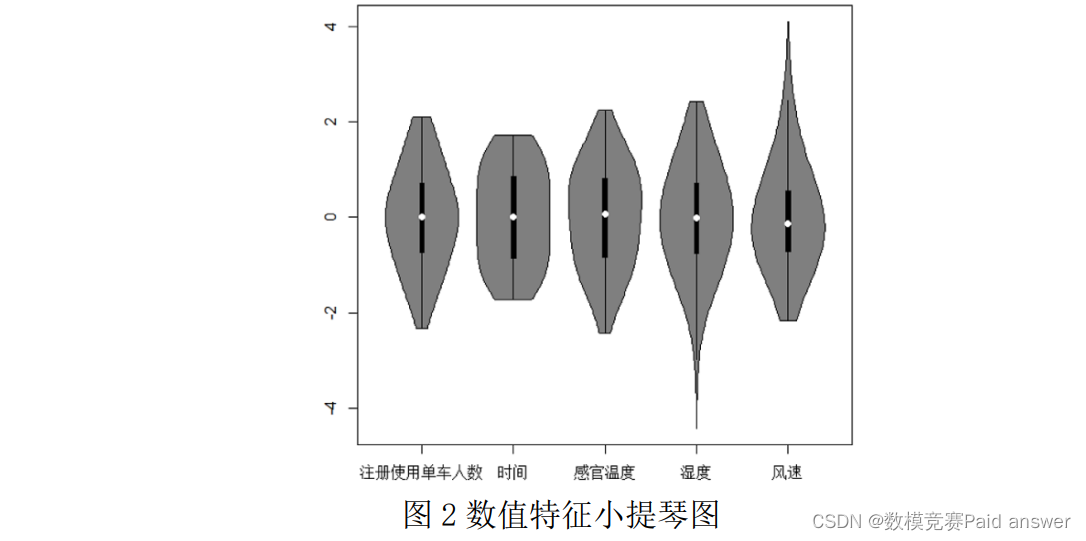
从图 2 中可以看出,单车租赁数量与时间和温度这两个变量主要集中分布在中间区域,各数据间的取值无明显差异;而湿度与风速这两个变量存在极值点,可初步判断这两个变量与单车租赁数量有较大相关性。
对于该数据集中的分类型变量,本文主要运用饼状图进行 EDA,其结果如下图 3 所示:
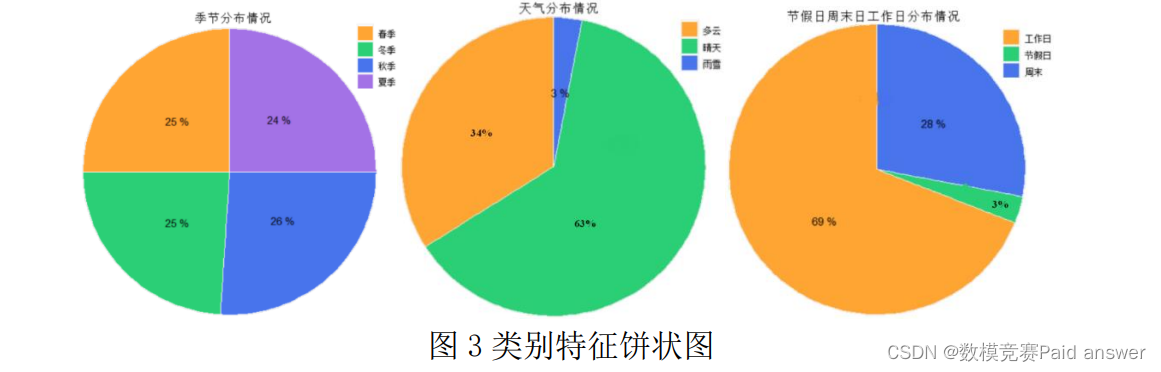
从季节变量饼状图中可以看出,春夏秋冬四季约各为总体的四分之一,说明该数据集的季节变量分布较为均匀;从天气变量饼状图中可以看出,晴天出现的次数最多,约为总体的 63%,而雨雪等极端天气出现的次数最少,仅为 3%;除此之外,工作日所占比重最大,约为总体的 69%,而节假日所占比重最少,仅 3%。

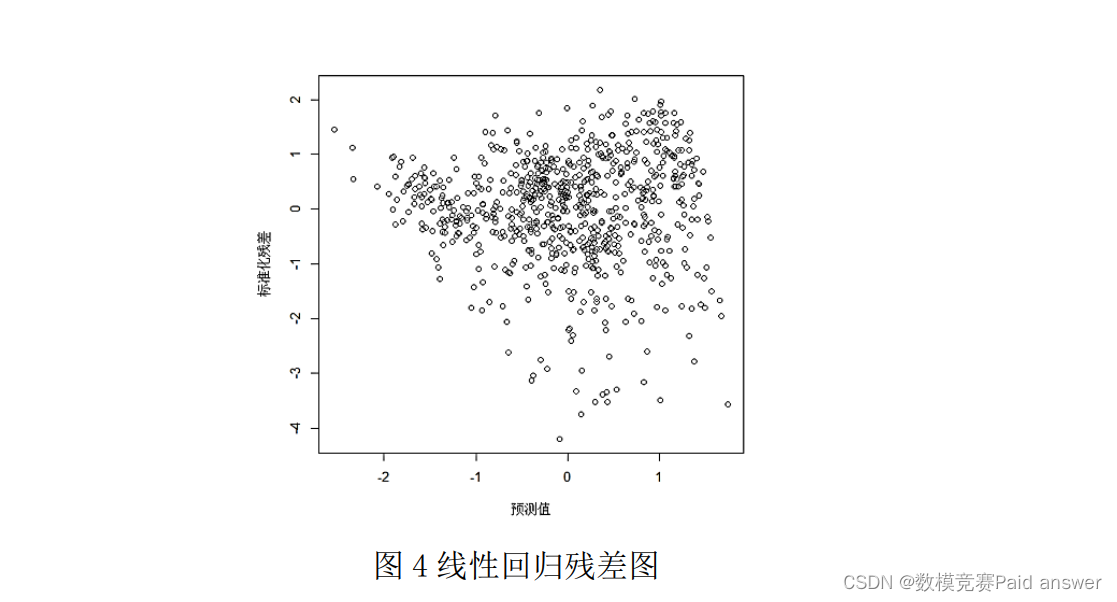
为了方便进行回归分析,本文对季节和天气两个类别特征进行编码化处理,其他数据仍为预处理数据,并进行了线性回归分析,其结果如下图 4 所示:
模型的建立与求解整体论文缩略图


全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
(代码和文档not free)
X - input data, t - number of trees, ψ - subsampling size
输出:a set of t iTrees
1:Initialize Forest
2:set height limit l = ceiling(log2ψ)
3:for i = 1 to t do
4: X’← sample(X, ψ)
5: Forest← Forest∪iTree(X’, 0, l)
6:end for
7:return Forest
输入:X’ – input data
输出:an iTree
1: if X’ cannot be divided then
2: return exNode{Size← | X’ |}
3: else
4: let Q be a list of attribute in X’
5: randomly select an attribute q∈Q
6: randomly select a split point p between the max and min values of attribute q in X’
7: Xl← filter(X’, q < p)
8: Xr← filter(X’, q ≥ p)
9: return inNode{Left← iTree(Xl),
10: Right← iTree(Xr),
11: SplitAtt← q,
12: SplitValue← p}
13: end if
输入:x – an instance, T – an iTree, hlim – height limit, e – current path length;
To be initialized to zero when first called
输出:path length of x
1: if T is an external node or e ≥ hlim then
2: return e + c(T, size) {c(.) is defined in Equation 1}
3: end if
4: α← T.splitAtt
5: if xα < T.splitValue then
6: return PathLength(x, T.Left, hlim, e +1)
7: else {xα ≥ T.splitValue}
8: return PathLength(x, T.Right, hlim, e +1)
9: end if