LeetCode 每日一题 Day 5【Hard】

2646. 最小化旅行的价格总和

现有一棵无向、无根的树，树中有 n 个节点，按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [a_i, b_i] 表示树中节点 a_i 和 b~i ~之间存在一条边。

每个节点都关联一个价格。给你一个整数数组 price ，其中 price[i] 是第 i 个节点的价格。

给定路径的价格总和是该路径上所有节点的价格之和。

另给你一个二维整数数组 trips ，其中 trips[i] = [start_i, end_i] 表示您从节点 start~i ~开始第 i 次旅行，并通过任何你喜欢的路径前往节点 endi 。

在执行第一次旅行之前，你可以选择一些非相邻节点并将价格减半。

返回执行所有旅行的最小价格总和。

示例 1：

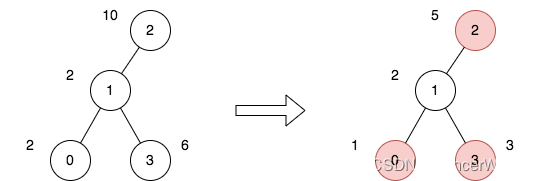
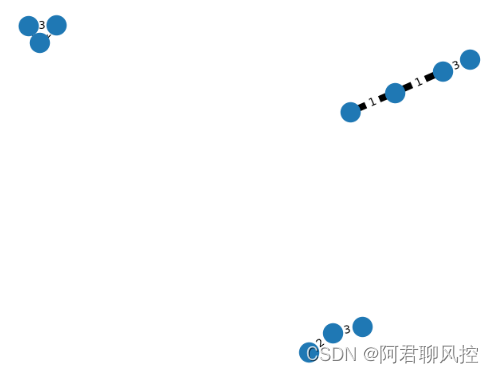
输入：n = 4, edges = [[0,1],[1,2],[1,3]], price = [2,2,10,6], trips = [[0,3],[2,1],[2,3]]
输出：23
解释：
上图表示将节点 2 视为根之后的树结构。第一个图表示初始树，第二个图表示选择节点 0 、2 和 3 并使其价格减半后的树。
第 1 次旅行，选择路径 [0,1,3] 。路径的价格总和为 1 + 2 + 3 = 6 。
第 2 次旅行，选择路径 [2,1] 。路径的价格总和为 2 + 5 = 7 。
第 3 次旅行，选择路径 [2,1,3] 。路径的价格总和为 5 + 2 + 3 = 10 。
所有旅行的价格总和为 6 + 7 + 10 = 23 。可以证明，23 是可以实现的最小答案。
示例 2：

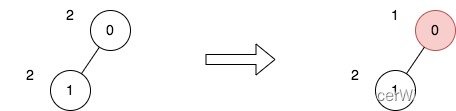
输入：n = 2, edges = [[0,1]], price = [2,2], trips = [[0,0]]
输出：1
解释：
上图表示将节点 0 视为根之后的树结构。第一个图表示初始树，第二个图表示选择节点 0 并使其价格减半后的树。
第 1 次旅行，选择路径 [0] 。路径的价格总和为 1 。
所有旅行的价格总和为 1 。可以证明，1 是可以实现的最小答案。

提示：
1 <= n <= 50
edges.length == n - 1
0 <= a_i, b_i <= n - 1
edges 表示一棵有效的树
price.length == n
price[i] 是一个偶数
1 <= price[i] <= 1000
1 <= trips.length <= 100
0 <= start_i, end_i <= n - 1

这题想了半小时还是没能通过所有数据，开始确实想到使用DFS直接暴力求解，还是太菜了
这里直接把灵神的题解搬了过来：

class Solution {
public:int minimumTotalPrice(int n, vector<vector<int>>& edges, vector<int>& price, vector<vector<int>>& trips) {// 构建树unordered_map<int, vector<int>> graph;for (auto& edge : edges) {int x = edge[0], y = edge[1];graph[x].push_back(y);graph[y].push_back(x);}// 计算每个节点在旅行路径中的出现次数vector<int> occurrences(n);for (auto& trip : trips) {int end = trip[1];function<bool(int, int)> dfs = [&](int current, int parent) -> bool {if (current == end) {occurrences[current]++;return true; // 找到终点}for (int neighbor : graph[current]) {if (neighbor != parent && dfs(neighbor, current)) {occurrences[current]++; // current 是 end 的祖先节点，也就在路径上return true;}}return false; // 未找到终点};dfs(trip[0], -1);}// 递归计算最小总价值function<pair<int, int>(int, int)> dfs = [&](int current, int parent) -> pair<int, int> {int notHalve = price[current] * occurrences[current]; // 当前节点不变int halve = notHalve / 2; // 当前节点减半for (int neighbor : graph[current]) {if (neighbor != parent) {auto [notHalveNeighbor, halveNeighbor] = dfs(neighbor, current);notHalve += min(notHalveNeighbor, halveNeighbor); // 当前节点不变，邻居可以不变或减半，取最小值halve += notHalveNeighbor; // 当前节点减半，邻居只能不变}}return {notHalve, halve};};auto [notHalveResult, halveResult] = dfs(0, -1);return min(notHalveResult, halveResult);}
};