目录
背景
环境
搭建kvm环境
安装ubuntu虚机
虚机设置
系统安装
登录虚机
安装cloud-init
安装cloud-utils-growpart
关闭实例
删除细节信息
删除网卡细节
使虚机脱离libvirt纳管
结束与验证
压缩与转移
验证是否能够正常运行
背景
一般的镜像文件在上传OpenStack之后也无法正常进行安装,适用于OpenStack的镜像可以通过官网进行下载,部分系统官方提供云镜像的下载,也可以通过自己根据需要虚拟化安装之后打包,这里介绍的是centos7环境下通过kvm对Ubuntu18.04版本镜像进行打包的操作。
之所以使用图形化是因为还有很多不熟悉virsh工具的兄弟,也不会使用vnc访问kvm虚机,直接使用virt-manager更为直观也更容易理解
环境
VMwareworkstation17pro
——打开VT
CentOS Linux release 7.9.2009 (Ubuntu也可以,centos8和9都可以,大差不差)
——网络NAT
——50G硬盘,自动分区
镜像版本Ubuntu18.04
bionic-mini.iso
搭建kvm环境
#升级软件包
yum update
#安装kvm的环境
yum -y install qemu-kvm qemu-kvm-tools virt-install qemu-img bridge-utils libvirt virt-manager#用centos9做到一半发现centos9不支持18.04版本的安装了,很尴尬
#获取镜像,例子中使用的是一个64M的小型镜像,也可以自己下载好传到虚拟机里
wget -O /var/lib/libvirt/boot/bionic-mini.iso \http://archive.ubuntu.com/ubuntu/dists/bionic/main/installer-amd64/current/images/netboot/mini.iso#创建一个10G的卷文件
qemu-img create -f qcow2 /var/lib/libvirt/images/bionic.qcow2 10G#打开virt-manager
virt-manager安装ubuntu虚机
虚机设置
找到并选择刚刚下载的镜像
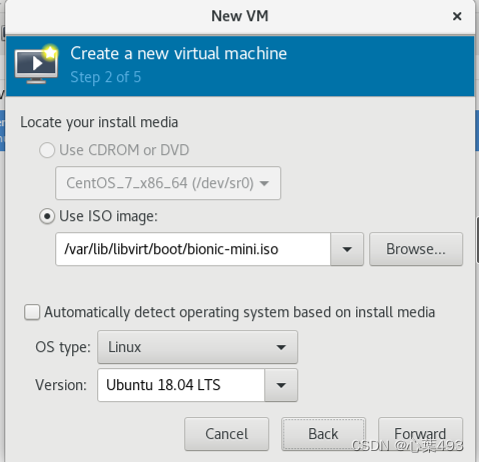
选择内存和vCPU个数,其实这个不太有所谓
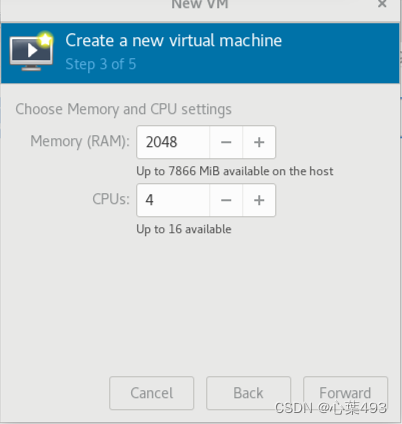
选择刚刚创建的卷
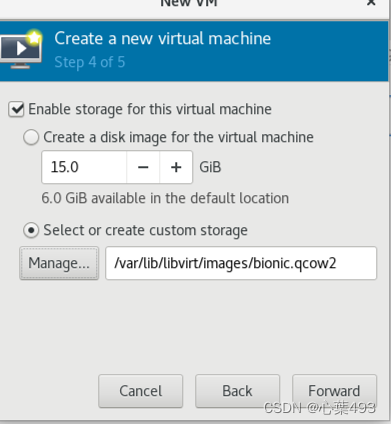
网络选项选择默认(我是NAT)
系统安装
——使用默认设置
——设置用户密码,用户名使用ubuntu,密码随意
——分区选择单ext4根分区 或者默认LVM分区亦可
——是否自动下载随意
——在安装软件选项中,选择安装openssh,也可以安装另外在openstack中需要使用的功能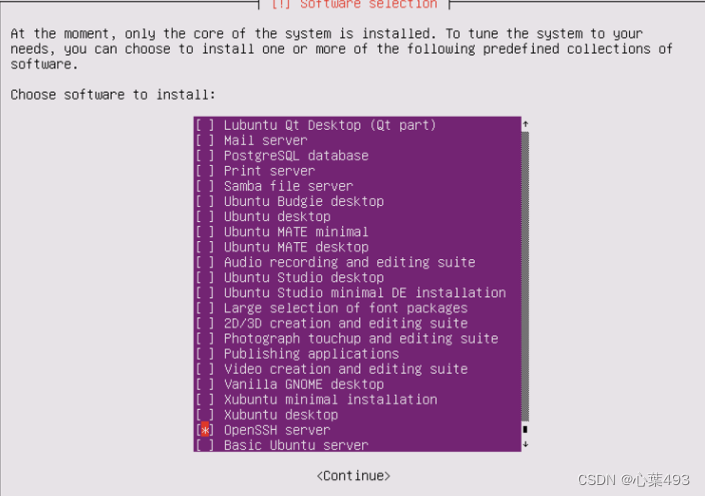
——选择安装grub选单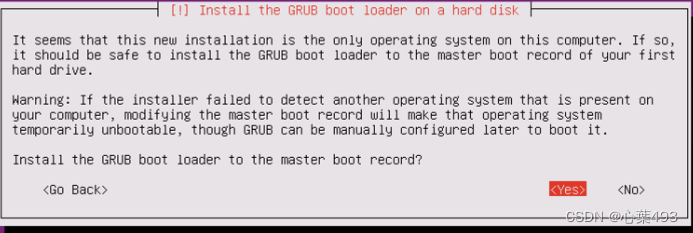
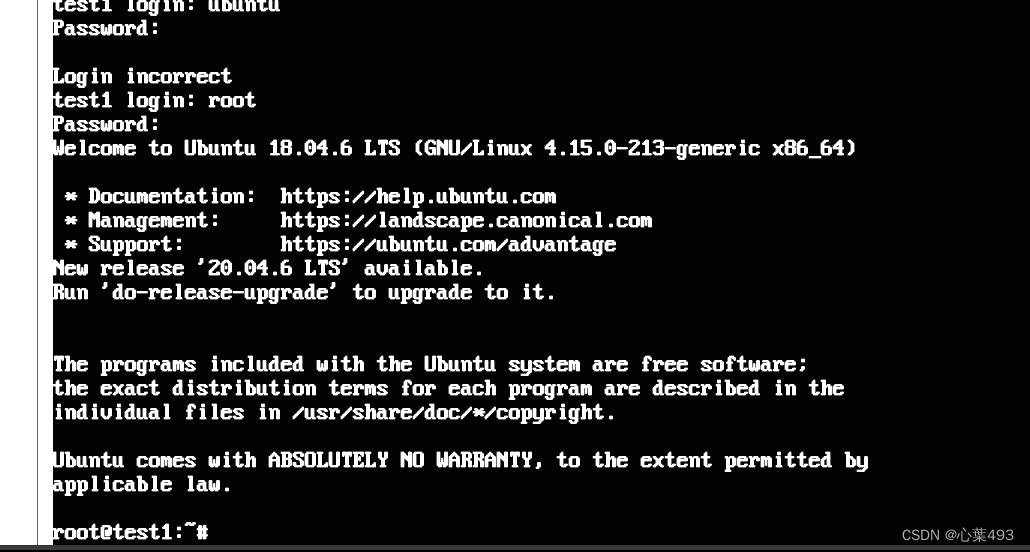
登录虚机
通过之前设置的账号密码登录
建议登录后立马改root密码,我刚两次都是装完之后输入正确密码后提示错误的

安装cloud-init
cloud-initcloud-init脚本在实例启动时启动,搜索元数据提供者以从中获取公钥,安装并将公钥放置在镜像的默认账户中,在Ubuntu中该账户就是ubuntu
它可以:
1、设置默认语⾔环境
2、设置实例主机名
3、添加 ssh keys到 .ssh/authorized_keys
4、设置⽤户密码
5、配置⽹络安装软件包
同时/var/log/cloud-init.log 会完整地记录 cloud-init 运⾏的所有细节,是 debug 最重要的⼯具。
apt install cloud-init
对cloud init进行设置
dpkg-reconfigure cloud-init
并选择EC2
通过vim /etc/cloud/cloud.cfg可以修改将密钥放在哪个user的目录下
关闭实例
su - root
/sbin/shutdown -h now
删除细节信息
删除网卡细节
#我的vm名称是ubuntu18.04
virt-sysprep -d ubuntu18.04
使虚机脱离libvirt纳管
virsh undefine ubuntu18.04
结束与验证
压缩与转移
cd /var/lib/libvirt/images/
mkdir /iso
#修改一下权限
chown root:root bionic.qcow2
virt-sparsify --compress bionic.qcow2 /iso/bionic.qcow2
#注意如果硬盘空间不足就会告警
也可以使用qemu-img convert精简置备,两个命令作用一样
qemu-img convert -c -O qcow2 bionic.qcow2 /iso/bionic.qcow2
可以看到压缩之后体积大大减少
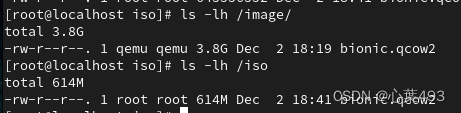
将压缩后的bionic.qcow2拿出来上传至OpenStack
验证是否能够正常运行
glance image-create --name ubuntu-bionic --disk-format qcow2 --container-format bare --visibility public --progress < /image/bionic.qcow2
创建实例,成功登录