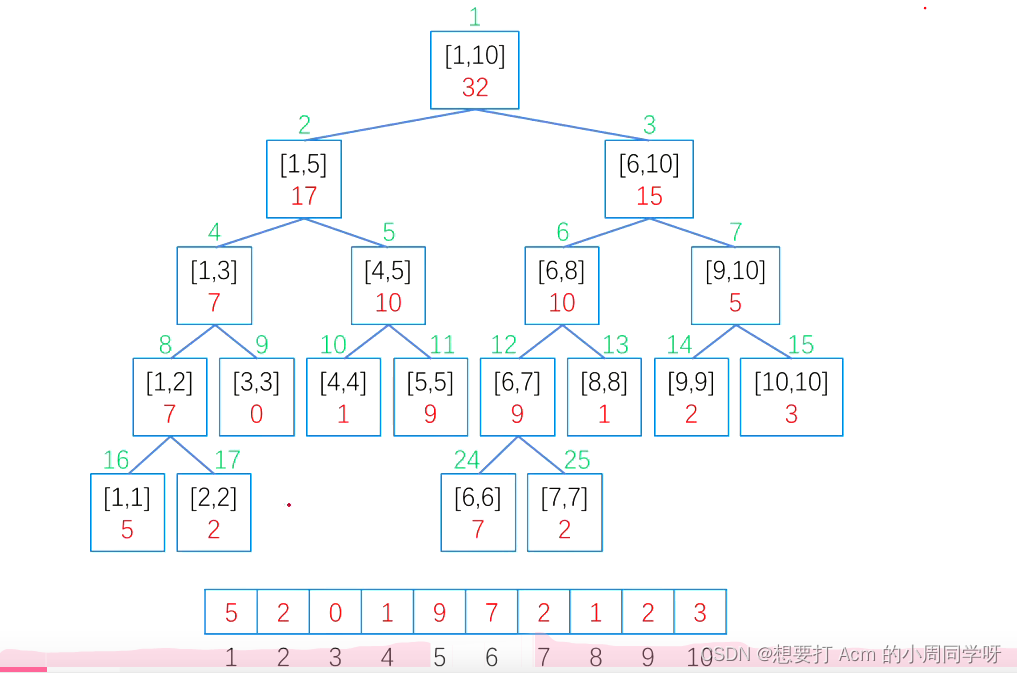
线段树的基础模板代码

#include <bits/stdc++.h>
using namespace std;
#define N 100005
#define int long long#define lc p << 1     // 2*i
#define rc p << 1 | 1 // 2*i+1int n, m;
int w[N];struct node
{int l, r, sum, add;} tr[N * 4];
// 构建线段树void pushup(int p)
{tr[p].sum = tr[lc].sum + tr[rc].sum;
}
void pushdown(int p)
{if (tr[p].add){tr[lc].sum += tr[p].add * (tr[lc].r - tr[lc].l + 1),tr[rc].sum += tr[p].add * (tr[rc].r - tr[rc].l + 1),tr[lc].add += tr[p].add,tr[rc].add += tr[p].add,tr[p].add = 0;}
}
void build(int p, int l, int r)
{tr[p] = {l, r, w[l], 0};if (l == r)return;int mid = l + r >> 1;build(lc, l, mid);build(rc, mid + 1, r);pushup(p);
}
int query(int p, int x, int y)
{ // 区查if (x <= tr[p].l && tr[p].r <= y)return tr[p].sum;int m = tr[p].l + tr[p].r >> 1;pushdown(p);int sum = 0;if (x <= m)sum += query(lc, x, y);//if (y > m)sum += query(rc, x, y);return sum;
}void update(int p, int x, int y, int k)
{// 修改区间的值'if (x <= tr[p].l && tr[p].r <= y){tr[p].sum += (tr[p].r - tr[p].l + 1) * k;tr[p].add += k;return;}int mid = tr[p].l + tr[p].r >> 1;pushdown(p); // 先下沉if (x <= mid){update(lc, x, y, k);}if (y > mid){update(rc, x, y, k);}pushup(p); // 再上乘
}// 区间修改 对于区间[4,9] 内的每个数字
signed main()
{cin >> n >> m;for (int i = 1; i <= n; i++){int x;cin >> x;w[i] = x;}build(1, 1, n);for (int i = 1; i <= m; i++){int a, x, y, k;cin >> a >> x >> y;if (a == 1){cin >> k;update(1, x, y, k);}else if (a == 2){cout << query(1, x, y) << endl;}}
}

对点进行修改，从跟节点进入，找到根节点，将根节点的值修改下

查询区间

区间修改如果直接修改容易看出来时间复杂度是on的

懒惰修改

修改上面区间的sum值，

https://ac.nowcoder.com/acm/contest/63746/A
题目，采用线段树的代码来解决问题

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define N 200005
#define lc p << 1
#define rc p << 1 | 1int n, m;
struct node
{int l, r, sum, add;} tr[N * 4];
int w[N];void pushup(int p)
{tr[p].sum = tr[lc].sum + tr[rc].sum;
}
void pushdown(int p)
{if (tr[p].add)//^异或运算 {tr[lc].add ^= tr[p].add; //tr[rc].add ^= tr[p].add;tr[lc].sum = tr[lc].r - tr[lc].l + 1 - tr[lc].sum;tr[rc].sum = tr[rc].r - tr[rc].l + 1 - tr[rc].sum;tr[p].add = 0;}
}
void build(int p, int l, int r)
{tr[p] = {l, r};if (l == r){tr[p].sum = w[l];return;}int mid = l + r >> 1;build(lc, l, mid);build(rc, mid + 1, r);pushup(p);
}int query(int p, int x, int y)
{ // 区查// 如果以及完全覆盖掉if (x <= tr[p].l && tr[p].r <= y)return tr[p].sum;int m = tr[p].l + tr[p].r >> 1; // 没有完全覆盖就裂开pushdown(p);int sum = 0; // 定义局部变量 递归进入if (x <= m)sum += query(lc, x, y);//if (y > m)sum += query(rc, x, y);return sum;
}
// 查询时不变的 修改会发生变化void update(int p, int x, int y)
{// 修改区间的值'if (x <= tr[p].l && tr[p].r <= y){// 如果符合了// 区间修改tr[p].add ^= 1;//和1进行异或取反tr[p].sum = tr[p].r - tr[p].l + 1 - tr[p].sum;return;}int mid = tr[p].l + tr[p].r >> 1;pushdown(p); // 先下沉if (x <= mid){update(lc, x, y);}if (y > mid){update(rc, x, y);}pushup(p); // 再上乘
}signed main()
{cin >> n >> m;string s;cin >> s;for (int i = 0; i < s.length(); i++){w[i + 1] = s[i] - '0';}build(1, 1, n);for (int i = 1; i <= m; i++){int a, x, y;cin >> a >> x >> y;if (a == 0){update(1, x, y);}else if (a == 1){cout << query(1, x, y) << endl;}}
}