西工大计算机学院计算机系统基础实验一（函数编写1~10）

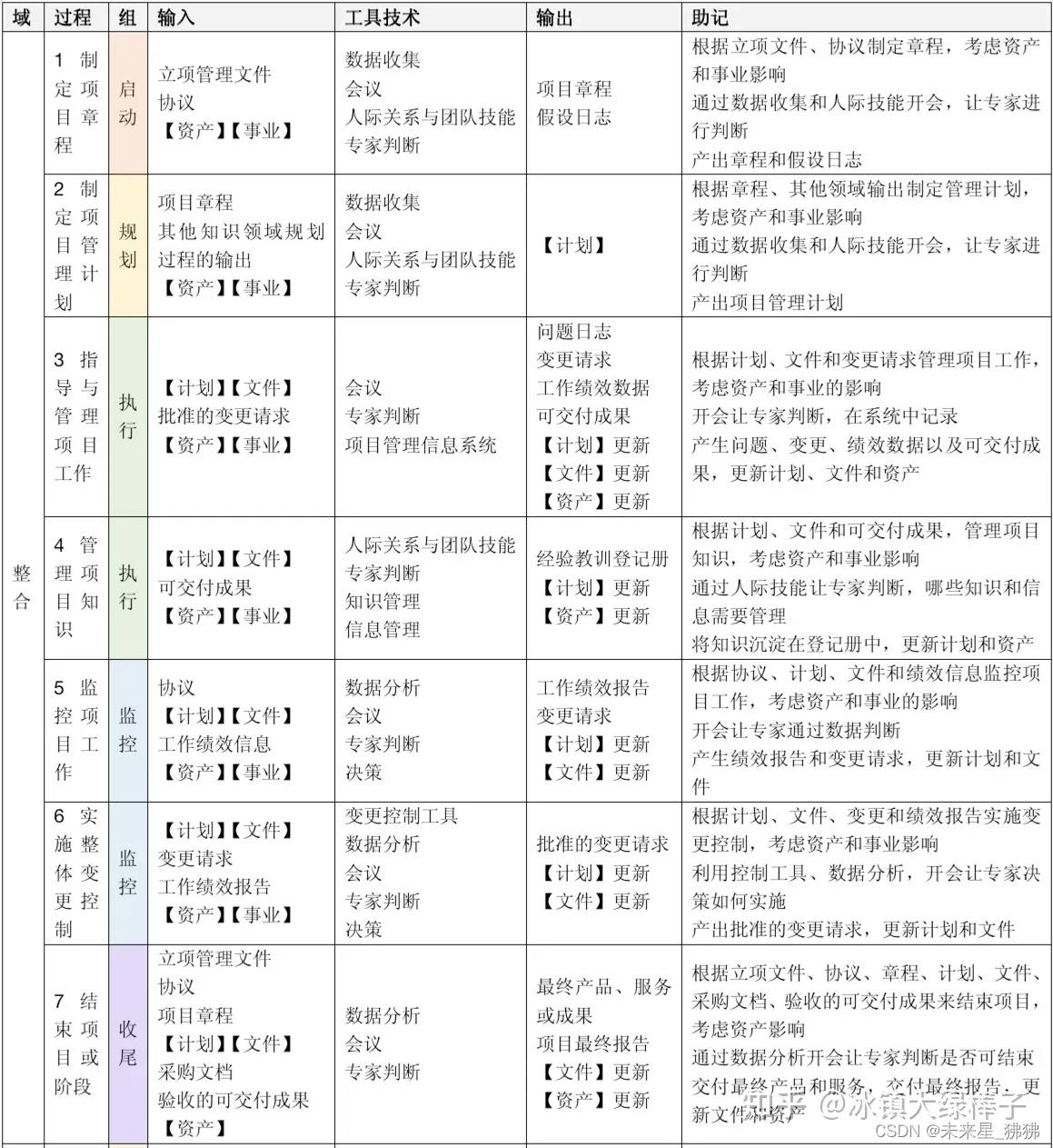
还是那句话，千万不要慌，千万不要着急，耐下性子慢慢来，一步一个脚印，把基础打的牢牢的，一样不比那些人差。回到实验本身，自从​​​​​​按照西工大计算机学院计算机系统基础实验一（环境配置）-CSDN博客 这篇博客结束完成虚拟机平台VMware 17 Workstation Pro的安装，以及Ubuntu虚拟机的导入，还有实验包的导入之后，我们看到了如下图所示的实验压缩包content_1701767947881.tar，如 图1：查看被导入到Ubuntu虚拟机的实验包的压缩包content_1701767947881.tar 所示。接着我们解压缩这个包，如 图2：解压缩实验压缩包content_1701767947881.tar 所示。

（图1：查看被导入到Ubuntu虚拟机的实验包的压缩包content_1701767947881.tar） 

 

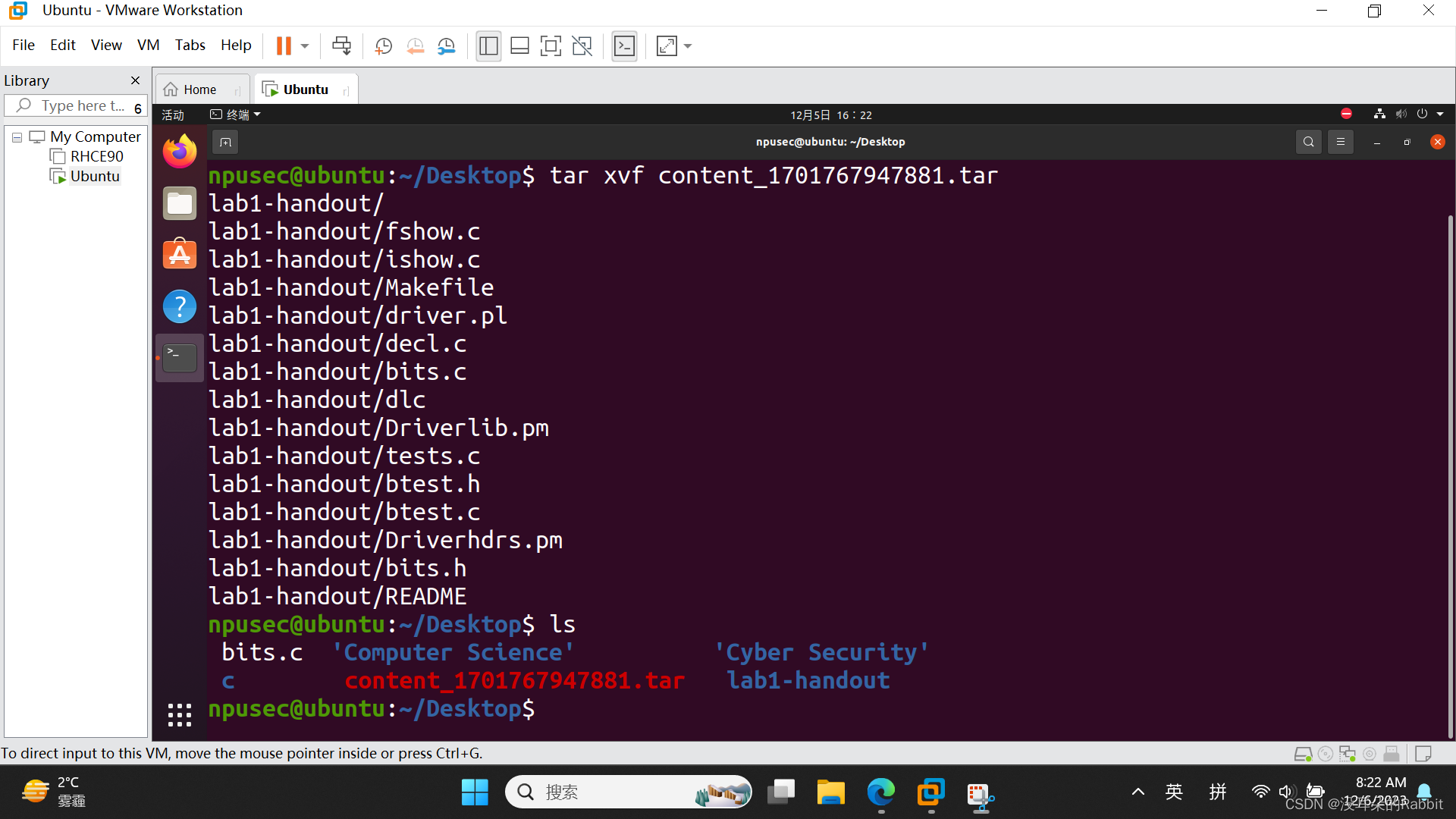
（图2：解压缩实验压缩包content_1701767947881.tar。使用"tar xvf content_1701767947881.tar"命令解压实验压缩包之后，得到了lab1-handout文件夹） 

接着进入到lab1-handout文件夹，并且查看该lab1-handout文件夹下有什么文件，如 图3：进入lab1-handout文件夹，查看该文件夹下的文件 所示。 但是千万不要急着，什么都不懂就开始做，先耐下性子来慢慢读一读README文件，了解清楚lab1-handout这个文件夹是用来干什么的，如 图4：使用less命令查看README文件 、图5：查看README文件的第一页、图6：查看README文件的第二页 所示。这其中可能有很多大家不熟悉的命令，但千万不要排斥它，跟着作者一步一步来就可以。

（图3：进入lab1-handout文件夹，查看该文件夹下的文件） 

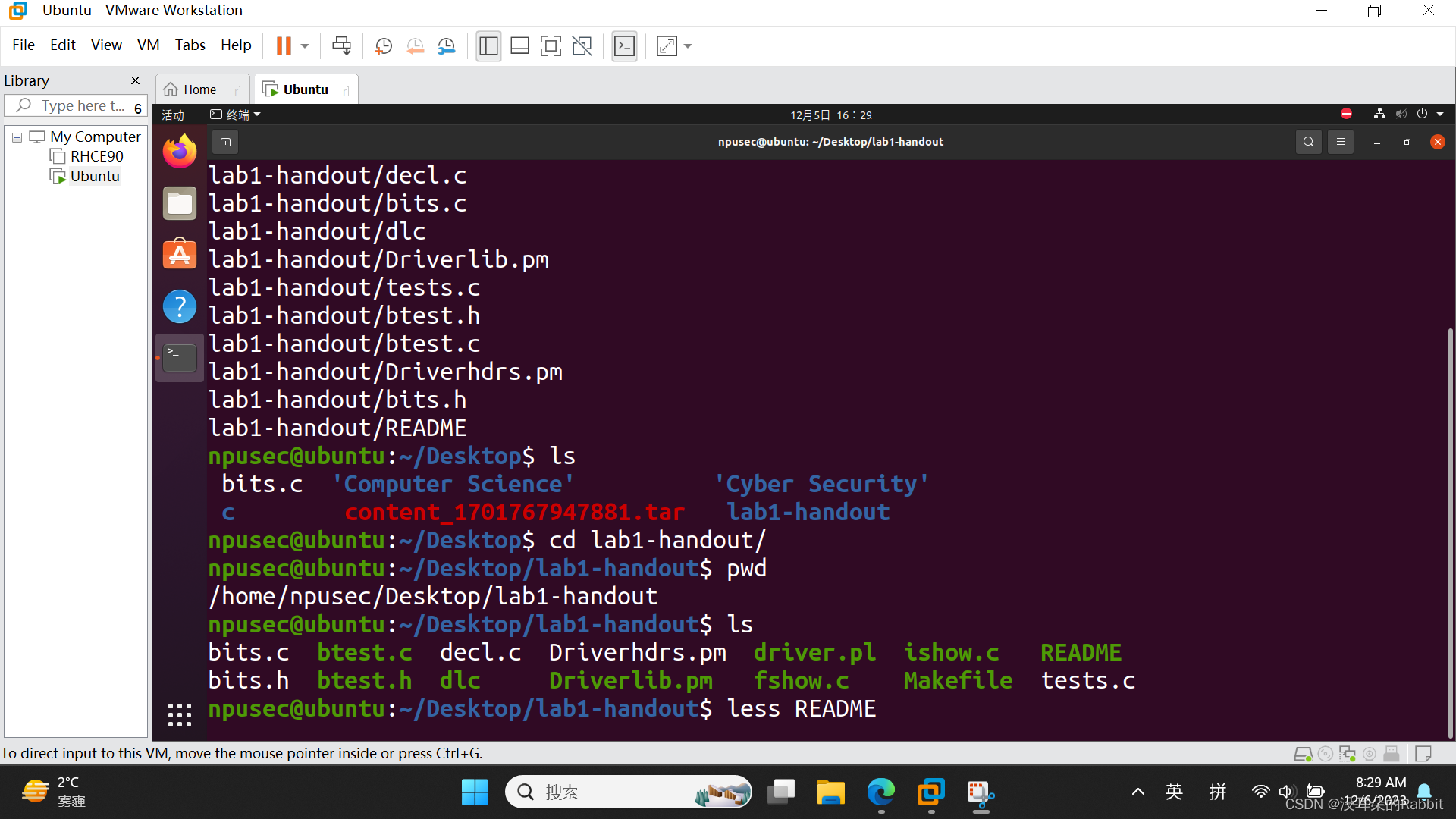
 （图4：使用less命令查看README文件）

 （图5：查看README文件的第一页）

 

 （图6：查看README文件的第二页）

在这里不要害怕怎么读，不要害怕说因为它是英文，所以就感到害怕。不要害怕，耐下性子慢慢读，就可以读出来一二的。在这里它的大概意思是，我们需要编写bits.c文件中的几个函数的函数体，接着使用dlc可执行文件检查bits.c文件中我们所写的函数是否满足运算符等的要求，然后使用make clean命令清除掉上一次已生成的可执行文件，再使用make btest文件生成可执行文件，最后运行生成的可执行文件价差我们所写的函数的正确性。你可能听不懂这段话是什么意思，不要怕，你跟着作者做，后面都会详细的讲到的。接着使用同样的方法，我们来查看bits.c文件，如 图7：查看bits.c文件（上）、图8：查看bits.c文件（下） 所示。

（图7：查看bits.c文件（上））

 （图8：查看bits.c文件（下））

 bits.c文件开头的一大段注释给我们三个要点信息：

要点1：不要使用"#include <stdio.h>"，我们可以得到要点2与要点3：

要点2：对于整型数，只能使用& ^ | + << >> ! ~这八个运算符，只能定义并使用int型的局部变量以及函数参数变量，只能使用0x0到0xFF的int型常量；

要点3：对于浮点数，只能使用& ^ | + << >> ! ~这八个运算符，可以定义并使用int型或unsigned int型的局部变量以及函数参数变量，可以使用任意有符号整型与无符号整型常量，可以使用循环与条件判断。

大家记住它就好，不要深究，考虑到有些同学的Ubuntu没有内置VS code，而且vim编辑器对于初学者来说难度也有点大，所以我们选择Ubuntu内置的文本编辑器，开始编辑bits.c中的第一个函数，如 图9：使用Ubuntu内置的文本编辑器，开始编辑bits.c中的第1个函数 所示。如果文本编辑器的大小过小，可以按照 图10：调大文本编辑器显示文字的大小（上） 、图11：调大文本编辑器显示文字的大小（下） 所示。

 （图9：使用Ubuntu内置的文本编辑器，开始编辑bits.c中的第1个函数）

（图10：调大文本编辑器显示文字的大小（上）） 

（图11：调大文本编辑器显示文字的大小（下）） 

定位到第174行，我们开始编写第一个函数bitXor，如 图12：定位到第174行，开始编写第1个函数bitXor 所示。

（图12：定位到第174行，开始编写第1个函数bitXor）

bitXor的意思是什么呢？意思是，需要我们只使用取反和位与运算，来实现异或操作。即只使用~与&，来实现^操作。那么该怎么实现这个功能呢？根据异或操作的定义，相同为0，不同才为1。也就是说，0^0=0，0^1=1，1^0=1，1^1=0。观察这个例子，我们发现，只要其中有并且只有1个为1即可。即~x&y和x&~y一个需要为1，一个需要为0，可以写成(~x&y)|(x&~y)，但是不允许使用位或操作，那么我们应该怎么做呢？再思考下去就很麻烦了。我们不妨换一种思路，当x&y与~x&~y都为0时，这时只对应着两种情况，0^1=1与1^0=1，然后对x&y和~x&~y取反，得到~(x&y)和~(~x&~y)，这时只有当0^1=1与1^0=1这两种情况下，~(x&y)和~(~x&~y)才都为1，进而~(x&y)&~(~x&~y)才为1，所以只需要写一个语句 "return ~(x&y)&~(~x&~y)"即可。如 图13：编写完成第1个函数bitXor 所示。接着保存对bits.c文件的修改，然后在包含bits.c文件的文件夹中打开命令行，如 图14：在包含bits.c文件的文件夹中打开命令行 所示。接着使用命令"./dlc -e bits.c"查看运算符的数量是否满足要求以及是否满足其它的要求。如果除了对各个函数所使用到的运算符进行计数之后就没有其它的输出，那么表明满足运算符和其它的要求。接着使用"make clean"命令清除掉上一次遗留的旧的文件，如 图15：使用命令"./dlc -e bits.c"和命令"make clean" 所示。接着再使用命令"make btest"生成新的文件，生成btest这个新的可执行文件之后，使用命令“./btest -f bitXor”来检验我们所写的第一个函数bitXor的正确性，其中"-f"选项制定了需要被检验的函数名，在这里需要被检验的函数名是bitXor。如 图16：使用命令"make btest"和命令“./btest -f bitXor” 所示。我们已成功编写了bitXor函数。

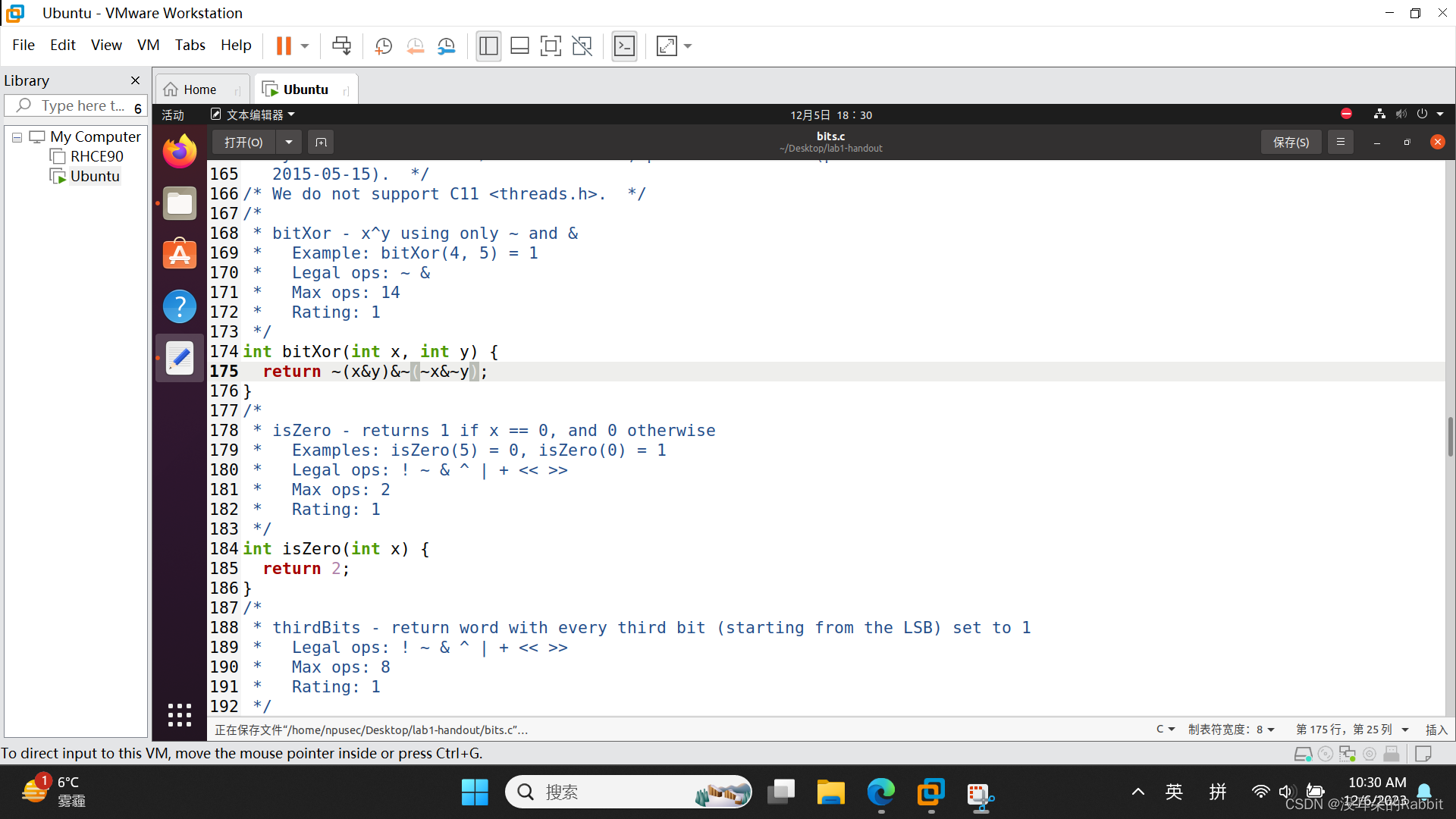
（图13：编写完成第1个函数bitXor） 

（图14：在包含bits.c文件的文件夹中打开命令行） 

（图15：使用命令"./dlc -e bits.c"和命令"make clean" 。使用命令"./dlc -e bits.c"查看运算符的数量是否满足要求以及是否满足其它的要求。如果除了对各个函数所使用到的运算符进行计数之后就没有其它的输出，那么表明满足运算符和其它的要求。接着使用"make clean"命令清除掉上一次遗留的旧的文件） 

 

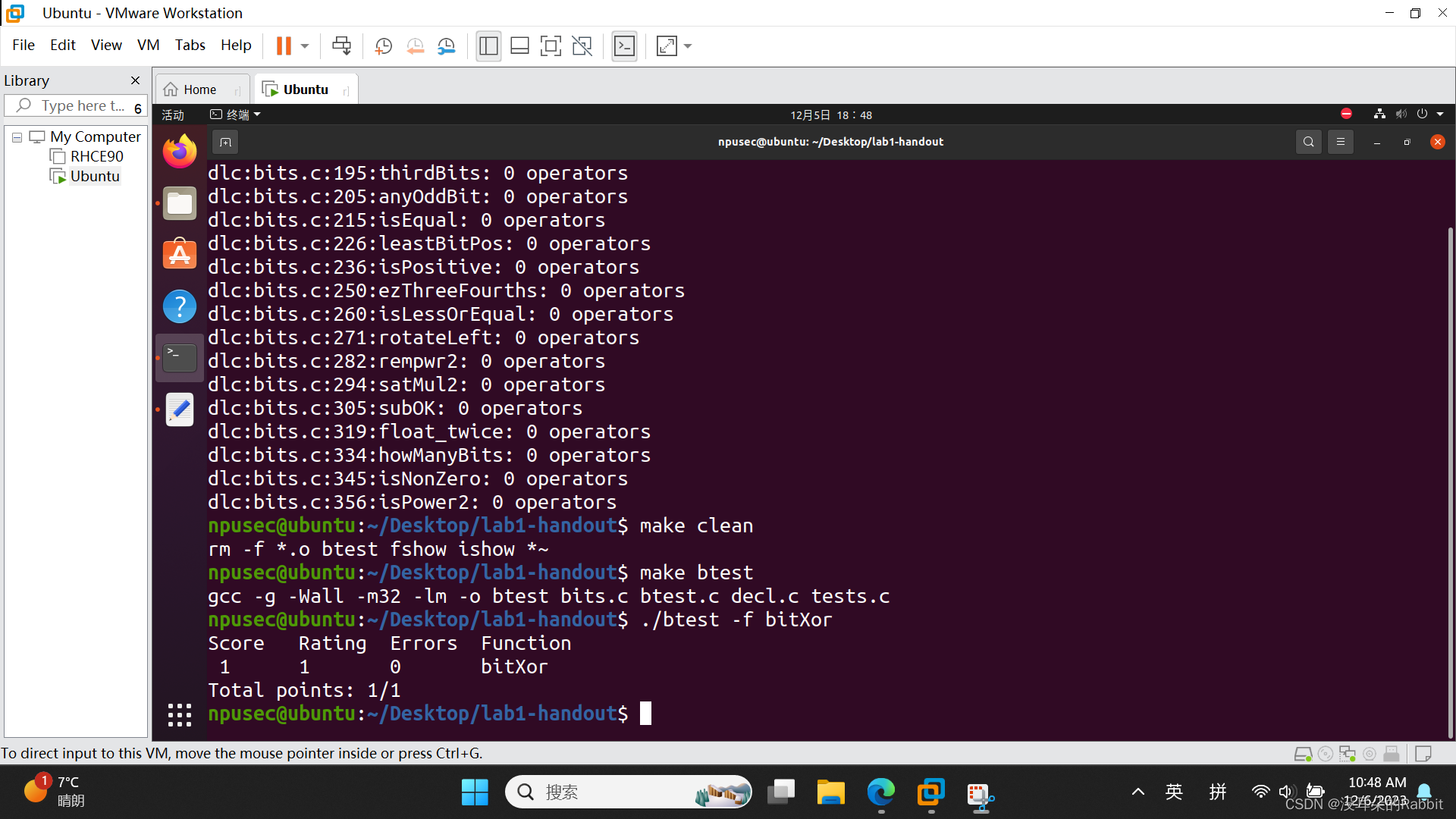
 （图16：使用命令"make btest"和命令“./btest -f bitXor”）

 接着第二个函数，isZero，当x为0时，返回1，当x不为0时，返回0，所以只需要简单的写"return !x"即可，如 图17：编写第2个函数isZero 和 图18：重复编写第1个函数时的操作 所示。

（图17：编写第2个函数isZero）

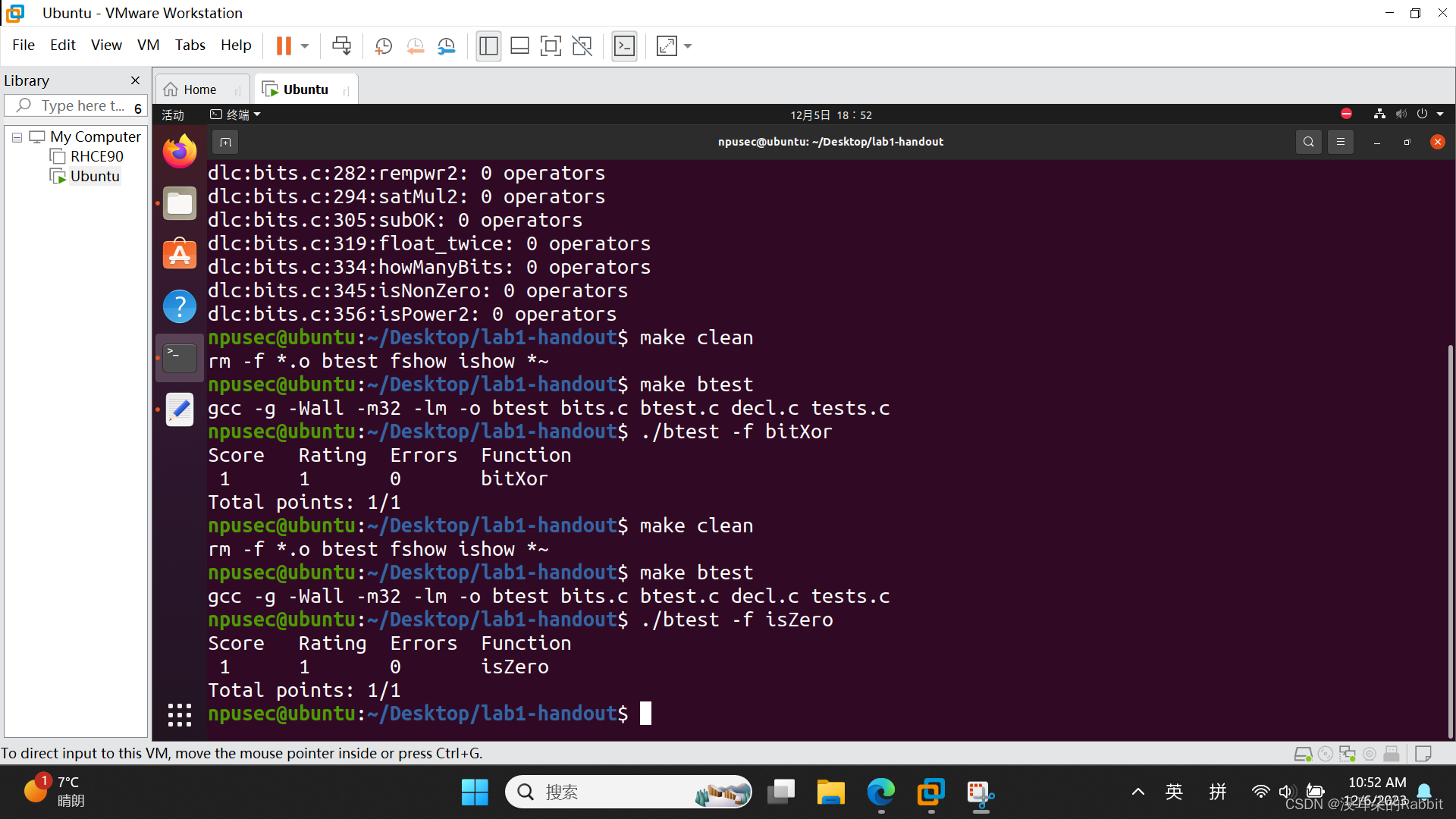
 （图18：重复编写第1个函数时的操作。使用命令"./dlc -e bits.c"统计各个函数使用到的运算符的个数，使用命令"make clean"清除掉上一次遗留下来的旧的可执行文件，使用命令"make btest"生成新的btest可执行文件，使用命令"./btest -f isZero"检验所写函数isZero的正确性）

第三个函数，thirdBits，要我们自己产生一个int型的数，保证它从最低有效位开始，每第三个比特位被设置为1，即期望我们返回的数是：0100 1001 0010 0100 1001 0010 0100 1001B。但是根据要点二中的一句话：只能使用0x0到0xFF的int型常量，即我们不能直接返回它。那么应该怎么产生这个数呢？我们发现，可以先产生一个小于0xFF的int型常量，让它既满足从最低有效位开始，每第三个比特位被设置为1，又满足小于0xFF，而这个数就是0x49，它的二进制表示形式为0100 1001。接着让0x49左移9位，得到了1001 0010 0000 0000，左移9位的目的就是为了让其既能保证，除了低9位以外，从最低有效位开始，每第三个比特位被设置为1，又是0x49左移所能完成这个任务的极限。接着将0x49与0x49<<9拼凑在一起，得到了0000 0000 0000 0000 1001 0010 0100 1001，它结合了0x49和0x49<<9的优点，保证了最大程度上从最低有效位开始，每第三个比特位被设置为1。但是，最高的16个比特位还没有被处理，而这可以简单的通过((0x49<<9)+0x49)<<18来实现。最后将0x49、0x49<<9与((0x49<<9)+0x49)<<18拼凑起来，即为最终的答案。而为了节省运算符，我们使用int型变量t来保存((0x49<<9)+0x49)，接着"return t+(t<<24)"即可。具体的五个步骤为：

  1. 期望的输出: 0100 1001 0010 0100 1001 0010 0100 1001

  2. 第一个步骤: 0000 0000 0000 0000 0000 0000 0100 1001 0x49

  3. 第二个步骤: 0000 0000 0000 0000 1001 0010 0000 0000 0x49<<9

  4. 第三个步骤: 0000 0000 0000 0000 1001 0010 0100 1001 (0x49<<9)+0x49

  5. 第四个步骤: 0100 1001 0010 0100 0000 0000 0000 0000 ((0x49<<9)+0x49)<<18

  6. 第五个步骤: 0100 1001 0010 0100 1001 0010 0100 1001 (((0x49<<9)+0x49)<<18)+(0x49<<9)+0x49

如 图19：编写第3个函数thirdBits 所示。

 （图19：编写第3个函数thirdBits）

第4个函数anyOddBit，如果x中，只要有一个第奇数个比特位被设置为了1，那么就返回1，否则返回0，比如7是0111，其第0、1、2个比特位为1，满足第1个比特位被设置为1，返回1；比如5是0101，第0、2个比特位为1，不满足第奇数个比特位被设置为1，也就是第1个比特位没有被设置为1，所以返回0，注意这里特别容易混淆，作者因为搞混了这一点，废了好多功夫。我们的思路就是，先产生1010 1010 1010 1010 1010 1010 1010 1010，这个数是0xAAAAAAAA，它第1、3、5、7、9、11... ...31个比特位都被设置为了1，然后将0xAAAAAAAA与x做位与操作，这样子获取x的所有奇数比特位，如果x中存在一个奇数比特位被设置为1，那么位与的结果就不为0，此时连用两个逻辑非!，即可得到1，如果x中所有奇数比特位都是0，那么位与的结果就是0，此时连用两个逻辑非!，即可得到0。那么我们该如何得到0xAAAAAAAA呢？可以按照下面的五个步骤来得到0xAAAAAAAA。为了节省运算符，引入int a=0xAA，int b=0xAA<<8，int c=a+b，int d=(c<<16)+c，这时d即为0xAAAAAAAA。然后编写第四个函数anyOddBit，如 图20：编写第4个函数anyOddBit 所示。

  1. 期望的输出: 1010 1010 1010 1010 1010 1010 1010 1010 0xAAAAAAAA

  2. 第一个步骤: 0000 0000 0000 0000 0000 0000 1010 1010 0xAA

  3. 第二个步骤: 0000 0000 0000 0000 1010 1010 0000 0000 0xAA<<8

  4. 第三个步骤: 0000 0000 0000 0000 1010 1010 1010 1010 (0xAA<<8)+0xAA

  5. 第四个步骤: 1010 1010 1010 1010 0000 0000 0000 0000 ((0xAA<<8)+0xAA)<<16

  6. 第五个步骤: 1010 1010 1010 1010 1010 1010 1010 1010 (((0xAA<<8)+0xAA)<<16)+((0xAA<<8)+0xAA)

（图20：编写第4个函数anyOddBit） 

第5个函数，isEqual，如果两个int型数相等，那么返回1，否则返回0，我们直接!(x^y)即可。如 图21：编写第5个函数isEqual 所示。

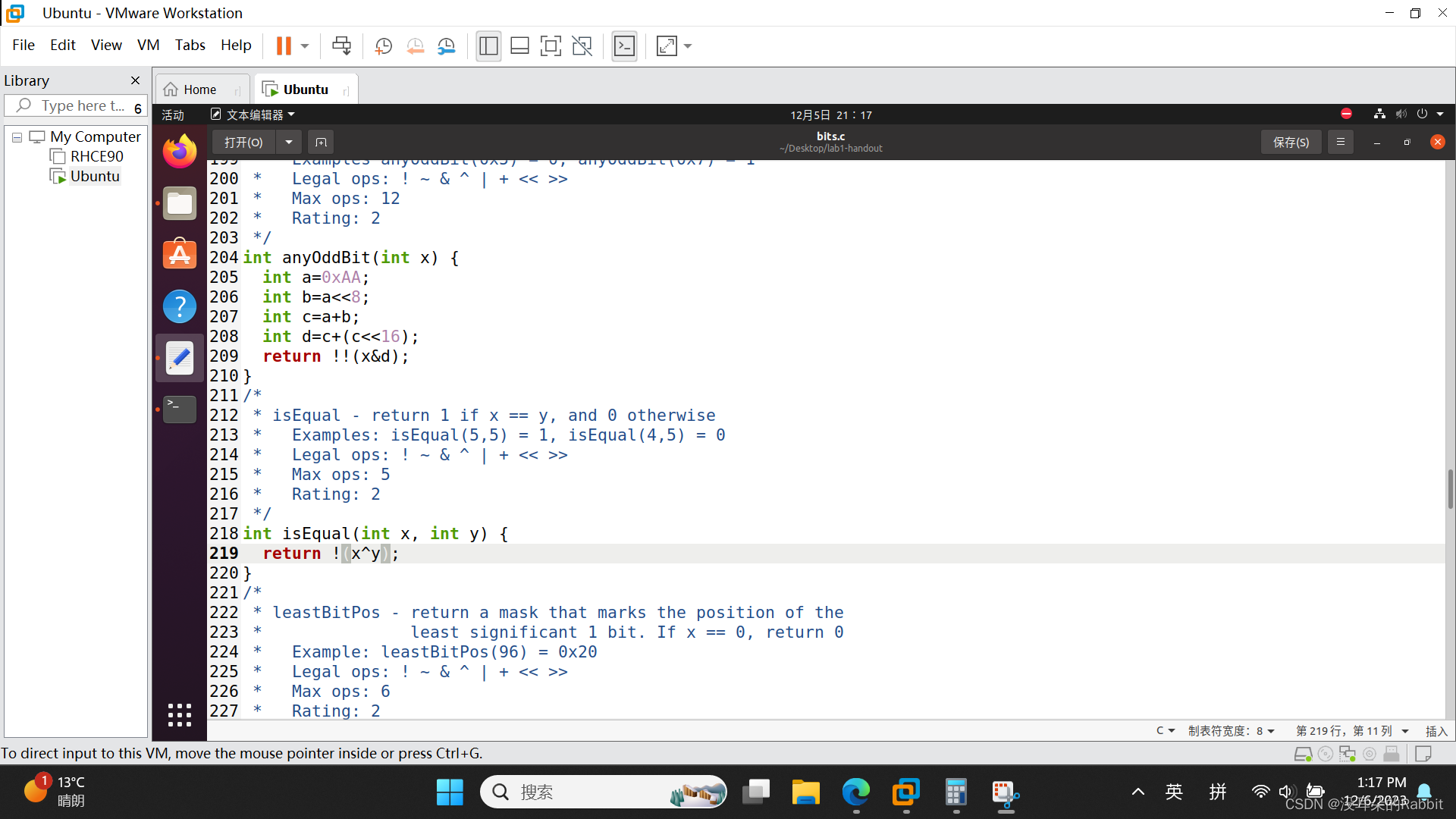
（图21：编写第5个函数isEqual） 

第6个函数，leastBitPos，可以理解为，找到从左到右最后一个1的位置，然后其它位置都设为0。对于96来说，96可以写成0110 0000，最低位的1是从右往左第5个，所以返回0010 0000；对于104来说，104可以写成0110 1000，从左到右最后一个1的位置是第3个，所以返回0000 1000。那么我们该怎么做呢？发现可以将x各位取反然后加1，并将这个结果与x进行位与，这时返回的结果即为我们期望中的结果。比如对于96，也就是0110 0000来说，各位取反得到了1001 1111，再加1得到了1010 0000，然后将这个数与0110 0000进行位与操作，得到了0010 0000，正好是我们想要的结果，所以我们"return ((~x)+1)&x;"即可，如 图22：编写第6个函数leastBitPos 所示。

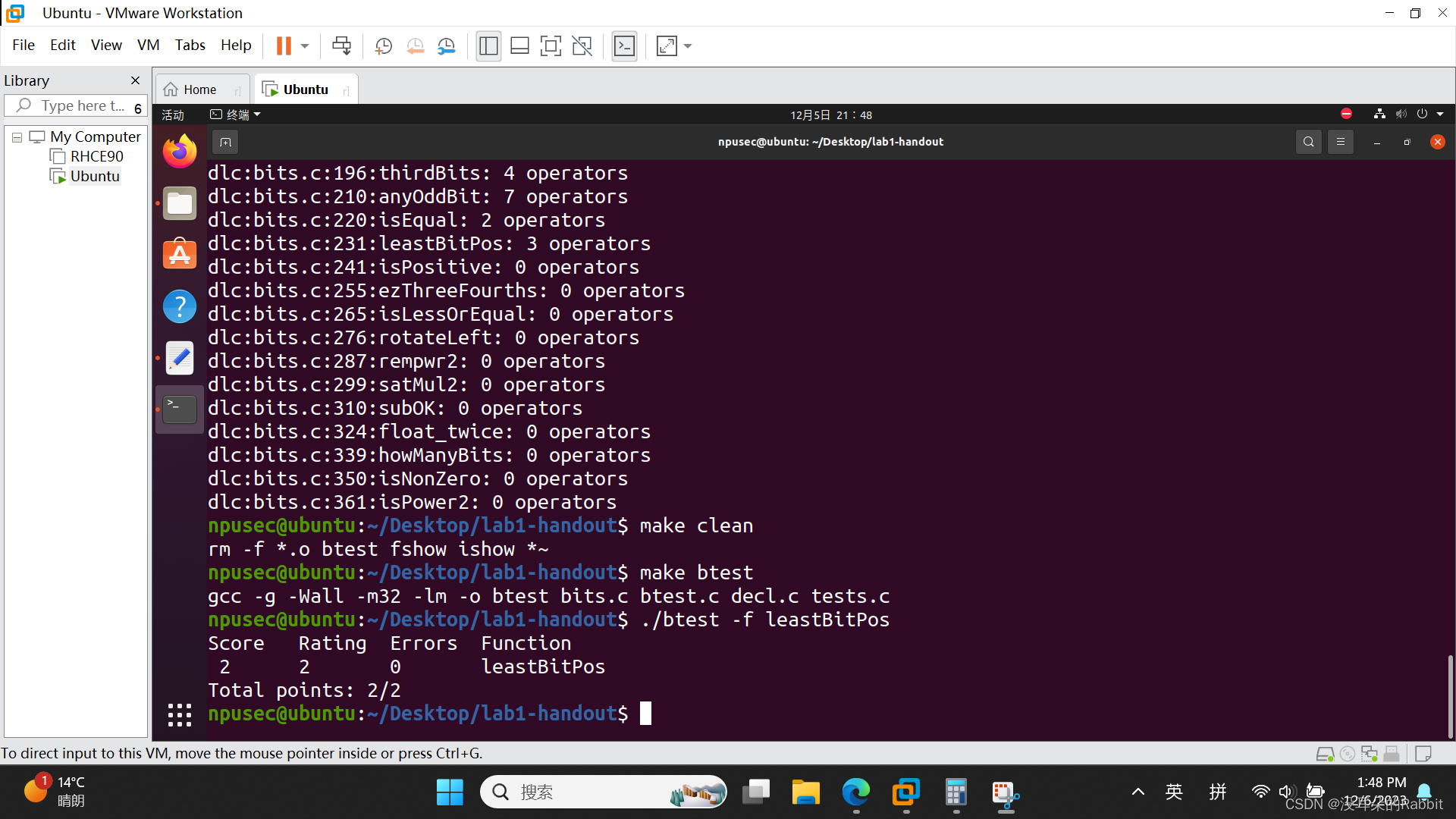
（图22：编写第6个函数leastBitPos）

接着第7个函数，isPositive， 如果x大于0的话返回1，如果x不大于0的话返回0。该怎么做呢？只需要判断符号位即可。该怎么获取符号位呢？可以将x右移31位，因为一方面针对int型变量的右移都是算术右移，另外一方面实验也规定了所有的右移都是算术右移，所以我们将x右移31位，这样所有的比特位都和符号位是一样的取值了。这时得到!(x>>31)，如果x为正，则符号位为0，x>>31为0，逻辑非后为1；如果x为负，则符号位为1，x>>31为0xFFFFFFFF，逻辑非后为0。另外考虑到当x为0时，本想让其返回0，结果此时!(x>>31)的结果也是1，所以需要修正，修正的结果为!(x>>31)&!!x，进而可以写成!(!x|x>>31)。当x为0时，!x为1，!x|x>>31直接为1，!(!x|x>>31)为0；当x为负数时，!x为0，x>>31为0xFFFFFFFF，!(!x|x>>31)为0；当x为正数时，!x为0，x>>31也为0，进而!(!x|x>>31)为1，按照这个思路，我们写出了"return !(!x|x>>31)"，如 图23：编写第7个函数isPositive 所示。

（图23：编写第7个函数isPositive） 

第8个函数，ezThreeFourths，开始慢慢变复杂了，我们需要完美复现C语言表达式x*3/4，那么该怎么做呢？首先计算x*3，x*3可以用位运算表示为(x<<1)+x，接着计算x/4，这里并不能简单的((x<<1)+x)>>2。为什么呢？因为如果简单的这样做以后，会存在当x为负数时舍入的问题，比如当x=-1、-2、-3、-5、-6、-7... ...时，((x<<1)+x)>>2会比x*3/4小1，而当x=-4、-8、-12时，((x<<1)+x)>>2才会与x*3/4相等。所以为了解决这个问题，进行修正，设a=(x<<1)+x，修正为(a+(a>>31)&0x3)>>2，这样子就可以啦！如 图24：编写第8个函数ezThreeFourths 所示。

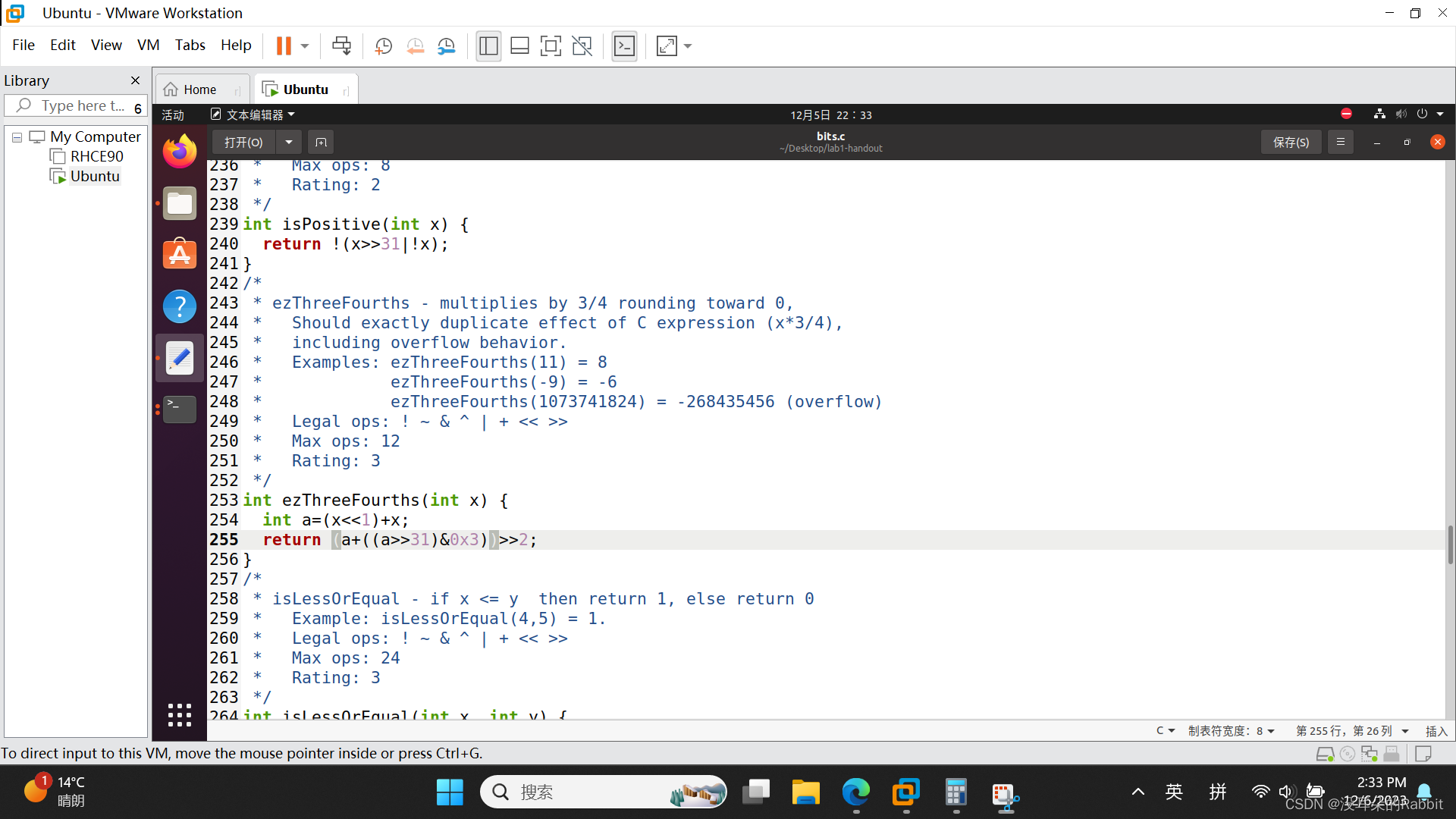
(图24：编写第8个函数ezThreeFourths)

第9个函数，isLessOrEqual。首先从大方向上来看，存在一个或的情况，也就是说，当x等于y时也返回1，所以大框架为：

(                                                       ) | (    !(x^y)    )

这样子解决了或的问题，下一步就应该要解决isLess的问题。怎么解决这个问题呢？第一反应是通过计算x-y=x+~y+1，根据结果的符号位来判断是否小于。但问题在于，虽然一般情况下这种方法是对的，但如果是一个很小的负数减去一个很大的正数，或者一个很大的正数减去一个很小的负数，这时int类型就无法表示相减的结果，甚至无法表示1-0x8000 0000的结果。所以就需要根据int类型能不能放得下相减的结果，来进行分类讨论。那么如何判断int类型能不能放得下相减的结果呢？我们发现，只有当x与y异号时才存在溢出的问题，所以我们可以将x与y是否同号作为分类依据，这样子大框架进一步细分为：

((    (x^~y)&(            )    |    (        )   ) >>31)&1 | (    !(x^y)    )

当x与y同号时，x与~y异号，x^~y的符号位为1，此时x-y的符号位为即为我们想返回的结果，所以直接返回x-y即可，这时大框架即为：

((    (x^~y)&(x+~y+1)    |    (        )   ) >>31)&1 | (    !(x^y)    )

而当x与y异号时，x与~y同号，x^~y的符号位为0，此时选择x&~y，如果x符号位为0，那么x一定大于y，最终应该返回0，而x&~y恰好就是0；如果x符号位为1，那么x一定小于y，最终应该返回1，而x&~y恰好就是1。利用这个性质，最终的大框架即可完成：

((    (x^~y)&(x+~y+1)    |    (     x&~y   )   ) >>31)&1 | (    !(x^y)    )

而如果只选择直接看x的符号位是否为1，而不是选择x&~y的话，有可能出现x与y同号并且x-y符号位为0并且x符号位为1，这时(x^~y)&(x+~y+1)符号位为0，x符号位为1，0|1为1，返回1，但我们想要其返回0，这就出现了冲突。为了避免这个冲突，就需要保证当x与y同号，x^~y的符号位为1时，我们选择的表达式一定为0，所以这才选择了x&~y。有些同学会问，那我们最开始的时候，为什么不写成(           !!(x^y)&()                                            ) | (    !(x^y)    )，是不是也是这个道理呢？对。因为当!(x^y)为1，即x==y时，!!(x^y)&()中的()一定为0，所以我们才选择省略了!!(x^y)。最终，如 图25：编写第9个函数isLessOrEqual 所示。

（图25：编写第9个函数isLessOrEqual）

 第10个函数，rotateLeft，将x旋转左移n位。比如0x87654321左移4位得到了0x76543218，该怎么得到0x76543218呢？我们发现，其由两部分组成，分别是0x76543210与0x8。0x76543210可直接由x<<4得到，0x8可有x>>28然后与0xF做位与得到。最终4可被n代替，28可被32+~n+1代替，那么如何得到0xF呢？最省运算符的方法是，~0+(1<<n)。所以按照这个思路，我们可写出表达式为"(x<<n)|((x>>(32+~n+1))&(~0+(1<<n)))"，最终如 图26：编写第10个函数rotateLeft 所示。

（图26：编写第10个函数rotateLeft）

/* * bitXor - x^y using only ~ and & *   Example: bitXor(4, 5) = 1*   Legal ops: ~ &*   Max ops: 14*   Rating: 1*/
int bitXor(int x, int y) {return ~(x&y)&~(~x&~y);
}
/** isZero - returns 1 if x == 0, and 0 otherwise *   Examples: isZero(5) = 0, isZero(0) = 1*   Legal ops: ! ~ & ^ | + << >>*   Max ops: 2*   Rating: 1*/
int isZero(int x) {return !x;
}
/* * thirdBits - return word with every third bit (starting from the LSB) set to 1*   Legal ops: ! ~ & ^ | + << >>*   Max ops: 8*   Rating: 1*/
int thirdBits(void) {int t=0x49+(0x49<<9);return t+(t<<18);
}
/* * anyOddBit - return 1 if any odd-numbered bit in word set to 1*   Examples anyOddBit(0x5) = 0, anyOddBit(0x7) = 1*   Legal ops: ! ~ & ^ | + << >>*   Max ops: 12*   Rating: 2*/
int anyOddBit(int x) {int a=0xAA;int b=a<<8;int c=a+b;int d=c+(c<<16);return !!(x&d);
}
/* * isEqual - return 1 if x == y, and 0 otherwise *   Examples: isEqual(5,5) = 1, isEqual(4,5) = 0*   Legal ops: ! ~ & ^ | + << >>*   Max ops: 5*   Rating: 2*/
int isEqual(int x, int y) {return !(x^y);
}
/* * leastBitPos - return a mask that marks the position of the*               least significant 1 bit. If x == 0, return 0*   Example: leastBitPos(96) = 0x20*   Legal ops: ! ~ & ^ | + << >>*   Max ops: 6*   Rating: 2 */
int leastBitPos(int x) {return ((~x)+1)&x;
}
/* * isPositive - return 1 if x > 0, return 0 otherwise *   Example: isPositive(-1) = 0.*   Legal ops: ! ~ & ^ | + << >>*   Max ops: 8*   Rating: 2*/
int isPositive(int x) {return !(x>>31|!x);
}
/** ezThreeFourths - multiplies by 3/4 rounding toward 0,*   Should exactly duplicate effect of C expression (x*3/4),*   including overflow behavior.*   Examples: ezThreeFourths(11) = 8*             ezThreeFourths(-9) = -6*             ezThreeFourths(1073741824) = -268435456 (overflow)*   Legal ops: ! ~ & ^ | + << >>*   Max ops: 12*   Rating: 3*/
int ezThreeFourths(int x) {int a=(x<<1)+x;return (a+((a>>31)&0x3))>>2;
}
/* * isLessOrEqual - if x <= y  then return 1, else return 0 *   Example: isLessOrEqual(4,5) = 1.*   Legal ops: ! ~ & ^ | + << >>*   Max ops: 24*   Rating: 3*/
int isLessOrEqual(int x, int y) {
return ((((((x+~y+1)&(x^~y))|(x&~y))>>0x1f))&1)|!(x^y);
}
/* * rotateLeft - Rotate x to the left by n*   Can assume that 0 <= n <= 31*   Examples: rotateLeft(0x87654321,4) = 0x76543218*   Legal ops: ~ & ^ | + << >> !*   Max ops: 25*   Rating: 3 */
int rotateLeft(int x, int n) {return (x<<n)|((x>>(32+~n+1))&(~0+(1<<n)));
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/211617.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

决策树 （人工智能期末复习）

决策树 （人工智能期末复习）

几个重要概念 信息熵&#xff1a;随机事件未按照某个属性的不同取值划分时的熵减去按照某个属性的不同取值划分时的平均 熵。即前后两次熵的差值。 表示事物的混乱程度&#xff0c;熵越大表示混乱程度越大&#xff0c;越小表示混乱程度越小。 对于随机事件&#xff0c;如果它的…
阅读更多...
Python实现广义线性回归模型(statsmodels GLM算法)项目实战

Python实现广义线性回归模型(statsmodels GLM算法)项目实战

说明&#xff1a;这是一个机器学习实战项目&#xff08;附带数据代码文档视频讲解&#xff09;&#xff0c;如需数据代码文档视频讲解可以直接到文章最后获取。 1.项目背景 广义线性模型(Generalized Linear Model&#xff0c;简称GLM)是一种广泛应用于回归分析和分类问题的统…
阅读更多...
python炒股自动化（1），量化交易接口区别

python炒股自动化（1），量化交易接口区别

要实现股票量化程序化自动化&#xff0c;就需要券商提供的API接口&#xff0c;重点是个人账户小散户可以申请开通&#xff0c;上手要简单&#xff0c;接口要足够全面&#xff0c;功能完善&#xff0c;首先&#xff0c;第一步就是要找对渠道和方法&#xff0c;这里我们不讨论量化…
阅读更多...
IDEA快速生成lambda表达式的方法

IDEA快速生成lambda表达式的方法

IDEA快速生成lambda表达式的方法-CSDN博客 建议修改成 shift/
阅读更多...
吴恩达《机器学习》11-1-11-2:首先要做什么、误差分析

吴恩达《机器学习》11-1-11-2:首先要做什么、误差分析

一、首先要做什么 选择特征向量的关键决策 以垃圾邮件分类器算法为例&#xff0c;首先需要决定如何选择和表达特征向量 &#x1d465;。视频提到的一个示例是构建一个由 100 个最常出现在垃圾邮件中的词构成的列表&#xff0c;根据这些词是否在邮件中出现来创建特征向量&…
阅读更多...
鸿蒙4.0开发笔记之ArkTS语法基础之条件渲染和循环渲染的使用（十五）

鸿蒙4.0开发笔记之ArkTS语法基础之条件渲染和循环渲染的使用（十五）

文章目录 一、条件渲染&#xff08;if&#xff09;二、循环渲染&#xff08;ForEach&#xff09; 一、条件渲染&#xff08;if&#xff09; 1、定义 正如其他语言中的if…else…语句&#xff0c;ArkTS提供了渲染控制的能力&#xff0c;条件渲染可根据应用的不同状态&#xff0…
阅读更多...
Linux安装MySQL

Linux安装MySQL

更新密钥 rpm --import https://repo.mysql.com/RPM-GPG-KEY-mysql-2022安装Mysql yum库 rpm -Uvh http://repo.mysql.com//mysql57-community-release-el7-7.noarch.rpmyum安装Mysql yum -y install mysql-community-server设置开机自启 systemctl start mysqld systemctl…
阅读更多...
React立即更新DOM

React立即更新DOM

正常情况下&#xff0c;react会等待set完毕后再进行页面渲染&#xff0c;所以在set时无法拿到更新后的dom import { useRef, useState } from "react"export default () > {const div useRef(null)const [count, setCount] useState(0)const btnClick () >…
阅读更多...
怎么检测电脑电源？电脑电源检测系统软件如何助力？

怎么检测电脑电源？电脑电源检测系统软件如何助力？

电源是电脑的重要组成部分&#xff0c;为电脑提供稳定电源&#xff0c;保证电脑正常工作。但是在电脑实际使用过程中总会遇到各种各样的问题和故障&#xff0c;比如无法开机&#xff0c;因此电脑电源检测是非常重要的测试内容。 如何测试电脑电源? 1. 用万用表检测 a. 将万用表…
阅读更多...
【Qt之QSqlRelationalTableModel】描述及使用

【Qt之QSqlRelationalTableModel】描述及使用

描述 QSqlRelationalDelegate链接: https://blog.csdn.net/MrHHHHHH/article/details/134690139 QSqlRelationalTableModel类为单个数据库表提供了一个可编辑的数据模型&#xff0c;并支持外键。 QSqlRelationalTableModel的行为类似于QSqlTableModel&#xff0c;但允许将列设…
阅读更多...
MySQL根据binlog恢复数据

MySQL根据binlog恢复数据

简介 本文介绍了使用mysqlbinlog导出数据&#xff0c;根据binlog恢复数据&#xff0c;和导出数据时报需要super权限的解决方法。 环境 MySQL: 5.7.40 说明 MySQL的binlog是数据库服务器在运行过程中产生的日志文件&#xff0c;记录了数据库增删改的操作&#xff0c;可用于恢复和…
阅读更多...
【理解ARM架构】中断处理 | CPU模式

【理解ARM架构】中断处理 | CPU模式

&#x1f431;作者&#xff1a;一只大喵咪1201 &#x1f431;专栏&#xff1a;《理解ARM架构》 &#x1f525;格言&#xff1a;你只管努力&#xff0c;剩下的交给时间&#xff01; 目录 &#x1f35c;中断&#x1f368;GPIO中断代码实现 &#x1f35c;CPU&#x1f368;CONTROL…
阅读更多...
docker集群的详解以及超详细搭建

docker集群的详解以及超详细搭建

文章目录 一、问题引入1. 多容器位于同一主机2. 多容器位于不同主机 二、介绍三、特性四、概念1. 节点nodes2. 服务(service)和任务(task)3. 负载均衡 五、docker网络1. overlay网络 六、docker集群搭建1. 环境介绍2. 创建集群3. 集群网络4. 加入工作节点 七、部署可视化界面po…
阅读更多...
MYSQL数据库中运行SQL文件报错

MYSQL数据库中运行SQL文件报错

报错显示 当使用mysql数据库运行SQL文件报错时 [Err] 1273 - Unknown collation: utf8mb4_0900_ai_ci 报错原因 版本高低问题&#xff0c;一个是5.7版本&#xff0c;一个是8.0版本生成转储文件的数据库版本为8.0,要导入sql文件的数据库版本为5.7,因为是高版本导入到低版本&a…
阅读更多...
ThermalLabel SDK for .NET 13.0.23.1113 Crack

ThermalLabel SDK for .NET 13.0.23.1113 Crack

ThermalLabel SDK for .NET 是一个 .NET 典型类库&#xff0c;它允许用户和开发人员创建非常创新的条码标签并将其发布在 zebra ZPL、EPL、EPSON ESC、POS 以及 Honeywell intermec 指纹中通过在 VB.NET 或 C# 上编写 .NET 纯代码来实现热敏打印机&#xff0c;以实现项目框架的…
阅读更多...
通过仿真理解信道化接收机分析过程

通过仿真理解信道化接收机分析过程

概要 信道化从子信道带宽划分上可分为临界抽取和非临界抽取两种&#xff0c;从各子信道中心频率布局上可分为偶型排列和奇型排列&#xff0c;从处理流程上可分为信道化分析与信道化综合过程。本文主要通过仿真来理解偶型排列/临界抽取/信道化分析过程。 基本原理 常规的数字…
阅读更多...
音频修复和增强软件iZotope RX 10 mac特点介绍

音频修复和增强软件iZotope RX 10 mac特点介绍

iZotope RX 10 mac是一款音频修复和增强软件&#xff0c;主要特点包括&#xff1a; 声音修复&#xff1a;iZotope RX 10可以去除不良噪音、杂音、吱吱声等&#xff0c;使音频变得更加清晰干净。 音频增强&#xff1a;iZotope RX 10支持对音频进行音量调节、均衡器、压缩器、限…
阅读更多...
人工智能_机器学习053_支持向量机SVM目标函数推导_SVM条件_公式推导过程---人工智能工作笔记0093

人工智能_机器学习053_支持向量机SVM目标函数推导_SVM条件_公式推导过程---人工智能工作笔记0093

然后我们再来看一下支持向量机SVM的公式推导情况 来看一下支持向量机是如何把现实问题转换成数学问题的. 首先我们来看这里的方程比如说,中间的黑线我们叫做l2 那么上边界线我们叫l1 下边界线叫做l3 如果我们假设l2的方程是上面这个方程WT.x+b = 0 那么这里 我们只要确定w和…
阅读更多...
软考高项第四版五组十域表+ITTO背诵笔记及助记

软考高项第四版五组十域表+ITTO背诵笔记及助记

基于第四版做的笔记&#xff0c;助记是自己编的 还是得靠理解记忆&#xff0c;下面是文档&#xff0c;也用anki制作了记忆卡片&#xff0c;需要的可以自行导入卡包
阅读更多...
慎用！3个容易被打的Python恶搞脚本

慎用！3个容易被打的Python恶搞脚本

Python 无限恶搞朋友电脑&#xff0c;别提有多爽了&#xff0c;哈哈&#xff0c;打造自己的壁纸修改器&#xff0c;电脑无限锁屏&#xff0c; 无线弹窗&#xff0c;都在这里&#xff01;&#xff01;&#xff01; 1、修改电脑桌面壁纸 工具使用 开发环境&#xff1a;python3…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023