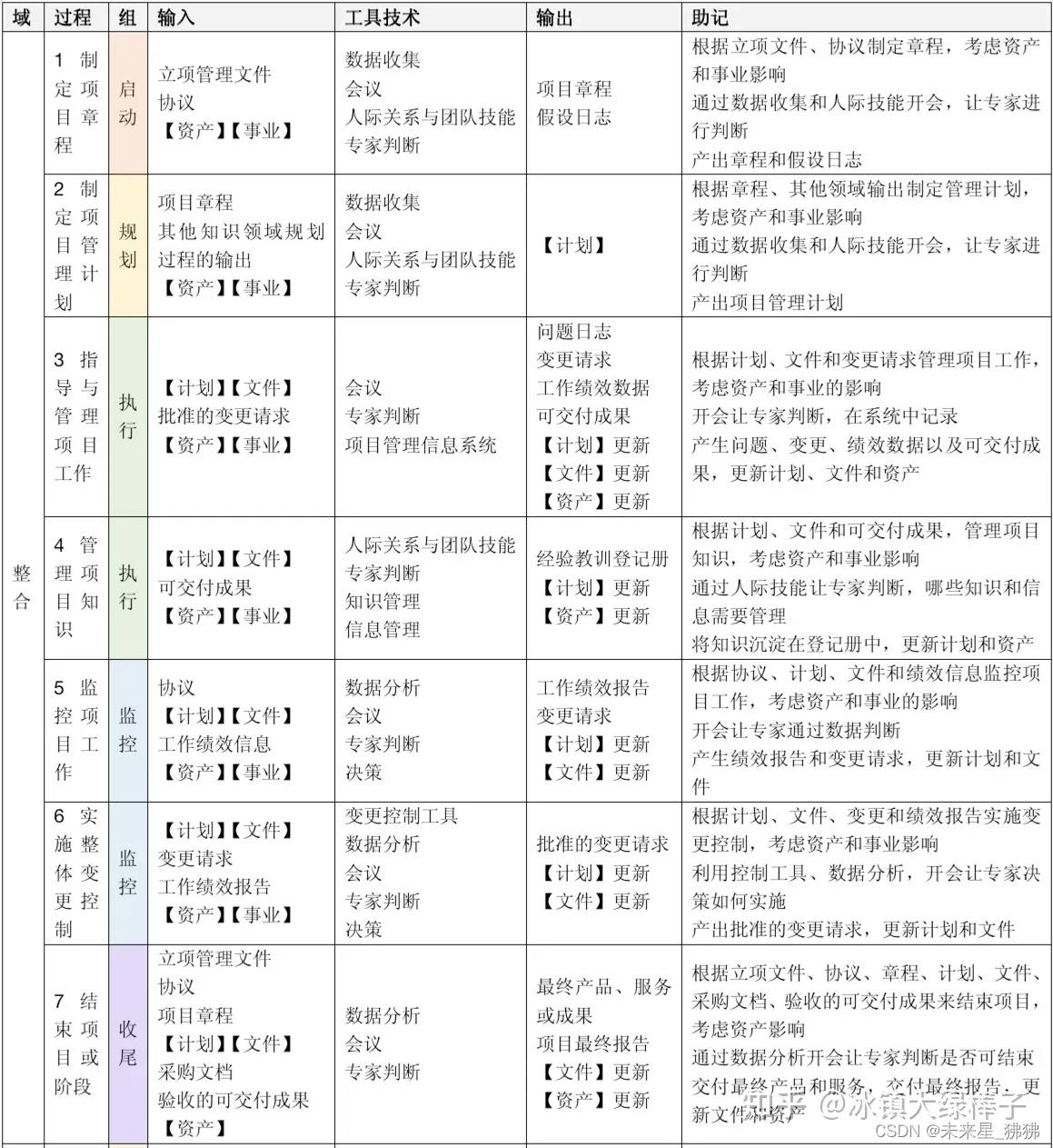
几个重要概念
-
信息熵:随机事件
未按照某个属性的不同取值划分时的熵减去按照某个属性的不同取值划分时的平均
熵。即前后两次熵的差值。
表示事物的混乱程度,熵越大表示混乱程度越大,越小表示混乱程度越小。
对于随机事件,如果它的取值有N种情况,每种情况发生的概率为P,那么这件事的熵为:
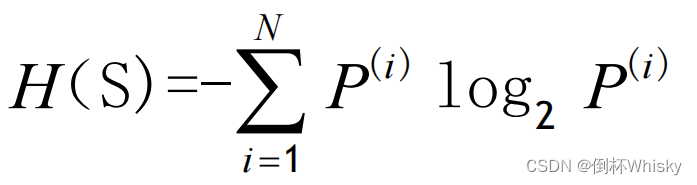
-
信息增益:
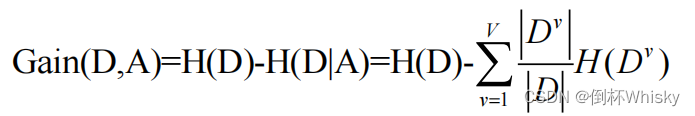
-
信息增益率:
使用信息增益比上训练数据集D关于特征A的值的熵
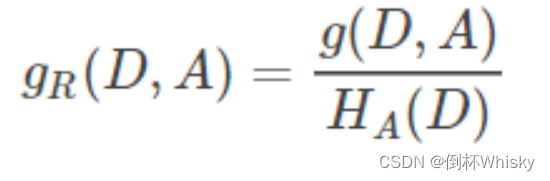
-
基尼系数
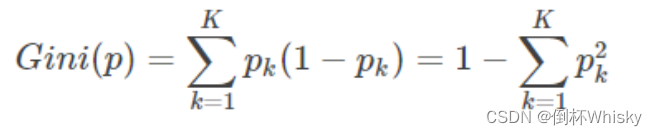
例题
其实主要还是背公式+计算不出错,等我考完另一门试再写。
(20年)设训练集如下表所示,请用经典的 ID3 算法完成其学习过程。

(19年)下表给出外国菜是否有吸引力的数据集,每个菜品有 3 个属性“温度”、“口味”,“份量”,请用决策树算法画出决策树(根据信息增益)。并预测 dish= {温度=热,口味=甜,份量=大} 的一道菜,是否具有吸引力。

(18年)下表为是否适合打垒球的决策表,请用决策树算法画出决策树,并请预测 E= {天气=晴,温度=适中,湿度=正常,风速=弱} 的场合,是否合适打垒球。

(17年)设使用ID3算法进行归纳学习的输入实例集S={ i | 1≤ i ≤ 7 }如下表所示。学习的目标是用属性A、B、C预测属性F。
(1)写出集合S分别以属性A、B、C作为测试属性的熵的增益Gain(S, A)、Gain(S, B)、Gain(S, C)的表达式。
(2)属性A、B、C中哪个应该作为决策树根节点的测试属性?

考虑下面一个数据集,它记录了某学生多次考试的情况,请根据提供的数据按要求构建决策树。
(1)根据信息增益率选择第一个属性,构建一个深度为1的决策树(根结点深度为1)。
(2)根据信息增益率构建完整的决策树。请回答,这两个决策树的决策结果是否和训练数据一致,并解释说明。

设样本集合如下表格,其中A、B、C是F的属性,请根据信息增益标准(ID3算法),画出F的决策树。