【算法每日一练]-图论（保姆级教程篇12 tarjan篇）#POJ3352道路建设 #POJ2553图的底部 #POJ1236校园网络 #缩点

今天知识点

加边使得无向图图变成双连通图

找出度为0的强连通分量

加边使得有向图变成强连通图

将有向图转成DAG图进行dp

POJ3352：道路建设

思路：

POJ2553：图的底部

思路：

POJ1236校园网络

思路：

缩点：

思路：

POJ3352：道路建设

由于道路要维修，维修时候来回都不能走，现要在各个景点间建设新道路以便维修时候也能保证任何两个景点之间可以相互到达，求最少的新道路数量
任何一对景点间最多只能在它们之间有一条道路(没有重边)。道路一开始是联通的

输入：
3 3
1 2
2 3
1 3
或
10 12
1 2
1 3
1 4
2 5
2 6
5 6
3 7
3 8
7 8
4 9
4 10
9 10

思路：

先求解边双连通分量，然后缩点，然后通过加边再把新图变成双连通图。

加边原理是这样的：
先统计叶节点个数为k，(k+1)/2就是要建的边数。因为在树中，给叶节点加边一定会产生环

说一下tarjan后的操作

for(int u=1;u<=n;u++)for(int i=head[u];i;i=e[i].next){int v=e[i].to;if(low[u]!=low[v]) deg[low[u]]++;//遍历新图的边（其实就是旧图的桥）
//有重边也要记录。low[u]就是连通分量号，每个连通分量中只有桥的点才有度}int leaf=0;
//		for(int i=1;i<=n;i++){
//			cout<<i<<' '<<deg[i]<<' '<<low[i]<<'\n';//看详情
//		}for(int i=1;i<=n;i++){//检查每个连通分量号的度（一定不为零）if(deg[i]==1) leaf++;//度是1就是叶子}cout<<(leaf+1)/2<<'\n';

首先是缩点：low是连通分量号，把度(无向图没有入度出度之分)统计到桥点身上（很像并查集中的缩点到祖宗点身上），注意我们这种缩点的过程肯定会遇到重边。此题中的重边是不能去掉的，否则叶节点会统计错误！！！

然后统计度为1就是叶子就行。

对于重边：有时候必须要，有时候不影响，有时候也必须去重。要仔细分析！

#include <bits/stdc++.h>//无向图的桥
using namespace std;
const int maxn=1000+5;
int n,m;
int head[maxn],cnt;
struct node{int to,next;}e[maxn*2];
int low[maxn],dfn[maxn],deg[maxn],num;//deg是度(无向图没有入度和出度之分)void add(int u,int v){ e[++cnt]=(node){v,head[u]};head[u]=cnt;}void tarjan(int u,int fa){dfn[u]=low[u]=++num;//初始化for(int i=head[u];i;i=e[i].next){int v=e[i].to;if(v==fa) continue;//不可以走父子边回去if(!dfn[v]){//没访问过就递归访问tarjan(v,u);low[u]=min(low[u],low[v]);//low是自己或子孙能走回的最小dfn}else{//可以从非父子边回去就要获取dfn值，就是该点能回到的最小dfnlow[u]=min(low[u],dfn[v]);}}
}void init(){memset(head,0,sizeof(head));memset(low,0,sizeof(low));memset(dfn,0,sizeof(dfn));memset(deg,0,sizeof(deg));cnt=num=0;
}int main(){while(cin>>n>>m){init();int u,v;while(m--){cin>>u>>v;add(u,v);add(v,u);}tarjan(1,0);//求边双连通分量for(int u=1;u<=n;u++)for(int i=head[u];i;i=e[i].next){int v=e[i].to;//遍历新图的边（其实就是旧图的桥）if(low[u]!=low[v]) deg[low[u]]++;
//有重边也要记录。low[u]就是连通分量号，每个连通分量中只有桥的点才有度}int leaf=0;
//		for(int i=1;i<=n;i++){
//			cout<<i<<' '<<deg[i]<<' '<<low[i]<<'\n';//看详情
//		}for(int i=1;i<=n;i++){//检查每个连通分量号的度（一定不为零）if(deg[i]==1) leaf++;//度是1就是叶子}cout<<(leaf+1)/2<<'\n';}	
}

POJ2553：图的底部

有向图中若v可以到的任何一个u，u也可以到v，则v是一个sink点，图的底部是由所有sink点构成的，按顺序输出所有sink点编号，没有sink就输出一个空行

输::
3 3
1 3 2 3 3 1
2 1
1 2
0

思路：

你只需要输出出度为0的连通分量中的所有点编号即可。

DAG图的出度为0的节点相当于终点

for(int u=1;u<=n;u++)for(int i=head[u];i;i=e[i].next){//对所有边进行判断是不是连接着两个分量int v=e[i].to;if(be[u]!=be[v]){//有重边out[be[u]]++;//缩点}}
int f=1;
for(int i=1;i<=n;i++){if(!out[be[i]]){//输出出度为0的连通分量中的点if(f) f=0;else cout<<" ";//一个数前面有个空格cout<<i; }
}

不同于无向图，有向图的连通分量号我们用一个be数组存起来

然后对所有边进行判断是不是连接着两个分量，然后对新树中的边统计出度，输出出度为0的连通分量中的点

#include <bits/stdc++.h>
using namespace std;
const int maxn=5050;
bool ins[maxn];//标记是否在栈中
int n,m;
int head[maxn],be[maxn],out[maxn];//be是属于哪个连通分量，out是缩点的出度
int low[maxn],dfn[maxn],num,id,cnt;
stack <int> s;
struct node{int to,next;}e[maxn*2];void add(int u,int v){ e[++cnt]=(node){v,head[u]};head[u]=cnt;}void tarjan(int u){dfn[u]=low[u]=++num;//dfn访问序号，low是能走回到的最早的dfnins[u]=1;s.push(u);//第一次访问节点时候入栈for(int i=head[u];i;i=e[i].next){int v=e[i].to;if(!dfn[v]){//没访问过就递归访问tarjan(v);low[u]=min(low[u],low[v]);//获取孩子的最小的low值   }else if(ins[v]){//已经访问过且在栈中获取dfn号low[u]=min(low[u],dfn[v]);}}if(low[u]==dfn[u]){//low[u]==dfn[u]时，则从栈中不断弹出节点，直到x出栈停止。弹出的节点就是同一个连通分量的int v;do{//一定要先执行再判断v=s.top();s.pop();be[v]=id;//把这些弹出的点标记同一个id号(连通分量号)ins[v]=0;}while(v!=u);//直到是自己为止id++;}
}void init(){memset(head,0,sizeof(head));memset(low,0,sizeof(low));memset(ins,0,sizeof(ins));memset(dfn,0,sizeof(dfn));memset(out,0,sizeof(out));memset(be,0,sizeof(be));cnt=num=0;id=1;
}int main(){while((cin>>n)&&n){//点数cin>>m;//边数init();int u,v;while(m--){cin>>u>>v;add(u,v);}for(int i=1;i<=n;i++){if(!dfn[i]) tarjan(i);//有向图}for(int u=1;u<=n;u++)for(int i=head[u];i;i=e[i].next){int v=e[i].to;if(be[u]!=be[v]){//有重边out[be[u]]++;//缩点}}int f=1;for(int i=1;i<=n;i++){if(!out[be[i]]){//输出出度为0的连通分量中的点if(f) f=0;else cout<<" ";//（输出格式罢了，不用在乎这里）cout<<i; }}}	
}

POJ1236校园网络

每所学校都有一份发学校名单。计算至少先发给多少个学校才能使软件传到所有学校(任务1)，计算至少增加多少扩展才能将软件发给任意学校结果都能传到所有学校(扩展就是将新成员引入一所学校的接收者名单)
5
2 4 3 0
4 5 0
0
0
1 0

思路：

任务1：每一个入度为0的连通分量都必须收到一个软件，计算个数。
任务2：每个连通分量必须既有入度也有出度，即入度为0的连通分量必须扩展一下，出度为0的连通分量必须也扩展一下（入度和出度对接，输出max就行）

DAG图中入度为0的点相当于起点

#include <bits/stdc++.h>//有向图的强连通分量
using namespace std;
const int maxn=5050;
bool ins[maxn];
int n,m,cnt;
int head[maxn],be[maxn],in[maxn],out[maxn];//be是属于哪个连通分量  in,out是每个连通分量的入度和出度
int low[maxn],dfn[maxn],num,id;
stack <int> s;
struct node{int to,next;}e[maxn*2];void add(int u,int v){ e[++cnt]=(node){v,head[u]};head[u]=cnt;}void tarjan(int u){dfn[u]=low[u]=++num;//dfn访问序号，low是能走回到的最早的dfnins[u]=1;s.push(u);//第一次访问节点时候入栈for(int i=head[u];i;i=e[i].next){int v=e[i].to;if(!dfn[v]){//没访问过就递归访问tarjan(v);low[u]=min(low[u],low[v]);//获取孩子的最小的low值   }else if(ins[v]){//已经访问过且在栈中获取dfn号low[u]=min(low[u],dfn[v]);}}if(low[u]==dfn[u]){//low[u]==dfn[u]时，则从栈中不断弹出节点，直到x出栈停止。弹出的节点就是同一个连通分量的int v;id++;do{//一定要先执行再判断v=s.top();s.pop();be[v]=id;//把这些弹出的点标记同一个id号(连通分量号)ins[v]=0;}while(v!=u);//直到是自己为止}
}int main(){cin>>n;int v;//n为学校数量for(int i=1;i<=n;i++){while(cin>>v&&v)add(i,v);//表示接收i的v学校，以0结尾}for(int i=1;i<=n;i++){if(!dfn[i]) tarjan(i);}for(int u=1;u<=n;u++)for(int i=head[u];i;i=e[i].next){int v=e[i].to;if(be[u]!=be[v]){//有重边，可以输出一下in[be[v]]++;out[be[u]]++;//统计入度和出度，来缩点}}if(id==1){//一共只要一个连通分量的话要特判cout<<1<<'\n';cout<<0<<'\n';return 0;}int ans1=0,ans2=0;//for(int i=1;i<=n;i++)cout<<i<<' '<<be[i]<<'\n';for(int i=1;i<=id;i++){//	cout<<i<<" in"<<' '<<in[i]<<" , "<<"out"<<' '<<out[i]<<'\n';if(!in[i]) ans1++;if(!out[i]) ans2++;}cout<<ans1<<'\n';cout<<max(ans1,ans2)<<'\n';	
}

缩点：

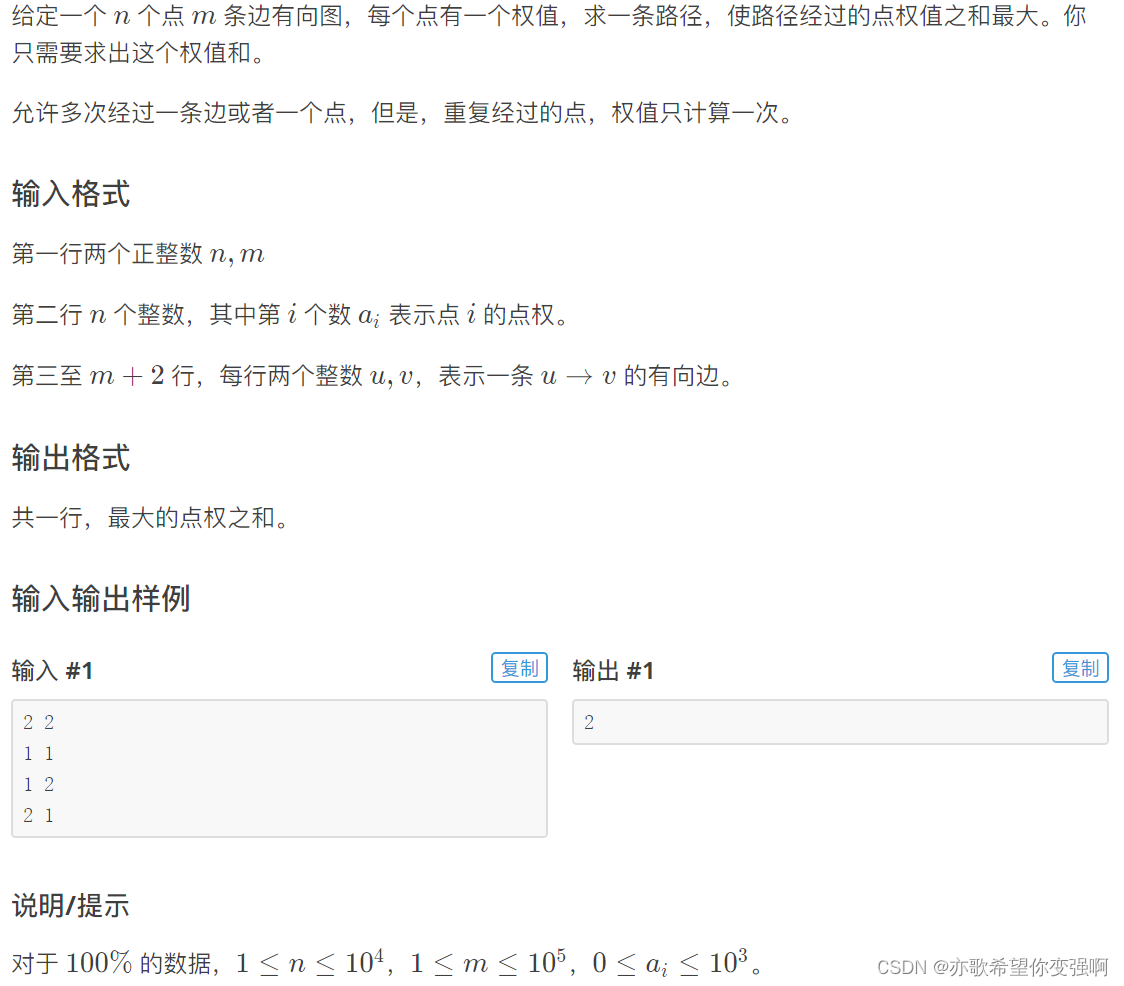
思路：

有向图中的强连通分量中的所有权值一定要全部加上，所以缩点建出新的DAG图，然后转化成了每个点走一次求最大点权值和
设置dp[v]表示到v点的最大权值和。 dp[v]=max(dp[u])即可，也就是要先求dp[u]再求dp[v]，topo排序求一边就行了。完了！

	if(low[u]==dfn[u]){//low[u]==dfn[u]时，则从栈中不断弹出节点，直到x出栈停止。弹出的节点就是同一个连通分量的int v;	do{//一定要先执行再判断v=s.top();s.pop();be[v]=u;//把这些弹出的点标记同一个id号(连通分量号)ins[v]=0;if(u==v)break;//自己不要和自己加p[u]+=p[v];}while(v!=u);//直到是自己为止}

首先是缩点操作，要把该连通分量中点的权值加给连通分量点自己(类似无向图的桥点)，

for (int i=1;i<=m;i++)//遍历每个边{int u=be[e[i].from],v=be[e[i].to];//from是起点，to是终点if (u!=v)//不同的分量号点间进行建边，有重边也不影响topo结果{newe[++tt]=(node){v,hh[u],u};hh[u]=tt;in[v]++;//建新边过程，相当于add功能}}

然后是给新DAG图建边，以便后面topo。

完整代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn=10000+15;
int n,m,tot,head[maxn],tt,hh[maxn],p[maxn];//p是每个点的权值,head和tot和e是原图的，hh和tt和newe是新图的
int num,low[maxn],dfn[maxn],ins[maxn],be[maxn];//be是每个所属的连通分量号
int in[maxn],dp[maxn];
stack<int>s;
struct node{int to,next,from;}e[maxn*10],newe[maxn*10];void add(int u,int v){e[++tot]=(node){v,head[u],u};head[u]=tot;}void tarjan(int u){dfn[u]=low[u]=++num;//dfn访问序号，low使能回溯到的最早的dfnins[u]=1;s.push(u);//第一次访问节点时候入栈for(int i=head[u];i;i=e[i].next){int v=e[i].to;if(!dfn[v]){//没访问过就递归访问tarjan(v);low[u]=min(low[u],low[v]);//获取孩子的最小的low值   }else if(ins[v]){//已经访问过且在栈中获取dfn号low[u]=min(low[u],dfn[v]);}}if(low[u]==dfn[u]){//low[u]==dfn[u]时，则从栈中不断弹出节点，直到x出栈停止。弹出的节点就是同一个连通分量的int v;	do{//一定要先执行再判断v=s.top();s.pop();be[v]=u;//把这些弹出的点标记同一个id号(连通分量号)ins[v]=0;if(u==v)break;//自己不要和自己加p[u]+=p[v];}while(v!=u);//直到是自己为止}
}int topo()
{queue <int> q;int tot=0;for (int i=1;i<=n;i++){if(be[i]==i&&!in[i]){q.push(i);dp[i]=p[i];}}while (!q.empty()){int u=q.front();q.pop();for (int i=hh[u];i;i=newe[i].next){int v=newe[i].to;dp[v]=max(dp[v],dp[u]+p[v]);//要最大的起点嘛in[v]--;if (in[v]==0) q.push(v);}}int ans=0;for (int i=1;i<=n;i++)ans=max(ans,dp[i]);return ans;
}
int main()
{scanf("%d%d",&n,&m);for (int i=1;i<=n;i++)scanf("%d",&p[i]);//权值for (int i=1;i<=m;i++){int u,v;scanf("%d%d",&u,&v);add(u,v);}for (int i=1;i<=n;i++)if (!dfn[i]) tarjan(i);for (int i=1;i<=m;i++){int u=be[e[i].from],v=be[e[i].to];//from是起点，to是终点if (u!=v)//不同的分量号点间进行建边，有重边也不影响topo结果{newe[++tt]=(node){v,hh[u],u};hh[u]=tt;in[v]++;//建新边过程，相当于add功能}}printf("%d",topo());
}