Floating Point 浮点数
文章目录
- Floating Point 浮点数
- 分数二进制示例
- 能代表的数
- 浮点数的表示方式
- 浮点数编码
- 规格化值
- 规格化值编码示例
- 非规格化的值
- 特殊值
- 示例
- IEEE 编码的一些特殊属性
- 四舍五入,相加,相乘
- 四舍五入
- 四舍五入的模式
- 二进制数的四舍五入
- 浮点数乘积
- 浮点数加法
- 浮点数的一些数学性质
- 浮点数在C中
- 类型转换的比较
- 《深入理解计算机系统》书籍学习笔记
浮点主要通过移动二进制小数点来表示尽可能大的取值范围,兼顾尽可能高的精度,同时还要受到位数有限的限制。
分数二进制示例
值 二进制表示 十进制
5 3/4 101.11 2^2 + 2^0 + 1/2^1 + 1/2^2
2 7/8 10.111 2^1 + 1/2^1 + 1/2^2 + 1/2^3
1 7/16 1.0111 2^0 + 1/2^2 + 1/2^3 + 1/2^4
- 分数除以2,就是小数点二进制右移1位。
- 乘以2, 就是小数点左移1位
- 数字0.111111111… 小于 1,无限接近于1
- 1/2 + 1/4 + 1/8 + … + 1/2^i + … -> 1.0
- 记为 1.0 - ε
能代表的数
-
只能精确地表示x/2k形式的数字
-
其他有理数有重复的位表示
值 二进制表达 十进制
1/3 0.01010101010101[01]... 1/2^2 + 1/2^4 + 1/2^6 + 1/2^8 + ...
1/5 0.001100110011[0011]... 1/2^3 + 1/2^4 + 1/2^7 + 1/2^8 + ...
1/10 0.0001100110011[0011]... 1/2^4 + 1/2^5 + 1/2^8 + 1/2^9 + ...
浮点数的表示方式
同一标准:
(–1)^s*M*2^E
看着是不是像二进制科学计数法。
- 符号位s: 决定了数是正数还是负数
- 显著值M(mantissa,小数部分): 通常是在[1.0,2.0]范围内的分数值。
- 指数E(exponent): 以2的幂表示值的权重
浮点数编码

- s 符号位
- exp 字段编码E(但是不等于E)
- frac 字段编码M (但是不等于M)
不同精度:
-
单精度:32 位(bits)
字段所占位数: s:exp:frac -> 1:8:23 -
双精度: 64 位(bits)
字段所占位数: s:exp:frac -> 1:11:52
规格化值
当exp != 000…0 , 并且exp != 111…1
指数编码有一个偏置值:E = Exp - Bias
Exp : exp字段,无符号值
Bias = 2^(k-1) -1
k 表示指数的位数
-
取值范围
单精度:k=8, Bias = 2^(8-1) - 1 = 127 (1 <= Exp <= 254, -126 <= E <= 127)
双精度: k=11,Bias = 2^(11-1) - 1 = 1023 (1 <= Exp <= 2046, -1022 <= E <= 1023) -
用隐含前导编码的有效数 1: M = 1.xxxxxx 二进制
xxxxx: 表示frac 字段编码
最小值:frac = 000…0(M=1.0)
最大值:frac = 111…1(M=2.0-ε)
注意: M 是固定前面有一个1,所以最小值才是1开始。
规格化值编码示例
-
值
Float F = 15213.0
15213 十进制 = 11101101101101 二进制
= 1.1101101101101 * 2^13 科学计数法 -
有效数
M(小数) = 1.1101101101101 二进制
frac(小数部分编码) = 1101101101101 0000000000 二进制 -
指数
E = 13
Bias = 127
Exp = 140 = 10001100 二进制 -
结果

非规格化的值
非规格化条件:exp = 000…0
指数值:E = 1 - Bias(注意:不是E = 0 - Bias)
以隐含前导0编码的有效数:M = 0.xxx…x
案例:
- exp = 000…0, frac = 000…0
代表0值 - exp = 000…0, frac != 000…0
最接近0.0的数字。
平均间隔。
特殊值
特殊值条件:exp = 111…1
案例:
-
exp = 111…1, frac = 000…0
代表无穷大。
操作溢出。
例如:正无穷大:1.0/0.0 = -1.0/-0.0 , 负无穷大:1.0/-0.0 -
exp = 111…1, frac != 000…0
Not-a-Number(NaN)
表示无法确定数值时的情况。
例如:sqrt(-1), 无穷大*0
示例
我们用简单的8位浮点数表示法,来理解浮点数。
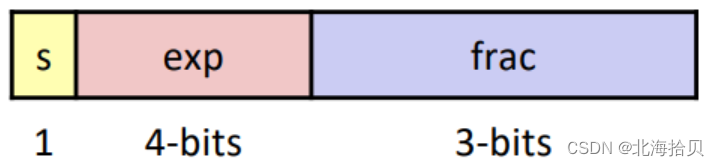
s: 1位符号位
exp: 4位指数位, 偏置位bias=2^(4-1)-1=7
frac: 3位小数位
s exp frac E Value 计算 备注
0 0000 000 -6 0 (-1)^0 * 0 * 2^(-6)
0 0000 001 -6 1/8*1/64 = 1/512 (-1)^0 * 2^(-3) * 2^(-6) // 最接近0值
0 0000 010 -6 2/8*1/64 = 2/512 (-1)^0 * 2^(-2) * 2^(-6)
…
0 0000 110 -6 6/8*1/64 = 6/512 (-1)^0 * 2^(-1)*2^(-2) * 2^(-6)
0 0000 111 -6 7/8*1/64 = 7/512 (-1)^0 * 2^(-1)*2^(-2)* 2^(-3) * 2^(-6) // 最大的非规格化值
0 0001 000 -6 8/8*1/64 = 8/512 (-1)^0 * 1 * 2^(-6) // 最小的规格化值
0 0001 001 -6 9/8*1/64 = 9/512 (-1)^0 * (1 + 2^(-3)) * 2^(-6)
…
0 0110 110 -1 14/8*1/2 = 14/16 (-1)^0 * (1 + 2^(-1)*2^(-2)) * 2^(-1)
0 0110 111 -1 15/8*1/2 = 15/16 (-1)^0 * (1 + 2^(-1)*2^(-2)* 2^(-3)) * 2^(-1) // 最接近1的(小于1的数)
0 0111 000 0 8/8*1 = 1 (-1)^0 * 1 * 2^0
0 0111 001 0 9/8*1 = 9/8 (-1)^0 * (1 + 2^(-3)) * 2^0 // 最接近1的(大于1的数)
0 0111 010 0 10/8*1 = 10/8 (-1)^0 * (1 + 2^(-2)) * 2^0
…
0 1110 110 7 14/8*128 = 224 (-1)^0 * (1 + 2^(-1)*2^(-2)) * 2^7
0 1110 111 7 15/8*128 = 240 (-1)^0 * (1 + 2^(-1)*2^(-2)* 2^(-3)) * 2^7 // 最大的规格化数
0 1111 000 7 inf
值的计算公式:v = (–1)^s * M * 2^E
规格化数: E = Exp – Bias
非规格化数: E = 1 – Bias
IEEE 编码的一些特殊属性
-
浮点数(FP)的0值和整型0值一样
所有的位都是0 -
除了非数字(NaN)之外,你可以比较任何浮点数。
当作无符号数来比较。
四舍五入,相加,相乘
四舍五入
基本思想:
- 先计算得到一个准确的值
- 然后根据你期望的精度进行处理
- 如果指数太大的化,可能会溢出
- 可能需要四舍五入来满足小数位数(frac)
四舍五入的模式
$1.40 $1.60 $1.50 $2.50 –$1.50
向0舍入 $1 $1 $1 $2 –$1
向下舍入 $1 $1 $1 $2 –$2
向上舍入 $2 $2 $2 $3 –$1
向偶数舍入 $1 $2 $2 $2 –$2
向0舍入:向0的方向舍去小数。
向下舍入:类似向下取整
向上舍入:类似向上取整
向偶数舍入:在四舍五入的基础上,考虑向偶数靠近,主要是在中位数时的处理方式和四舍五入不同。
二进制数的四舍五入
奇数是1,0是偶数。
二进制中间数100…,十进制中间数是500…
精度时小数后两位:
Value Binary Rounded Action Rounded Value
2 3/32 10.000112 10.002 (<1/2—down) 2
2 3/16 10.001102 10.012 (>1/2—up) 2 1/4
2 7/8 10.111002 11.002 ( 1/2—up) 3
2 5/8 10.101002 10.102 ( 1/2—down) 2 1/2
浮点数乘积
相乘:((–1)^s1 * M1 * 2^E1) x ((–1)^s2 * M2 * 2^E2)
准确值:: (–1)^s * M * 2^E
符号位 s: s1 ^ s2
有效位 M: M1 x M2
指数位 E: E1 + E2
修正:
- 如果 M >= 2, M 右移,增加E
- 如果E 超出范围,溢出
- 四舍五入 M 来符合精度要求。
浮点数加法
相加:((–1)^s1 * M1 * 2^E1) + ((–1)^s2 * M2 * 2^E2)
假设:E1 > E2
准确值:: (–1)^s * M * 2^E
符号位 s, 有效位 M: 对齐相加
指数位E: E1
修正:
- 如果 M >= 2, 右移M, 增加E。(小数点右移)
- 如果 M < 1, 左移 M 的 k 个位置, 减少 E 的 k。(小数点左移)
- 如果E超出范围溢出
- 将 M 适应小数(frac)精度
浮点数的一些数学性质
浮点数加法的数学性质:
- 与阿贝尔群的比较
- 加法封闭: 满足
- 但是可能产生 无穷大和NaN
- 结合律:满足
- 交换律:不满足
- 进行四舍五入时,可能溢出和不精确
- (3.14+1e10)-1e10 = 0, 3.14+(1e10-1e10) = 3.14
- 每个元素都有可加逆:几乎满足
- 除了无穷大和NaN
- 加法封闭: 满足
- 单调性
- a ≥ b ⇒ a+c ≥ b+c : 几乎满足
- 除了无穷大和NaN
- a ≥ b ⇒ a+c ≥ b+c : 几乎满足
浮点数乘法的数学性质和加法是类似的。
浮点数在C中
无符号和有符号的转换,从未改变过位的表示(位上的实际值),只是改变了某些位的解释方式。
整数,单精度浮点数,双进度浮点数的转换,位的表示发生了变化(实际值改变了),会对位的值产生实际影响。
- double/float -> int
- 截取小数部分
- 就像向0舍入
- int -> double
精确的转换,只要int(32) <= 53 位大小。 - int -> float
将会进行四舍五入操作。
类型转换的比较
三个不同类型的变量:
int x = …;
float f = …;
double d = …;
一些特性的比较:
* x == (int)(float) x // false
• x == (int)(double) x // true
• f == (float)(double) f // true
• d == (double)(float) d // false
• f == -(-f); // true
• 2/3 == 2/3.0 // false. 2/3=0 整数, 2/3.0 是浮点数。
• d < 0.0 ⇒ ((d*2) < 0.0) // true, 浮点数即使溢出也是负无穷大数
• d > f ⇒ -f > -d // true, 单调性
• d * d >= 0.0 // true
• (d+f)-d == f // false, 不满足结合律
《深入理解计算机系统》书籍学习笔记
《深入理解计算机系统》学习笔记 - 第一课 - 课程简介
《深入理解计算机系统》学习笔记 - 第二课 - 位,字节和整型
《深入理解计算机系统》学习笔记 - 第三课 - 位,字节和整型
《深入理解计算机系统》学习笔记 - 第四课 - 浮点数
《深入理解计算机系统》学习笔记 - 第四课 - 机器级别的程序

![[VSCode] Java开发环境配置](https://img-blog.csdnimg.cn/direct/a606654342694f43b7505ebf39c9eca5.png#pic_center)