概述
DDD领域驱动设计是架构方法论,适用于业务逻辑较复杂系统。
DDD核心目的能输出领域如何划分,以及架构分层如何构建。
本文章系列会分2部分讲述DDD:1、DDD原理;2、DDD实践。DDD原理分为战略及战术设计2篇来讲述;
架构的本质上就是通过定义不同组件及组件间的关系实现高扩展性,可维护性,控制复杂度(手段);最终通过架构来实现高效迭代(目的);比如一个支付渠道的接入是否能影响最小的组件来实现扩展。
而DDD通过战略设计来划分出业务域以及定义不同域间的关系;这样相同域的业务需求能在一个业务域完成而不会影响到其它域,无论从开发&测试&部署维度都能影响最小。
DDD通过战述设计来找出实体,聚合,聚合根,以及确定架构分层:Clean架构,CQRS等。
原理篇整体以战略设计及战术设计做为2大章节来叙述。
战略设计
目的
产出领域模型,领域的划分,定义核心域,通用域,支撑域。最终实现:控制业务架构复杂度,提供高扩展&可维护性,从而提升业务迭代效率。
概念
领域:企业要做事情集合。包含了业务流程,角色。如结算域就是一个领域,结算域涉及很多业务流程:如运营设置费用项,商家入驻生成结算合同,交易确认收货进行结算给平台及结算给商户。
子域:领域的细分。细分的目的是为了控制复杂度。如结算又可根据结算阶段分为收单,计费等子域。
核心域:企业核心能力,需要投入重点资源来跟进;比如电商中交易,供应链,支付。
通用域如用户权限域,通用域可供不同业务使用。
支撑域:电商中的服务,在垂直电商刚起步时,服务可以做为支撑域采用采购形式让业务整体能run起来。后续根据业务发展,服务变成关键要素,此时服务再提升为核心域投入重点资源进入升级。
限界上下文:是业务的边界。包含若干领域或子域。在业务边界内同一个实体拥有同一个语义。原则上限界上下文必须包含完整的业务流程。如结算中的计费子域对应一个限界上下文,其中包含了运营设置计费项以及后续确认收货后计费业务流程。
怎么划分
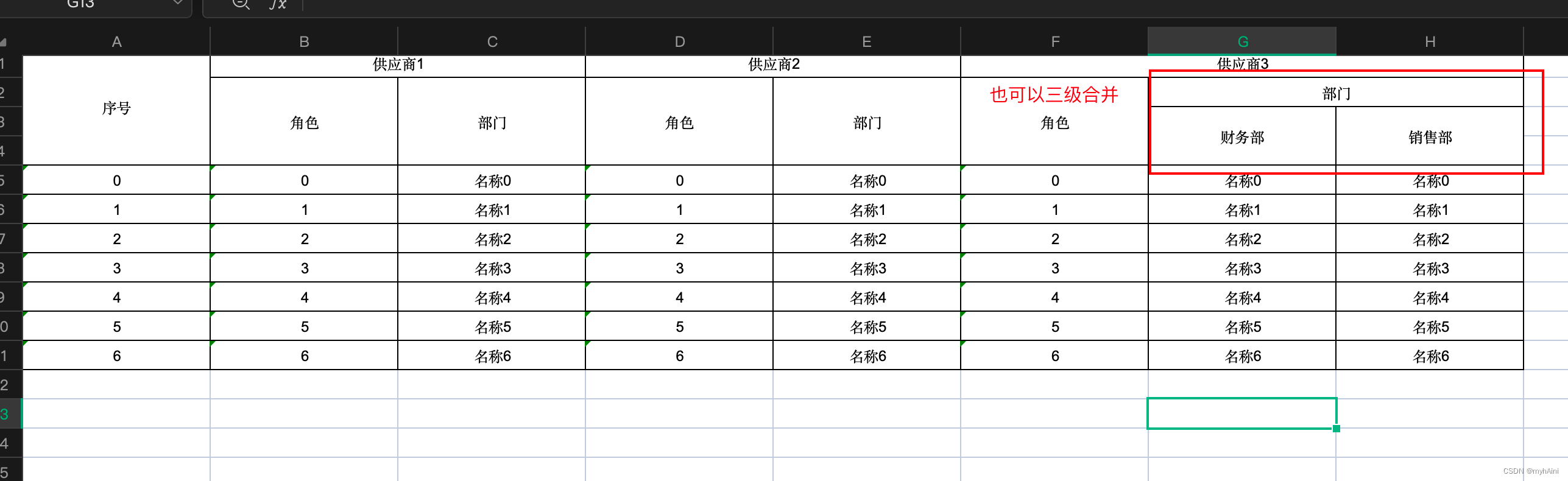
1、领域模型确定
通常使用事件风暴来进行,如结算业务中,事件风暴如下。

2、限界上下文划分
根据领域模型业务职责分类及相关性,最终能形成计费,清算,结算,合同限界上下文;
费用项&计费单合到计费限界上下文。why?本质上费用项及计费单都是做的计费的业务事情。费用项是计费的基础。反过来如果费用项拆到其它限界上下文会发现计费的这个需求会涉及到2个域,增加了协同成本。
由于商家与财务视角看到的计费项不同,所以以商家视角单拆出清算限界上下文。
结算单对应到结算限界上下文中,这中间的语义有结算单:核心定义给商家在什么时候结算多少钱。打款单对应到打款限界上下文,对应一笔实际与出资渠道对应的一条打款流水单。

3、由限界上下文再合并成子域
计费上下文形成计费子域。合同上下文则形成结算合同子域。清算限界上下文形成清算子域。
结算及打款合成一个结算子域:结算单与打款单需要高频协同因此从团队协作上及代码维扩展上放在一个子域。




![[LeetCode]-283. 移动零-1089. 复写零](https://img-blog.csdnimg.cn/direct/d8b6a4cde98b4cfc9f59b55a0bb96dd8.gif)