一、初值问题简述

        在多变量微积分中，初值问题是一个常微分方程以及一个初始条件，该初始条件指定域中给定点处未知函数的值。在物理学或其他科学中对系统进行建模通常相当于解决初始值问题。

        通常给定的微分方程有无数个解，因此我们很自然地会问我们要使用哪一个。要选择一种解决方案，需要更多信息。一些有用的特定信息是初始值，它是用于查找特定解决方案的有序对。

具有一个或多个初始值的微分方程称为初值问题。

        一般规则是初值问题所需的初值数量等于微分方程的阶数。例如，如果我们有微分方程， 然后是一个初始值，当这些方程放在一起时，就形成了一个初始值问题。

        微分方程是二阶的，所以我们需要两个初始值。对于阶数大于1的初始值问题，自变量应使用相同的值。该二阶方程的初始值的一个示例是y和。这两个初值与微分方程一起构成初值问题。

        这些问题之所以如此命名，是因为未知函数中的自变量通常是，代表时间。因此，值为代表问题的开始。

二、示例1

        验证该功能是初值问题的一个解。

        对于满足初值问题的函数，它必须同时满足微分方程和初始条件。为了表明满足微分方程，我们首先计算。

        这给出了，接下来我们将两者替换和代入微分方程左侧并化简：

        这等于微分方程的右侧，所以使用。

        接下来我们计算。

        该结果验证了初始值。因此给定函数满足初值问题。

三、小结

        在前面的示例中，初始值问题由两部分组成。第一部分是微分方程，第二部分是初始值。这两个方程共同构成了初值问题。

        一般来说也是如此。初值问题由两部分组成：微分方程和初始条件。

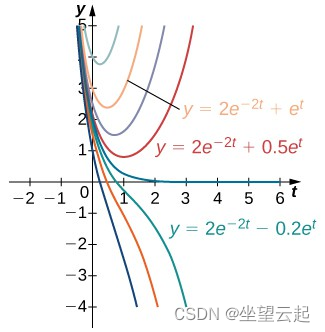
        微分方程有一系列解，初始条件决定了。示例中微分方程的解族由下式给出。该解决方案系列如图 2 所示，其中对特定解决方案进行了标记。

四、测试

        对于c的任何值，函数，是方程的解，求c的值，对于该值，解满足初始条件。

链接：https://pan.baidu.com/s/1bR9c2I0pJzWKs9DxvXMQ6Q?pwd=ssl9 
提取码：ssl9

134898100.png