题目

标题和出处

标题：在受污染的二叉树中查找元素

出处：1261. 在受污染的二叉树中查找元素

难度

5 级

题目描述

要求

给出一个满足下述规则的二叉树：

1. $\text{root.val}=\text{0}$
2. 如果 $\text{treeNode.val}=\text{x}$ 且 $\text{treeNode.left}\ne \text{null}$，那么 $\text{treeNode.left.val}=\text{2}\times \text{x}+\text{1}$
3. 如果 $\text{treeNode.val}=\text{x}$ 且 $\text{treeNode.right}\ne \text{null}$，那么 $\text{treeNode.right.val}=\text{2}\times \text{x}+\text{2}$

现在这个二叉树受到污染，所有的 $\text{treeNode.val}$ 都变成了 $\text{-1}$。

实现 $\text{FindElements}$ 类：

• $\text{FindElements(TreeNode* root)}$ 用受污染的二叉树初始化对象，并将二叉树还原。
• $\text{bool find(int target)}$ 判断目标值 $\text{target}$ 是否存在于还原后的二叉树中，如果存在则返回 $\text{true}$。

示例

示例 1：

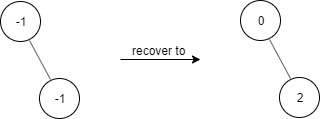
输入：
$\text{["FindElements","find","find"]}$
$\text{[[[-1,null,-1]],[1],[2]]}$
输出：
$\text{[null,false,true]}$
解释：
$\text{FindElements findElements = new FindElements([-1,null,-1]);}$
$\text{findElements.find(1);}$ // 返回 $\text{False}$
$\text{findElements.find(2);}$ // 返回 $\text{True}$

示例 2：

输入：
$\text{["FindElements","find","find","find"]}$
$\text{[[[-1,-1,-1,-1,-1]],[1],[3],[5]]}$
输出：
$\text{[null,true,true,false]}$
解释：
$\text{FindElements findElements = new FindElements([-1,-1,-1,-1,-1]);}$
$\text{findElements.find(1);}$ // 返回 $\text{True}$
$\text{findElements.find(3);}$ // 返回 $\text{True}$
$\text{findElements.find(5);}$ // 返回 $\text{False}$

示例 3：

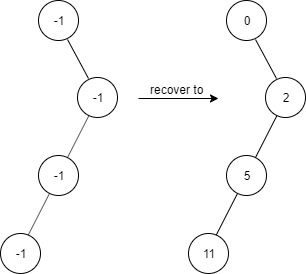
输入：
$\text{["FindElements","find","find","find","find"]}$
$\text{[[[-1,null,-1,-1,null,-1]],[2],[3],[4],[5]]}$
输出：
$\text{[null,true,false,false,true]}$
解释：
$\text{FindElements findElements = new FindElements([-1,null,-1,-1,null,-1]);}$
$\text{findElements.find(2);}$ // 返回 $\text{True}$
$\text{findElements.find(3);}$ // 返回 $\text{False}$
$\text{findElements.find(4);}$ // 返回 $\text{False}$
$\text{findElements.find(5);}$ // 返回 $\text{True}$

数据范围

• $\text{TreeNode.val}=\text{-1}$
• 二叉树的高度不超过 $\text{20}$
• 树中结点数目在范围 ${\text{[1, 10}}^{\text{4}}\text{]}$ 内
• 调用 $\text{find()}$ 的总次数在范围 ${\text{[1, 10}}^{\text{4}}\text{]}$ 内
• $\text{0}\le \text{target}\le {\text{10}}^{\text{6}}$

前言

这道题给定受污染的二叉树，要求还原二叉树然后判断每个元素是否在还原后的二叉树中。

还原二叉树可以通过遍历二叉树实现。根结点值还原成 $0$，对于每个已经还原的结点，如果结点值是 $x$，则当其左子结点不为空时将左子结点值设为 $2\times x+1$，当其右子结点不为空时将右子结点值设为 $2\times x+2$。

还原二叉树之后，查找元素的最直观做法是假设还原后的二叉树中存在目标值结点，找到从根结点到目标值结点的路径。为了找到路径，从目标值结点开始每次寻找当前结点的父结点，直到定位到父结点。找到路径之后，从父结点出发向目标值结点移动，判断路径上的结点是否都存在，如果都存在则目标值在还原后的二叉树中，否则目标值不在还原后的二叉树中。

使用上述做法查找元素，每次查找的时间复杂度和二叉树的高度有关。时间复杂度更低的做法是用哈希集合存储结点值，在构造方法中遍历并还原二叉树，同时将还原后的二叉树中的每个结点值存入哈希集合中，在查找元素时只需要判断目标值是否在哈希集合中即可。

解法一

思路和算法

可以使用深度优先搜索遍历并还原二叉树。

构造方法中，将根结点值设为 $0$，从根结点开始遍历，遍历操作如下。

1. 用 $\text{value}$ 表示当前结点值，将 $\text{value}$ 加入哈希集合。

2. 如果当前结点的左子结点不为空，则将左子结点值设为 $2\times \text{value}+1$，然后遍历左子树。

3. 如果当前结点的右子结点不为空，则将右子结点值设为 $2\times \text{value}+2$，然后遍历右子树。

查找元素时，判断目标值是否在哈希集合中。

代码

class FindElements {Set<Integer> values;public FindElements(TreeNode root) {values = new HashSet<Integer>();root.val = 0;dfs(root);}public boolean find(int target) {return values.contains(target);}private void dfs(TreeNode node) {int value = node.val;values.add(value);TreeNode left = node.left, right = node.right;if (left != null) {left.val = 2 * value + 1;dfs(left);}if (right != null) {right.val = 2 * value + 2;dfs(right);}}
}

复杂度分析

• 时间复杂度：构造方法的时间复杂度是 $O(n)$，查找操作的时间复杂度是 $O(1)$，其中 $n$ 是二叉树的结点数。构造方法需要遍历每个结点一次并将每个结点值加入哈希集合，需要 $O(n)$ 的时间。查找操作判断目标值是否在哈希集合中，需要 $O(1)$ 的时间。

• 空间复杂度：$O(n)$，其中 $n$ 是二叉树的结点数。需要使用哈希集合存储还原后的二叉树中的每个结点值。

解法二

思路和算法

也可以使用广度优先搜索遍历并还原二叉树。

构造方法中，将根结点值设为 $0$，然后从根结点开始遍历。使用队列存储待访问的结点，初始时将根结点入队列。每次将一个结点出队列，执行如下操作，直到队列为空时遍历结束。

1. 用 $\text{value}$ 表示当前结点值，将 $\text{value}$ 加入哈希集合。

2. 如果当前结点的左子结点不为空，则将左子结点值设为 $2\times \text{value}+1$，然后将左子结点入队列。

3. 如果当前结点的右子结点不为空，则将右子结点值设为 $2\times \text{value}+2$，然后将右子结点入队列。

查找元素时，判断目标值是否在哈希集合中。

代码

class FindElements {Set<Integer> values;public FindElements(TreeNode root) {values = new HashSet<Integer>();root.val = 0;Queue<TreeNode> queue = new ArrayDeque<TreeNode>();queue.offer(root);while (!queue.isEmpty()) {TreeNode node = queue.poll();int value = node.val;values.add(value);TreeNode left = node.left, right = node.right;if (left != null) {left.val = 2 * value + 1;queue.offer(left);}if (right != null) {right.val = 2 * value + 2;queue.offer(right);}}}public boolean find(int target) {return values.contains(target);}
}

复杂度分析

• 时间复杂度：构造方法的时间复杂度是 $O(n)$，查找操作的时间复杂度是 $O(1)$，其中 $n$ 是二叉树的结点数。构造方法需要遍历每个结点一次并将每个结点值加入哈希集合，需要 $O(n)$ 的时间。查找操作判断目标值是否在哈希集合中，需要 $O(1)$ 的时间。

• 空间复杂度：$O(n)$，其中 $n$ 是二叉树的结点数。需要使用哈希集合存储还原后的二叉树中的每个结点值。