介绍
在前面课程我们讲过使用 DBCA 创建数据库以及搭建 DataGuard 等功能,在多租户这章节,要讲下如何使用 DBCA 克隆 PDB。
- 18C 开始支持使用 DBCA 在本地 CDB 中克隆 PDB
- 19C 升级支持使用 DBCA 克隆 PDB 到远端 CDB 中
- 19C 升级支持使用 DBCA 重定向迁移 PDB 到远端 CDB 中
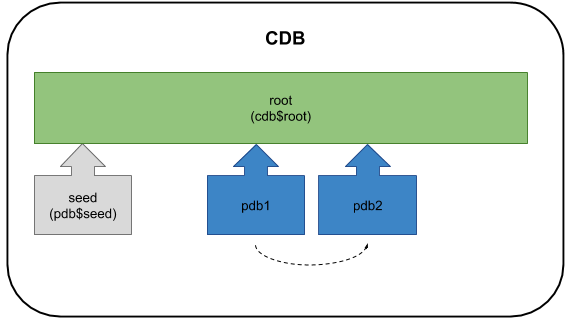
本地克隆
在 18C 中,我们可以使用 dbca -createPluggableDatabase -createPDBFrom PDB 命令在本地 CDB 中克隆 PDB,本地克隆的方式比较简单,但是感觉实用性不大。
创建语法如下:
[-createPDBFrom {DEFAULT | FILEARCHIVE | RMANBACKUP | USINGXML | PDB}[-pdbArchive