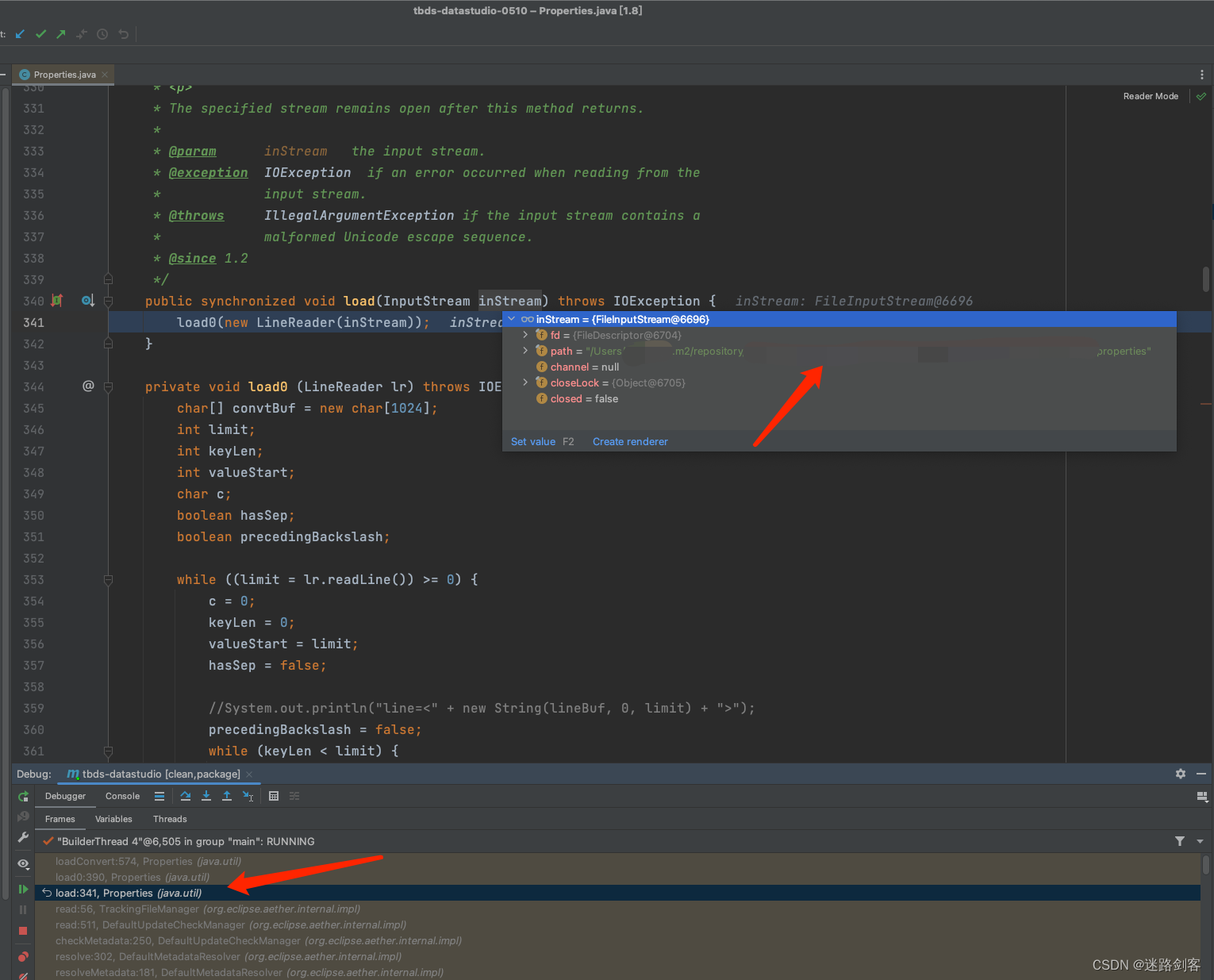
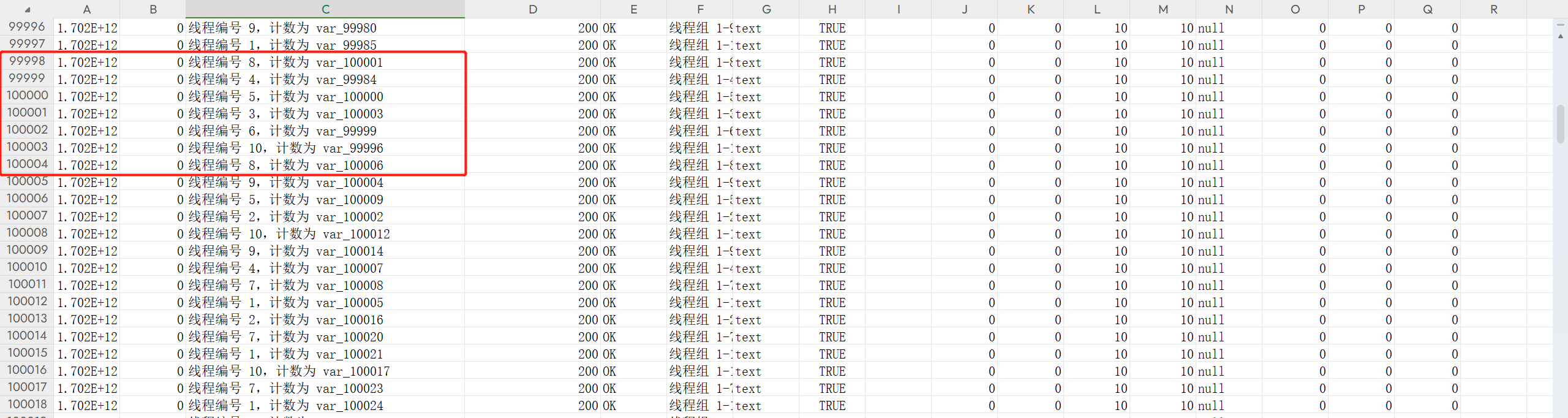
Idea maven打包时 报错 illegalArgumentException: Malformed \uxxxx encoding 解决方法
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.rhkb.cn/news/215948.html
如若内容造成侵权/违法违规/事实不符,请联系长河编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
DNSLog漏洞探测(三)之XSS漏洞实战
DNSLog漏洞探测(三)之XSS漏洞实战
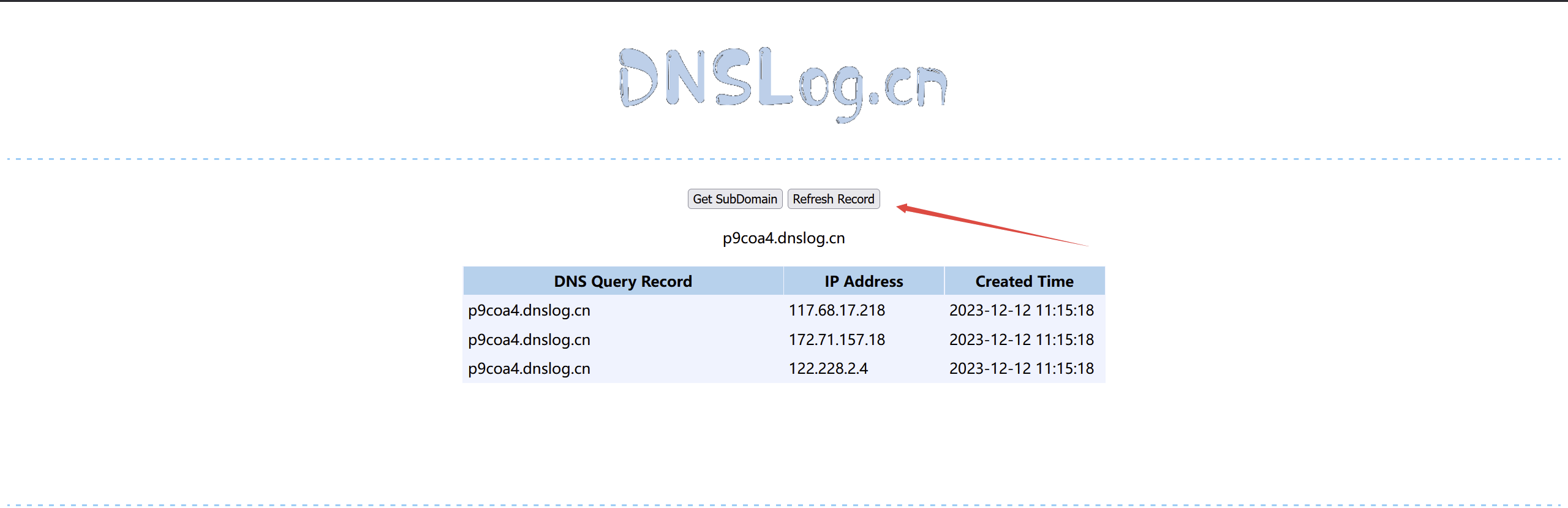
通过前面的学习,我们已经明白了什么是DNSLog平台,那么DNSLog平台到底能为我们做些什么呢?
DNSLog的平台实际使用很长见的一种情况就是针对漏洞无回显的情况,我们通过让受害者的服务器主动发起对…
Navicat 技术指引 | 适用于 GaussDB 分布式的数据迁移工具
Navicat Premium(16.3.3 Windows 版或以上)正式支持 GaussDB 分布式数据库。GaussDB 分布式模式更适合对系统可用性和数据处理能力要求较高的场景。Navicat 工具不仅提供可视化数据查看和编辑功能,还提供强大的高阶功能(如模型、结…
【性能测试】Jmeter 配置元件(一):计数器
Jmeter 配置元件(一):计数器 在 Jmeter 中,通过函数 ${__counter(,)} 可以实现每次加 1 1 1 的计数效果。但如果步长不为 1 1 1,则要利用到我们的计数器。
函数作用${__counter(,)}计数器,每次加 1${__d…
【自定义Source、Sink】Flink自定义Source、Sink对redis进行读写操作
使用ParameterTool读取配置文件
Flink读取参数的对象
Commons-cli: Apache提供的,需要引入依赖ParameterTool:Flink内置 ParameterTool 比 Commons-cli 使用上简便; ParameterTool能避免Jar包的依赖冲突 建议使用第二种 使用Par…
概率论之 证明 正态分布的上a 分位点的对称的性质
公式(Z(a) -Z(1-a)) 表示正态分布的上(a)分位点与下(1-a)分位点在分布曲线上关于均值的对称性。 左侧 (Z(a)): 这是分布曲线上累积概率为(a)的那个点。也就是说,这是一个使得这个点及其左侧的面积占据整个曲线下方(a)的位置。 右侧 (Z(1-a))࿱…
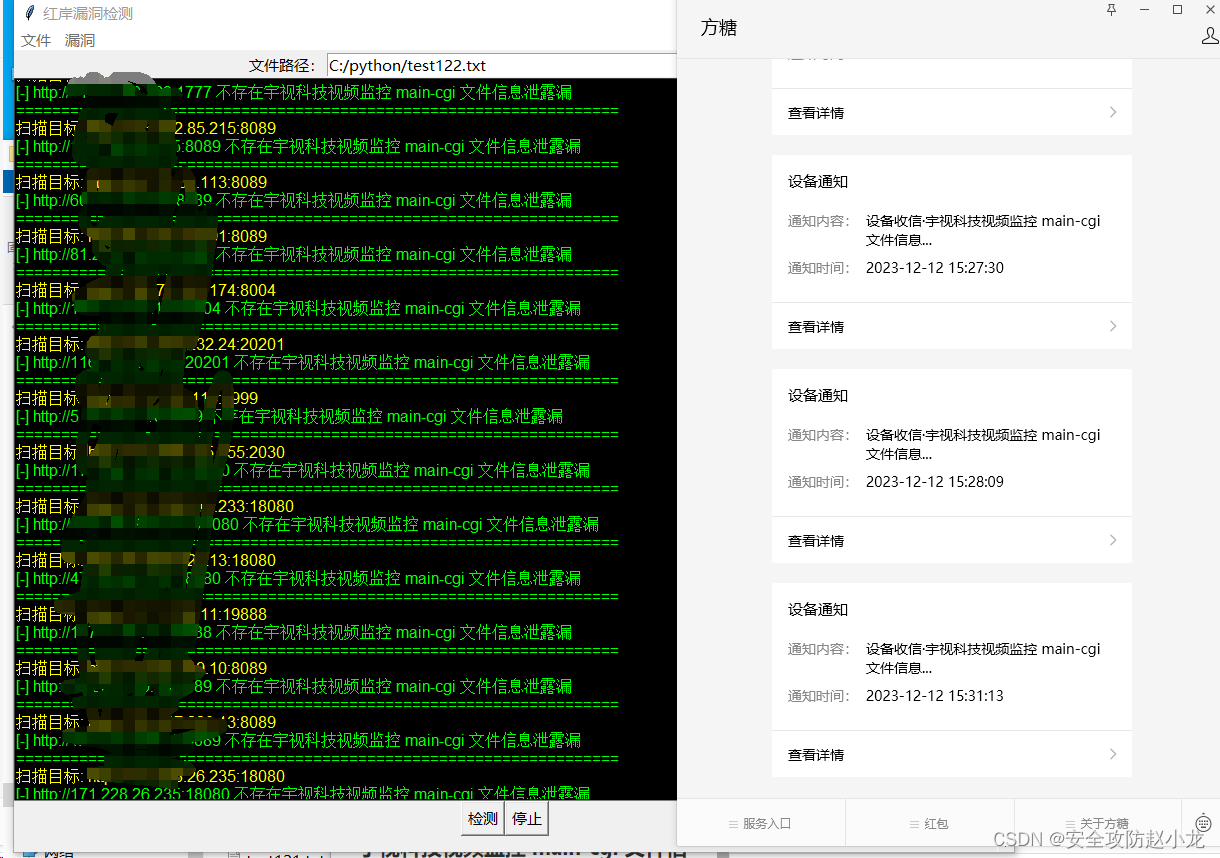
宇视科技视频监控 main-cgi 文件信息泄露漏洞
宇视科技视频监控 main-cgi 文件信息泄露漏洞 一、产品简介二、漏概述三、复现环境四、漏洞检测手工抓包自动化检测 免责声明:请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工具而造成的任何直接或者间接的后果及损失&#…
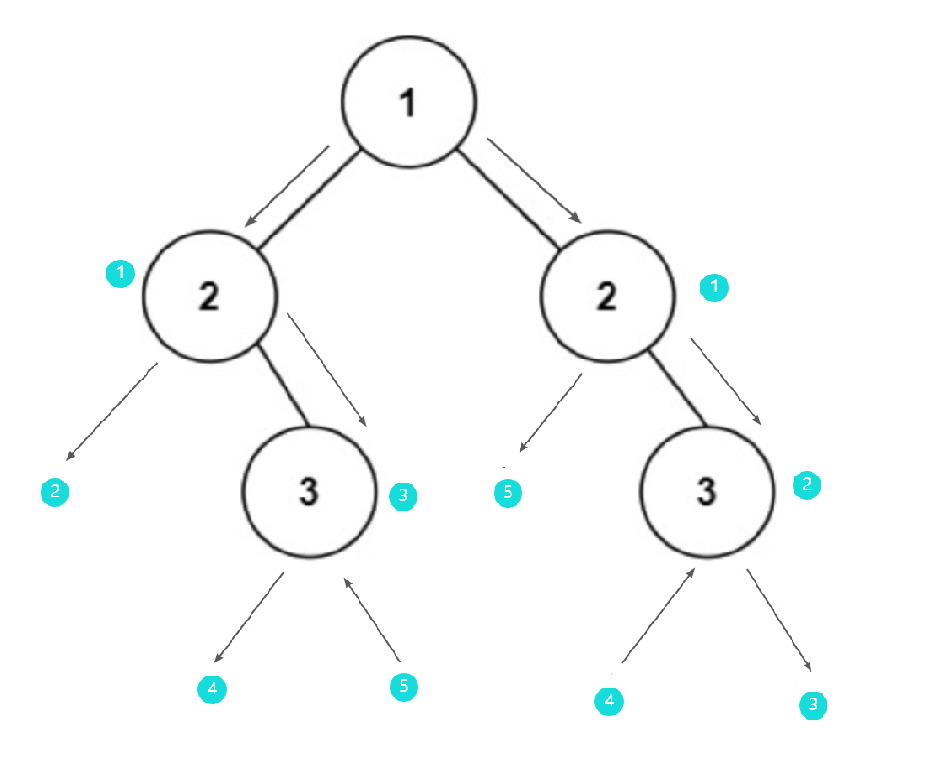
leetcode 101.对称二叉树
学习这部分还是要多画图,多思考 101.对称二叉树 题目 给你一个二叉树的根节点 root , 检查它是否轴对称。 题目链接 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 文字 和 画图 分析 明确结束条件和继续递归条件 判断是否对称…
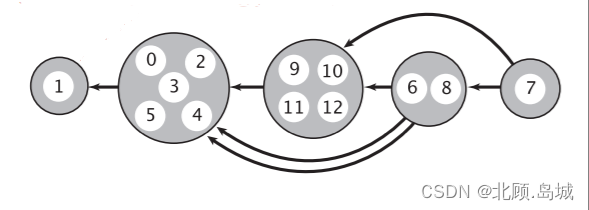
【LeetCode题目拓展】第207题 课程表 拓展(拓扑排序、Tarjan算法、Kosaraju算法)
文章目录 一、拓扑排序题目二、题目拓展1. 思路分析2. tarjan算法3. kosaraju算法 一、拓扑排序题目
最近在看一个算法课程的时候看到了一个比较好玩的题目的扩展,它的原题如下: 对应的LeetCode题目为 207. 课程表
这个题目本身来说比较简单ÿ…
Linux——基本指令(二)
个人主页:日刷百题
系列专栏:〖C语言小游戏〗〖Linux〗〖数据结构〗 〖C语言〗
🌎欢迎各位→点赞👍收藏⭐️留言📝
写在前面:
紧接上一章,我们在理解接下来的命令之前,…
nodejs微信小程序+python+PHP的外卖数据分析-计算机毕业设计推荐django
目 录 摘 要 I ABSTRACT II 目 录 II 第1章 绪论 1 1.1背景及意义 1 1.2 国内外研究概况 1 1.3 研究的内容 1 第2章 相关技术 3 2.1 nodejs简介 4 2.2 express框架介绍 6 2.4 MySQL数据库 4 第3章 系统分析 5 3.1 需求分析 5 3.2 系统可行性分析 5 3.2.1技术可行性:…
Appium 自动化自学篇 —— 初识Appium自动化!
Appium 简介
随着移动终端的普及,手机应用越来越多,也越来越重要。而作为测试 的我们也要与时俱进,努力学习手机 App 的相关测试,文章将介绍手机自动化测试框架 Appium 。 那究竟什么是 Appium 呢? 接下来我们一起来学习PythonS…
鸿蒙开发之状态管理@State
1、视图数据双向绑定
鸿蒙开发采用的声明式UI,利用状态驱动UI的更新。其中State被称作装饰器,是一种状态管理的方式。
状态:指的是被装饰器装饰的驱动视图更新的数据。
视图:是指用户看到的UI渲染出来的界面。
之所以成为双向…
基于Python+WaveNet+MFCC+Tensorflow智能方言分类—深度学习算法应用(含全部工程源码)(四)
目录 前言引言总体设计系统整体结构图系统流程图 运行环境模块实现1. 数据预处理2. 模型构建3. 模型训练及保存4. 模型生成 系统测试1. 训练准确率2. 测试效果 相关其它博客工程源代码下载其它资料下载 前言
博主前段时间发布了一篇有关方言识别和分类模型训练的博客ÿ…
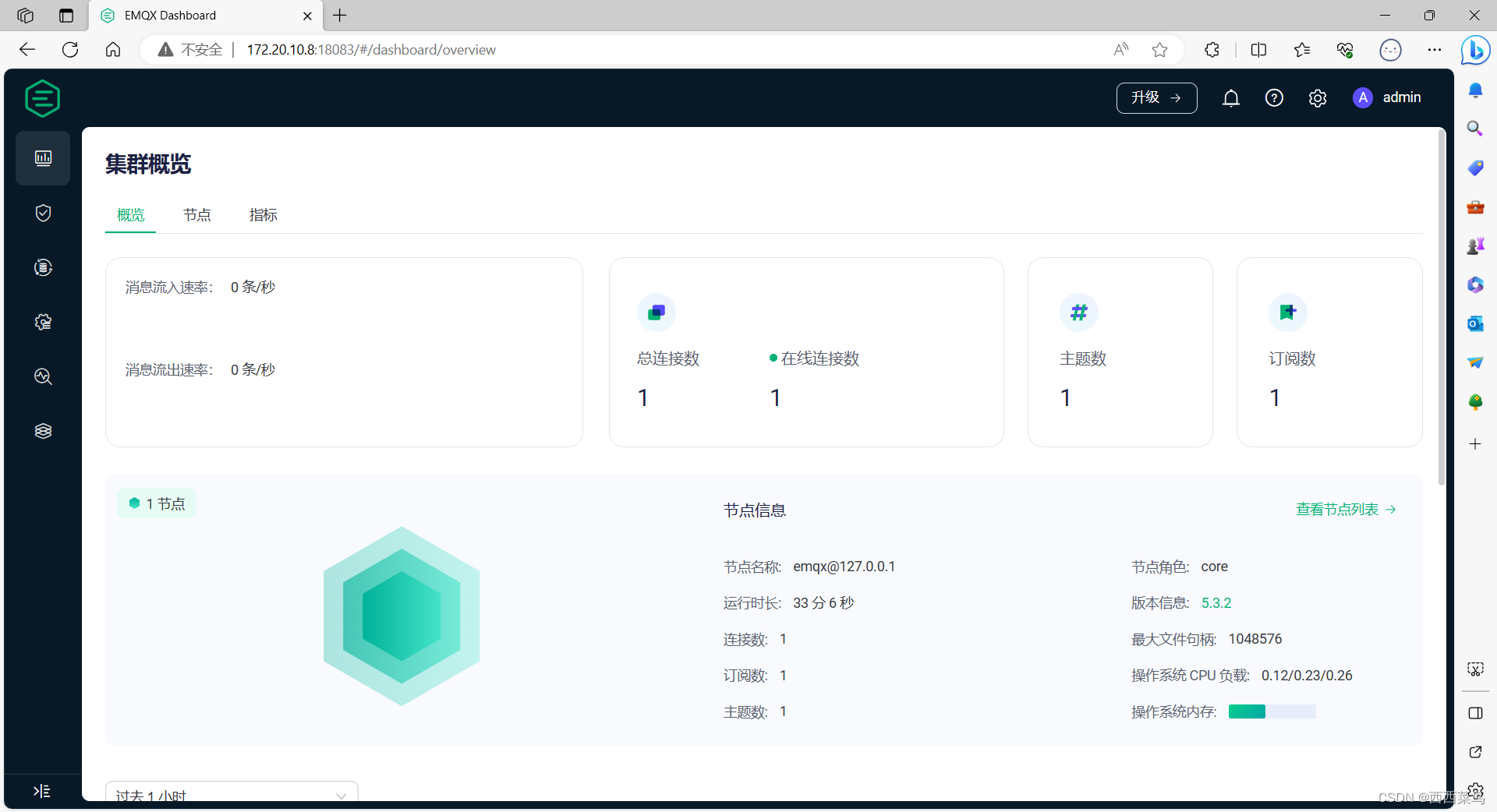
Ubuntu部署EMQX开源版MQTT服务器-Orange Pi部署-服务器部署
一、前言 作为全球最具扩展性的 MQTT 消息服务器,EMQX 提供了高效可靠海量物联网设备连接,能够高性能实时移动与处理消息和事件流数据,本文将介绍如何在Ubuntu 22.04上部署MQTT服务器。我们本次选择开源版,使用离线安装方式部署。…
【Amis Low Code 结合FastAPI进行前端框架开发】
官方文档
封装思想
直接复制官网json数据即可开发每个json中的接口由fastapi 转发(透传)使其开发模式与前端思维一致
基础组件
from amis import Page, Service, App
from pydantic import BaseModel, Field
from fastapi import FastAPI, Request, …
智能优化算法应用:基于鸡群算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于鸡群算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于鸡群算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.鸡群算法4.实验参数设定5.算法结果6.参考文献7.MA…
MySQL进阶(MySQL学习笔记)
接上回MySQL基础篇
数据完整性约束
定义完整性约束
实体完整性
主键约束
(1)作为列的完整性约束 (2)作为表的完整性约束 2.候选键约束
将id字段和user字段设置为候选键 参照完整性
将classid字段设置为外键 用户定义完整性…