数据结构之归并排序及排序总结

归并排序

归并排序的时间复杂度

排序的稳定性

排序总结

归并排序

归并排序大家只需要掌握其递归方法即可，非递归方法由于在某些特殊场景下边界难控制，我们一般很少使用非递归实现归并排序。那么归并排序的递归方法我们究竟是怎样实现呢？

大家先想象一下这样一种场景，如果现在有两个数，我们要将这两个数排成升序，怎样呢？很简单，我们只需要将两个数进行一次大小的比较即可，比较完之后，小的元素放在前面，大的元素放在后面，其实这就是很简单的一次归并排序，两个素比较之后交换使得两个元素变得有序的场景我们就称作一次归并。

我们再次深入分析，如果有两个元素，这两个元素可以直接比较，且比较之后两个数就变得有序，以此类推，如果们要对4个元素进行归并排序，按照此逻辑，将两两分成一组，然后这两组进行一次比较，比较完成之后，这4个元素应该就变有序了，但是事实真是这样吗？通过示意图为大家讲解：

为什么两个元素互相比较就可以变得有序呢？

这是因为当一个数组中只有一个数时，我们就可以称这个数组是有序的，当数组中有两个元素时，我们可以将这两个数每一个数都看成一个数组，此时这两个数组都是有序的，两个有序的数组，元素之间依次比较，肯定会将最终的整个数组变得有序，所以，我们要使四个数组变得有序，可以将数组分成左右两个数组，当我们使左右两个数组有序时，再将左右两个数组的元素依次进行比较，这样，最终四个数组成的数组就会有序。以此，归并排序的递归思路就出来了：

通过四个元素的数组为大家图示讲解归并排序的思想：

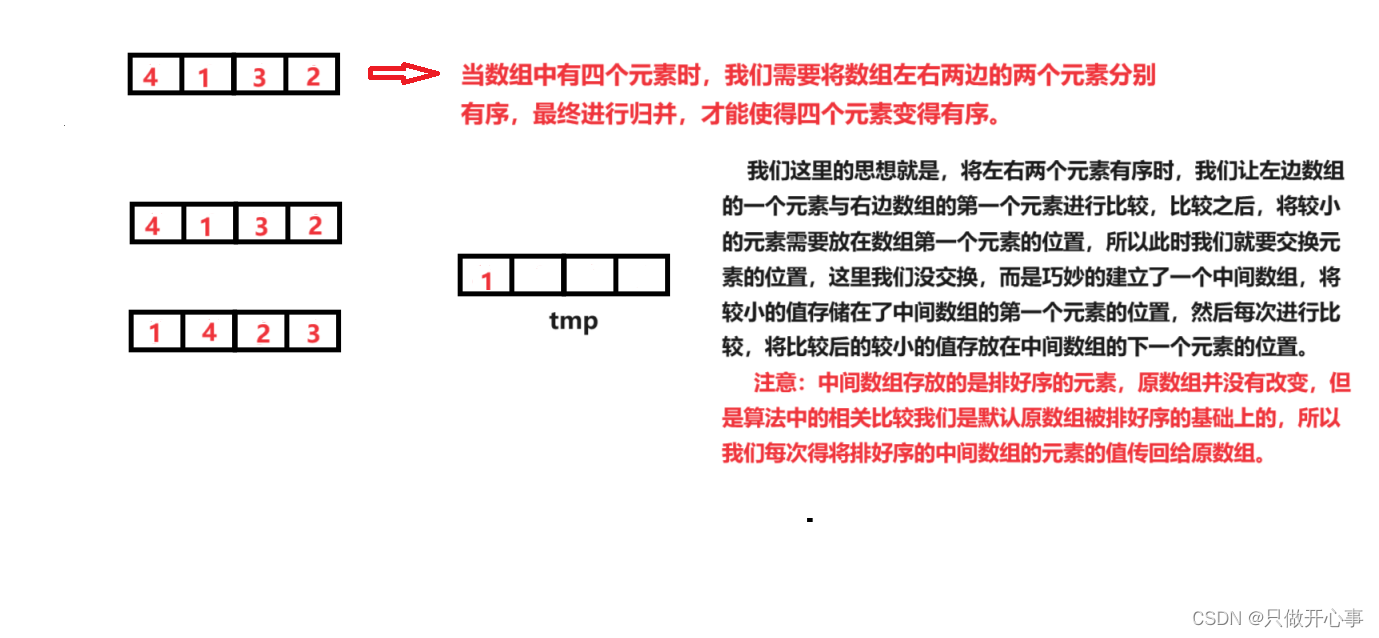
归并排序的思想：我们要对一个数组进行归并排序，使它变得有序，我们就得先将这个数组分成左右两部分，相对左边这部分数组进行归并排序，然后再对右边这部分数组进行归并排序，左右两边的数组排好序之后，对左右两个数组的元素进行一次比较，我们也成对左右两个数组的元素进行归并，然后整个数组的归并排序就完成了。

归并排序的整体代码：

void _MergeSort(int* a, int left, int right, int* tmp)
{if (left >= right)return;int mid = (right + left) / 2;_MergeSort(a, left, mid, tmp);_MergeSort(a, mid + 1, right, tmp);int begin1 = left, begin2 = mid + 1;int end1 = mid, end2 = right;int i = left;//左右数组有序之后，就需要左右数组进行归并while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}//左右两个数组，当一个数组归并完时，一个数组可能还没有归并完，将没有归并完的这个数组的元素依次赋值给中间数组while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin1 <= end1){tmp[i++] = a[begin2++];}for (int j = 0; j < right + 1; j++){a[j] = tmp[j];}
}
void MergeSort(int* a, int size)
{int* tmp = (int*)malloc(sizeof(int) * size);if (tmp == NULL){printf("malloc fail");exit(-1);}_MergeSort(a, 0, size - 1, tmp);free(tmp);tmp = NULL;
}
int main()
{int arr[] = {99,88,66,77,55,44,33,22,11 };MergeSort(arr,sizeof(arr)/sizeof(int));for (int i = 0; i < sizeof(arr) / sizeof(int); i++){printf("%d ", arr[i]);}return 0;
}

运行截图：

归并排序的时间复杂度

时间复杂度：O(N*logN)

稳定性:稳定

排序的稳定性

什么是排序的稳定性呢？

其实就是，在未排序之前，数组中有两个相同的元素（有顺序），如果在排序之后这两个元素的顺序没有发生变化，则称这个排序是稳定的，如果排序之后顺序发生了变化，我们就称这个排序算法是不稳定的。

排序总结

直接插入排序：最好的情况下就是一个有序数组，插入的元素只用跟前面数组的最后一个元素比较，最好复杂度为O(N)。最坏的情况就是一个逆序数组，每个要插入的元素都要和前面的数组元素比较一下，就是等差数列求和O(N^2)
希尔排序：时间复杂度不好计算，大概是O(N^1.3)
选择排序：没有最好和最坏，编译器不知道所以，每个元素都和最小的元素比较一次，一趟排序确定了一元素的位置，剩下的元素下一趟继续进行比较，时间复杂度为等差数列求和O(N^2)
堆排序：没有最好和最坏，因为都是从一个大堆或者小堆进行调整，为O(N*logN)
冒泡排序：有序时，我们有优化，一趟比较下来没有发生交换，所以终止后面的排序，但是第一趟的相邻两个元素都发生了比较，比较了N次，所以最好时间复杂度为O(N),最坏，逆序，等差数列求和O(N^2)
快速排序：最好：每次找到的key都在中间，所以刚好是一个满二叉树，高度为logN，每层比较N次，总共比较N*logN次，所以最好为O(N*logN)
最坏：一个有序数组，每次找的key都在最左边，总共N层，比较等差数列求和次，所以最坏为O(N^2)
归并排序：最好最坏都是O(N*logN)

只有快速排序和归并排序他们俩才会消耗额外额空间，因为递归要频繁的消耗栈帧，且快排非递归实现时运用了栈的数据结构。