这个标题真帅
- Thanks Ni Zihan.
- 随机变量的变换方法总结
- 概率生成函数 (probability-generating function, PGF)
- 矩母函数(Moment Generating Function , MGF)
- 矩母函数详细介绍
- 特征函数
Thanks Ni Zihan.
随机变量的变换方法总结
(Thanks Dr. Ni Zihan,文中所有推导总结来自我的同学倪子涵)
时域信号和频域信号是等价的, 给出时域信号可以算出频域信号, 给出频域信号也可以算出时域信号. 同理拉普拉斯域和时域也是等价的, z 变换域与时域也是等价的. 利用上述三种变换可以简化信号与系统处理的复杂计算量…
那么随机变量的处理中是否也存在着变换的方法呢?
那么使用连续随机变量的概率密度函数的傅里叶变换和拉普拉斯变换以及离散随机变量的概率分布函数的傅里叶变换和 z 变换, 也可以仿照信号与系统的处理手段, 对概率密度函数或者概率分布函数进行简化计算处理.
1/ 连续随机变量的概率密度函数的拉普拉斯变换被称为矩母函数 (Moment Generating Function, MGF). [但是这里有一个小注意事项, 矩母函数定义中所描述的拉普拉斯变换不是我们信号与系统学的拉普拉斯变换公式, 这里的公式需要把信号与系统中拉普拉斯变换中的 e − s t e^{-s t} e−st 改成 e s t ] \left.e^{s t}\right] est]
2/ 离散随机变量的概率分布函数的 z 变换被称为概率生成函数 (Probability Generating Function, PGF). [但是这里有一个小注意事项, 概率生成函数定义中所描述的 z 变换不是我们信号与系统学的 z 变换公式, 需要我们把信号与系统学的 z 变换公式中的 z − n z^{-n} z−n 改成 z n z^{n} zn , 求和下限改成 0 ]
3/ 连续性或离散型随机变量的概率密度函数或概率分布函数的连续时间傅里叶变换或离散时间傅里叶变换成为特征函数 (Characteristic Function, CF). [但是这里有一个小注意事项, 特征函数定义中所描述的傅里叶变换不是我们信号与系统学的傅里叶变换公式, 这里的公式需要把信号与系统中傅里叶变换中的 e − j ω t 改成 e j ω t e^{-j \omega t} 改成 e^{j \omega t} e−jωt改成ejωt , 离散的就是 e − j ω n e^{-j \omega n} e−jωn 改成 e j ω n e^{j \omega n} ejωn.
概率生成函数 (probability-generating function, PGF)
面对这样一个问题,A服从均匀分布,B服从指数分布,C服从另一个高斯分布。则 A*B + C应该是什么分布呢?是否有办法求出其特征的闭式解?
概率生成函数就是这样一个工具,可以用来求解两个连续随机变量乘积的分布。而对于两个连续随机变量和的分布,可以采用卷积公式。
我们已经说过, 离散型 随机变量的概率分布函数的’ z 变换’ 称为概率生成函数, 下面给出定义式 \text { 我们已经说过, 离散型 随机变量的概率分布函数的' } z \text { 变换' 称为概率生成函数, 下面给出定义式 } 我们已经说过, 离散型 随机变量的概率分布函数的’ z 变换’ 称为概率生成函数, 下面给出定义式
G X ( z ) = E [ z X ] = ∑ n = 0 ∞ z n P ( X = n ) = P ( X = 0 ) + z P ( X = 1 ) + z 2 P ( X = 2 ) + ⋯ \begin{aligned} G_{X}(z) & =E\left[z^{X}\right]=\sum_{n=0}^{\infty} z^{n} P(X=n) \\ & =P(X=0)+z P(X=1)+z^{2} P(X=2)+\cdots \end{aligned} GX(z)=E[zX]=n=0∑∞znP(X=n)=P(X=0)+zP(X=1)+z2P(X=2)+⋯
这里我强调一下收玫域. 对于 z 变换, 右边信号的收玫域为 ∣ z ∣ > r |z|>r ∣z∣>r, 左边信号的收玫域为 ∣ z ∣ < r |z|<r ∣z∣<r.我们这里使用的’ z 变换’ 是把 z − n z^{-n} z−n 改成 z n z^{n} zn 的’ z 变换’. 上面的结论也正好反过来, 而且我们的’ z 变换’ 是 n ≥ 0 n \geq 0 n≥0 (理解成右边信号) 的’ 单边 z 变换’, 所以实际上 PGF 的收玫域结构是 ∣ z ∣ < r |z|<r ∣z∣<r . 再加上概率分布函数一定绝对可和, 其必有傅里叶变换, 所以其收玫域必定包含单位圆 ∣ z ∣ = 1 |z|=1 ∣z∣=1 . 综上所述 PGF 的收玫域结构为 ∣ z ∣ < r , r > 1 |z|<r, r>1 ∣z∣<r,r>1 . 我们考虑一下, 一个参数为 λ \lambda λ 的泊松分布的的 PGF:
G X ( z ) = E [ z X ] = ∑ n = 0 ∞ z n P ( X = n ) = ∑ n = 0 ∞ z n λ n e − λ n ! = e − λ ∑ n = 0 ∞ ( z λ ) n n ! = e − λ e z λ = e λ ( z − 1 ) \begin{aligned} G_{X}(z) & =\mathrm{E}\left[z^{X}\right] \\ & =\sum_{n=0}^{\infty} z^{n} \mathrm{P}(X=n) \\ & =\sum_{n=0}^{\infty} z^{n} \frac{\lambda^{n} e^{-\lambda}}{n !} \\ & =e^{-\lambda} \sum_{n=0}^{\infty} \frac{(z \lambda)^{n}}{n !} \\ & =e^{-\lambda} e^{z \lambda}=e^{\lambda(z-1)} \end{aligned} GX(z)=E[zX]=n=0∑∞znP(X=n)=n=0∑∞znn!λne−λ=e−λn=0∑∞n!(zλ)n=e−λezλ=eλ(z−1)
当已知 PGF 的时候, 可以考虑对 PGF 求导以获得概率分布函数:
P ( X = k ) = G X ( k ) ( z ) ∣ z = 0 k ! \mathrm{P}(X=k)=\frac{\left.G_{X}^{(k)}(z)\right|_{z=0}}{k !} P(X=k)=k!GX(k)(z) z=0
这里我必须要强调一件事, 就是说概率分布函数与 PGF 是一对’ z \mathrm{z} z 变换’, 那我们使用’ 逆 z \mathrm{z} z 变换’ 不就可以直接求得概率分布序列了么. 我们不使用’ 逆 z \mathrm{z} z 变换’ 求概率分布的原因有两点: 1 . 逆 z \mathrm{z} z 变换’是一个积分式子不好算; 2.‘z 变换’ 不是严格意义的’ z 变换’, 所以其对应我们在这里需要的所谓的’逆 z \mathrm{z} z 变换’ 公式我们没有. 故, 我们利用求导一个一个算概率分布. PGF 不仅可以求概率分布函数,求解 n 阶矩也是可以滴. 对这个 G X ( z ) G_{X}(z) GX(z) 求一个一阶导数
G X ′ ( z ) = ∑ n = 1 ∞ n z n − 1 P ( X = n ) = ∑ n = 0 ∞ n z n − 1 P ( X = n ) (2.3) G_{X}^{\prime}(z)=\sum_{n=1}^{\infty} n z^{n-1} P(X=n)=\sum_{n=0}^{\infty} n z^{n-1} P(X=n) \tag{2.3} GX′(z)=n=1∑∞nzn−1P(X=n)=n=0∑∞nzn−1P(X=n)(2.3)
然后我们令 z = 1 z = 1 z=1
G X ′ ( 1 ) = ∑ n = 0 ∞ n P ( X = n ) = E [ X ] G_{X}^{\prime}(1)=\sum_{n=0}^{\infty} n P(X=n)=E[X] GX′(1)=n=0∑∞nP(X=n)=E[X]
对公式2.3乘个 z, 再求一阶导数
( z G X ′ ( z ) ) ′ = ∑ n = 0 ∞ n 2 z n − 1 P ( X = n ) \left(z G_{X}^{\prime}(z)\right)^{\prime}=\sum_{n=0}^{\infty} n^{2} z^{n-1} P(X=n) (zGX′(z))′=n=0∑∞n2zn−1P(X=n)
然后我们再令 z = 1
( z G X ′ ( 1 ) ) ′ = ∑ n = 0 ∞ n 2 P ( X = n ) = E [ X 2 ] \left(z G_{X}^{\prime}(1)\right)^{\prime}=\sum_{n=0}^{\infty} n^{2} P(X=n)=E\left[X^{2}\right] (zGX′(1))′=n=0∑∞n2P(X=n)=E[X2]
以此类推, 想求几阶矩就求几阶矩.
PGF 还有一个更牛逼的优势就是它非常适合辅助求解多个独立随机变量和的分布. 假设 Y = X 1 + ⋯ + X n Y= X_{1}+\cdots+X_{n} Y=X1+⋯+Xn , 且 X 1 , ⋯ , X n X_{1}, \cdots, X_{n} X1,⋯,Xn 独立同分布. 利用的就是幕指数乘积的计算特性!
G Y ( z ) = E [ z Y ] = E [ z X 1 + ⋯ + X n ] = E [ z X 1 ] × ⋯ × E [ z X n ] = G X 1 ( z ) × ⋯ × G X n ( z ) \begin{aligned} G_{Y}(z) & =E\left[z^{Y}\right] \\ & =E\left[z^{X_{1}+\cdots+X_{n}}\right] \\ & =E\left[z^{X_{1}}\right] \times \cdots \times E\left[z^{X_{n}}\right] \\ & =G_{X_{1}}(z) \times \cdots \times G_{X_{n}}(z) \end{aligned} GY(z)=E[zY]=E[zX1+⋯+Xn]=E[zX1]×⋯×E[zXn]=GX1(z)×⋯×GXn(z)
如此得到了 Y Y Y 的 PGF, 想求 Y Y Y 的概率分布只需要求导带 0 就可以了.
矩母函数(Moment Generating Function , MGF)
https://zhuanlan.zhihu.com/p/148408669
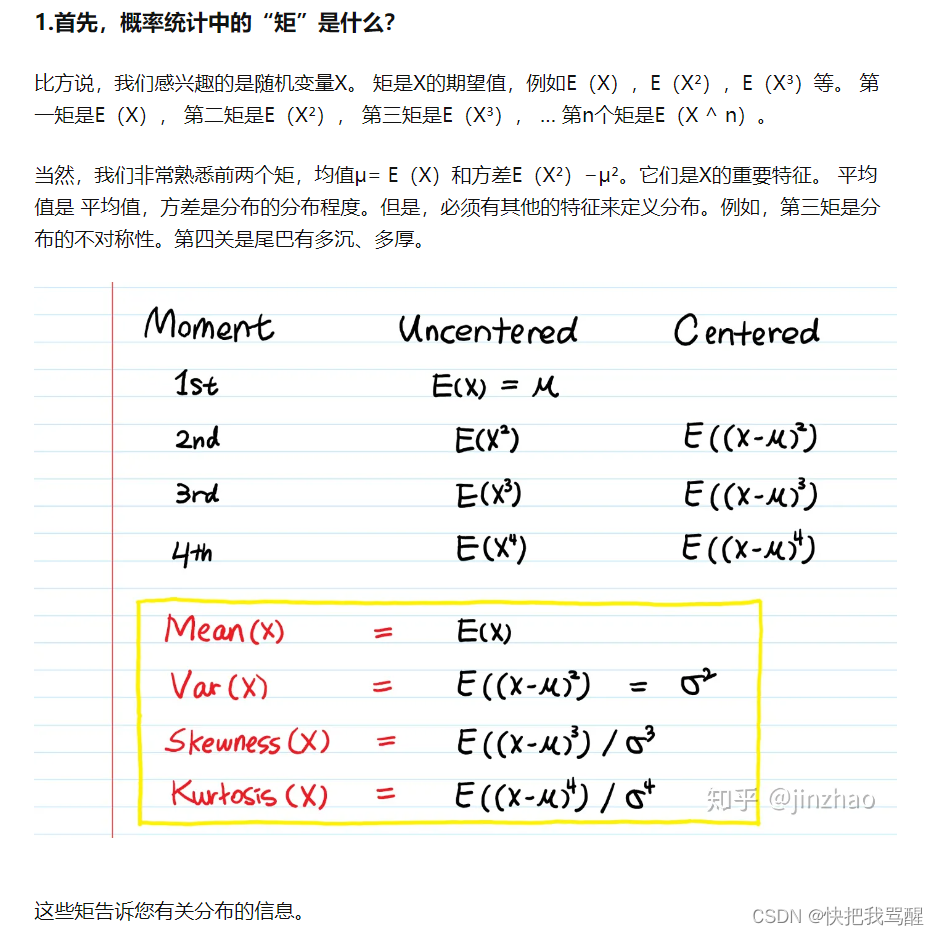


矩母函数详细介绍
我们已经说过, 连续型随机变量的概率密度函数的’ 拉普拉斯变换’ 称为矩母函数, 下面给出定义式
M X ( s ) = E [ e s X ] = ∫ − ∞ + ∞ f X ( x ) e s x d x (2.4) M_{X}(s)=E\left[e^{s X}\right]=\int_{-\infty}^{+\infty} f_{X}(x) e^{s x} d x \tag{2.4} MX(s)=E[esX]=∫−∞+∞fX(x)esxdx(2.4)
MGF 也有收玫域. 右边信号的拉普拉斯变换收玫域结构是 s > a s>a s>a , 左边信号的拉普拉斯变换收玫域结构是 s < a s<a s<a , 双边信号的拉普拉斯变换收玫域是 a 1 < s < a 2 a_{1}<s<a_{2} a1<s<a2 . 由于 e − s t e^{-s t} e−st 改成了 e s t e^{s t} est , 所以对于 MGF 来说, 右拖尾概率密度的 MGF 收玫域结构是 s < a s<a s<a , 左拖尾概率密度的 MGF 收玫域结构是 s > a s>a s>a , 双边拖尾概率密度的 MGF 收玫域是 a 1 < s < a 2 a_{1}<s<a_{2} a1<s<a2 . 由于概率密度函数绝对可积, 其一定有傅里叶变换, 所以 MGF 收玫域必定包括虚轴. 矩母函数可以用来求矩, 求导就行了.
M X ( n ) ( s ) = ∫ − ∞ + ∞ x n f X ( x ) e s x d x M_{X}^{(n)}(s)=\int_{-\infty}^{+\infty} x^{n} f_{X}(x) e^{s x} d x MX(n)(s)=∫−∞+∞xnfX(x)esxdx
令 s = 0 s = 0 s=0 得到利用矩母函数求 n n n 阶矩的公式
M X ( n ) ( 0 ) = ∫ − ∞ + ∞ x n f X ( x ) d x = E [ X n ] M_{X}^{(n)}(0)=\int_{-\infty}^{+\infty} x^{n} f_{X}(x) d x=E\left[X^{n}\right] MX(n)(0)=∫−∞+∞xnfX(x)dx=E[Xn]
当已知一个随机变量的 MGF 的时候, 可以利用现成的拉普拉斯逆变换公式求解概率密度函数
(PDF). 根据公式2.4, 我们知道
M X ( − s ) = E [ e − s X ] = ∫ − ∞ + ∞ f X ( x ) e − s x d x M_{X}(-s)=E\left[e^{-s X}\right]=\int_{-\infty}^{+\infty} f_{X}(x) e^{-s x} d x MX(−s)=E[e−sX]=∫−∞+∞fX(x)e−sxdx
即, M X ( − s ) M_{X}(-s) MX(−s) 是 f X ( x ) f_{X}(x) fX(x) 的拉普拉斯变换. 我们只要对 M X ( − s ) M_{X}(-s) MX(−s) 做拉普拉斯逆变换就可以得到概率密度函数 f X ( x ) f_{X}(x) fX(x) . 但要注意, s → − s s \rightarrow-s s→−s , 收玫域也要反过来. 最后要说的就是利用指数的计算特性以及矩母函数求解多个独立随机变量和的概率密度函数. 假设 Y = X 1 + ⋯ + X n Y=X_{1}+\cdots+X_{n} Y=X1+⋯+Xn , 且 X 1 , ⋯ , X n X_{1}, \cdots, X_{n} X1,⋯,Xn 独立同分布. 我们有
M Y ( s ) = E [ e s Y ] = E [ e s ( X 1 + ⋯ + X n ) ] = E [ e s X 1 ] × ⋯ × E [ e s X n ] = M X 1 ( s ) × ⋯ × M X n ( s ) \begin{aligned} M_{Y}(s) & =E\left[e^{s Y}\right] \\ & =E\left[e^{s\left(X_{1}+\cdots+X_{n}\right)}\right] \\ & =E\left[e^{s X_{1}}\right] \times \cdots \times E\left[e^{s X_{n}}\right] \\ & =M_{X_{1}}(s) \times \cdots \times M_{X_{n}}(s) \end{aligned} MY(s)=E[esY]=E[es(X1+⋯+Xn)]=E[esX1]×⋯×E[esXn]=MX1(s)×⋯×MXn(s)
然后对 M Y ( − s ) 做逆拉普拉斯变换就可以得到 Y 的概率密度函数辣, 但别忘了收玫域的事儿. \text { 然后对 } M_{Y}(-s) \text { 做逆拉普拉斯变换就可以得到 } Y \text { 的概率密度函数辣, 但别忘了收玫域的事儿. } 然后对 MY(−s) 做逆拉普拉斯变换就可以得到 Y 的概率密度函数辣, 但别忘了收玫域的事儿.
特征函数
有没有一种统一形式可以同时定义离散和连续随机变量的某种函数, 且也能实现便利计算的特性
呢? 有! 利用傅里叶变换产生的特征函数! 特征函数定义为
φ X ( ω ) = E [ e j ω X ] = { ∫ − ∞ + ∞ f X ( x ) e j ω x d x 连续 ∑ n = − ∞ + ∞ P ( X = n ) e j ω x 离散 \varphi_{X}(\omega)=E\left[e^{j \omega X}\right]=\left\{\begin{array}{ll} \int_{-\infty}^{+\infty} f_{X}(x) e^{j \omega x} d x & \text { 连续 } \\ \sum_{n=-\infty}^{+\infty} P(X=n) e^{j \omega x} & \text { 离散 } \end{array}\right. φX(ω)=E[ejωX]={∫−∞+∞fX(x)ejωxdx∑n=−∞+∞P(X=n)ejωx 连续 离散
特征函数的反变换就能求得概率密度函数或者概率分布函数
f ( x ) = 1 2 π ∫ − ∞ + ∞ φ X ( ω ) e − j ω x d ω P ( X = n ) = 1 2 π ∫ 2 π φ X ( ω ) e − j ω x d ω \begin{array}{r} f(x)=\frac{1}{2 \pi} \int_{-\infty}^{+\infty} \varphi_{X}(\omega) e^{-j \omega x} d \omega \\ P(X=n)=\frac{1}{2 \pi} \int_{2 \pi} \varphi_{X}(\omega) e^{-j \omega x} d \omega \end{array} f(x)=2π1∫−∞+∞φX(ω)e−jωxdωP(X=n)=2π1∫2πφX(ω)e−jωxdω
任何一个概率密度函数或者概率分布函数不一定有 PGF 或 MGF, 但是由于他们本身的绝对可积
或者绝对可和, 他们一定有特征函数. 所以 PGF,MGF 不好使的时候, 可以用特征函数. 对特征函
数求导再带定值也可以得到 n 阶矩
E [ X n ] = φ X n ( ω ) ∣ ω = 0 j n E\left[X^{n}\right]=\frac{\left.\varphi_{X}^{n}(\omega)\right|_{\omega=0}}{j^{n}} E[Xn]=jnφXn(ω)∣ω=0
利用特征函数以及幕指数的计算特性可以求解多个独立随机变量和的概率密度函数或者概率分布函数. 假设 Y = X 1 + ⋯ + X n Y=X_{1}+\cdots+X_{n} Y=X1+⋯+Xn , 且 X 1 , ⋯ , X n X_{1}, \cdots, X_{n} X1,⋯,Xn 独立同分布. 我们有
φ Y ( ω ) = E [ e j ω Y ] = E [ e j ω ( X 1 + ⋯ + X n ) ] = E [ e j ω X 1 ] × ⋯ × E [ e j ω X n ] = φ X 1 ( ω ) × ⋯ × φ X n ( ω ) \begin{aligned} \varphi_{Y}(\omega) & =E\left[e^{j \omega Y}\right] \\ & =E\left[e^{j \omega\left(X_{1}+\cdots+X_{n}\right)}\right] \\ & =E\left[e^{j \omega X_{1}}\right] \times \cdots \times E\left[e^{j \omega X_{n}}\right] \\ & =\varphi_{X_{1}}(\omega) \times \cdots \times \varphi_{X_{n}}(\omega) \end{aligned} φY(ω)=E[ejωY]=E[ejω(X1+⋯+Xn)]=E[ejωX1]×⋯×E[ejωXn]=φX1(ω)×⋯×φXn(ω)
’ 频域’ 乘积, 时域就得卷积, 可以得到 Y Y Y 的概率密度函数或概率分布函数为
f Y ( x ) = f X 1 ( x ) ∗ f X 2 ( x ) ∗ ⋯ ∗ f X n ( x ) P ( Y = k ) = P ( X 1 = k ) ∗ P ( X 2 = k ) ∗ ⋯ ∗ P ( X n = k ) \begin{array}{l} f_{Y}(x)=f_{X_{1}}(x) * f_{X_{2}}(x) * \cdots * f_{X_{n}}(x) \\ P(Y=k)=P\left(X_{1}=k\right) * P\left(X_{2}=k\right) * \cdots * P\left(X_{n}=k\right) \end{array} fY(x)=fX1(x)∗fX2(x)∗⋯∗fXn(x)P(Y=k)=P(X1=k)∗P(X2=k)∗⋯∗P(Xn=k)