【详解优先级队列(堆)】

堆的概念

堆的性质

堆的存储方式

堆的创建

堆的向下调整

向下过程(以小堆为例)

向下过程(以大堆为例)

建堆的时间复杂度O(n)

堆的插入与删除

堆的插入

向上调整建堆的时间复杂度O(nlogn)

堆的删除

常见习题

常用接口介绍

PriorityQueue的特性

PriorityQueue常用接口介绍

优先级队列的构造

插入/删除/获取优先级最高的元素

oj练习

堆的应用

1.PriorityQueue的实现

2.堆排序

🌠作者：@TheMythWS.

🎇座右铭：不走心的努力都是在敷衍自己，让自己所做的选择，熠熠发光。

之前我们介绍过队列，队列是一种先进先出(FIFO)的数据结构，但有些情况下，操作的数据可能带有优先级，一般出队列时，可能需要优先级高的元素先出队列，该场景下，使用队列显然不合适，比如：在手机上玩游戏的时候，如果有来电，那么系统应该优先处理打进来的电话；初中那会班主任排座位时可能会让成绩好的同学先挑座位。
在这种情况下，数据结构应该提供两个最基本的操作，一个是返回最高优先级对象，一个是添加新的对象。这种数据结构就是优先级队列(Priority Queue)。

优先级队列的模拟实现
JDK1.8中的PriorityQueue底层使用了堆这种数据结构，而堆实际就是在完全二叉树的基础上进行了一些调整。所以我们先要了解堆这个数据结构。

堆的概念

如果有一个关键码的集合K = {k0，k1， k2，…，kn-1}，把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中，并满足：Ki <= K2i+1 且 Ki<= K2i+2 (Ki >= K2i+1 且 Ki >= K2i+2) i = 0，1，2…，则称为小堆(或大堆)。

将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆.

堆的性质

堆中某个节点的值总是不大于（<=）或不小于（>=）其父节点的值；
堆总是一棵完全二叉树。

堆的存储方式

从堆的概念可知，堆是一棵完全二叉树，因此可以层序的规则采用顺序的方式来高效存储。

注意：对于非完全二叉树，则不适合使用顺序方式进行存储，因为为了能够还原二叉树，空间中必须要存储空节点，就会导致空间利用率比较低。

将元素存储到数组中后，可以根据二叉树章节的性质5对树进行还原。假设i为节点在数组中的下标，则有：
如果i为0，则i表示的节点为根节点，否则i节点的双亲节点为 (i - 1)/2
如果2 * i + 1 小于节点个数，则节点i的左孩子下标为2 * i + 1，否则没有左孩子
如果2 * i + 2 小于节点个数，则节点i的右孩子下标为2 * i + 2，否则没有右孩子

堆的创建

堆的向下调整

对于集合{ 27, 15, 19, 18, 28, 34, 65, 49, 25, 37 }中的数据，如果将其创建成堆呢？

仔细观察上图后发现：根节点的左右子树已经完全满足堆的性质，因此只需将根节点向下调整好即可。（每棵子树都是从根节点向下调整）

向下过程(以小堆为例)

方法：
1. 让parent标记需要调整的节点，child标记parent的左孩子(注意：parent如果有孩子一定先是有左孩子)
2. 如果parent的左孩子存在，即:child < size，进行以下操作，直到parent的左孩子不存在
parent右孩子是否存在，存在找到左右孩子中最小的孩子，让child进行标记, 将parent与较小的孩子child比较，如果：
(1)parent小于较小的孩子child，调整结束;
(2)否则：交换parent与较小的孩子child，交换完成之后，parent中大的元素向下移动，可能导致子树不满足堆的性质，因此需要继续向下调整，即parent = child；child = parent*2+1; 然后继续2步骤。

图解：

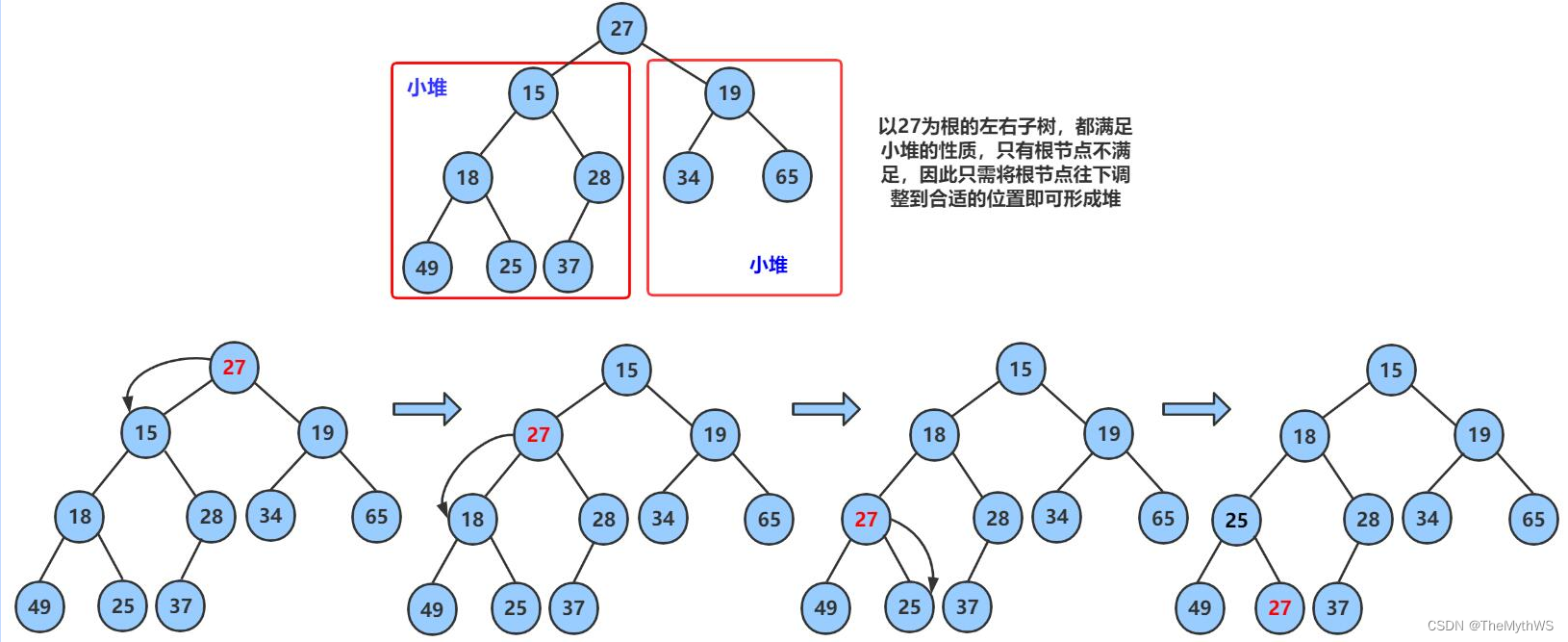
向下过程(以大堆为例)

从最后一棵子树的根节点开始调整

简单来说就是如果要创建一个小（大）根堆，那么要先满足它的左子树和右子树都是小（大）根堆。

public class TestHeap {public int[] elem;public int usedSize;public TestHeap() {this.elem = new int[10];}public void initElem(int[] array) {for (int i = 0; i < array.length; i++) {elem[i] = array[i];usedSize++;}}public void createBigHeap() {//以大堆为例://找倒数第一个非叶子节点，从该节点位置开始往前一直到根节点，遇到一个节点，应用向下调整 : 每棵树都是从父节点开始往下走.for (int parent = (usedSize - 1 - 1) / 2; parent >= 0; parent--) {bigShiftDown(parent, usedSize);}}/*父亲下标(当前每棵树的节点数)每棵树的结束下标*///时间复杂度分析: 最坏情况: 从根一路比较到叶子, 比较的次数为完全二叉树的高度, 即O(logn)private void bigShiftDown(int parent, int len) {//parent每棵子树的根节点，len每棵子树调整的结束位置，不能 > len// child先标记parent的左孩子，因为parent可能有左孩子, 没有右孩子(至少有左孩子)int child = 2 * parent + 1;//最起码要有左孩子while (child < len) {//假设len = 10, child最多只能等于9下标, 因为没有10下标.// 如果右孩子存在，找到左右孩子中较大的孩子,用child进行标记if (child + 1 < len && elem[child] < elem[child + 1]) {child++;}//child下标 一定是左右孩子最大值的下标//如果双亲比其最大的孩子还小，将双亲和最大的孩子交换if (elem[child] > elem[parent]) {int tmp = elem[child];elem[child] = elem[parent];elem[parent] = tmp;//parent小，往下移动，可能会造成子树不满足堆的性质，因此需要继续向下调整parent = child;child = 2 * parent + 1;} else {//双亲比其最大的孩子还大, 说明该结构已经满足大堆的特性了break;}}}public void createSmallHeap() {//以小堆为例://找倒数第一个非叶子节点，从该节点位置开始往前一直到根节点，遇到一个节点，应用向下调整 : 每棵树都是从父节点开始往下走.for (int parent = (usedSize - 1 - 1) / 2; parent >= 0; parent--) {smallShiftDown(parent, usedSize);}}/*父亲下标(当前每棵树的节点数)每棵树的结束下标*///时间复杂度分析: 最坏情况: 从根一路比较到叶子, 比较的次数为完全二叉树的高度, 即O(logn)private void smallShiftDown(int parent, int len) {// child先标记parent的左孩子，因为parent可能有左孩子, 没有右孩子(至少有左孩子)int child = 2 * parent + 1;//最起码要有左孩子while (child < len) {//假设len = 10, child最多只能等于9下标, 因为没有10下标.// 如果右孩子存在，找到左右孩子中较小的孩子,用child进行标记if (child + 1 < len && elem[child] > elem[child + 1]) {child++;}//child下标 一定是左右孩子最小值的下标//如果双亲比其最小的孩子还大，将双亲和最小的孩子交换if (elem[child] < elem[parent]) {int tmp = elem[child];elem[child] = elem[parent];elem[parent] = tmp;//parent大，往下移动，可能会造成子树不满足堆的性质，因此需要继续向下调整parent = child;child = 2 * parent + 1;} else {//双亲比其最小的孩子还小, 说明该结构已经满足小堆的特性了break;}}}   
}

注意：在调整以parent为根的二叉树时，必须要满足parent的左子树和右子树已经是堆了才可以向下调整。

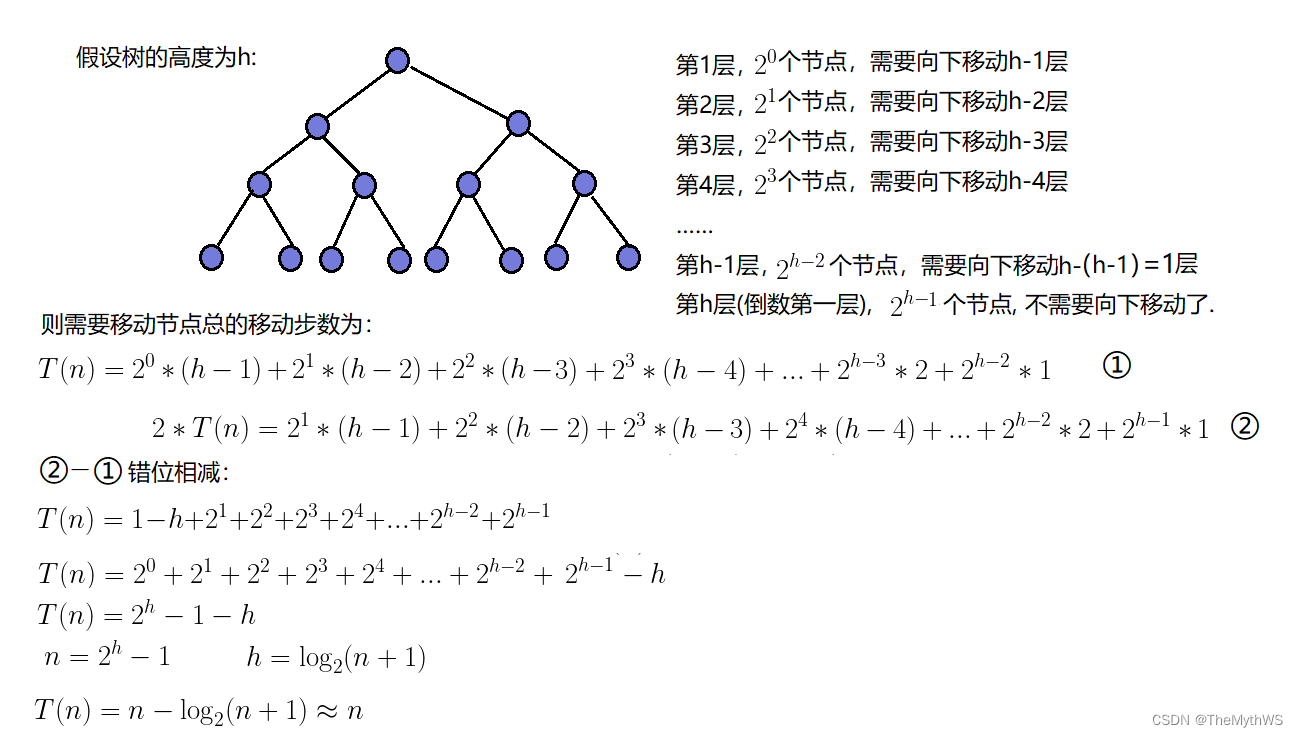
建堆的时间复杂度O(n)

因为堆是完全二叉树，而满二叉树也是完全二叉树，此处为了简化使用满二叉树来证明(时间复杂度本来看的就是近似值，多几个节点不影响最终结果)：

堆的插入与删除

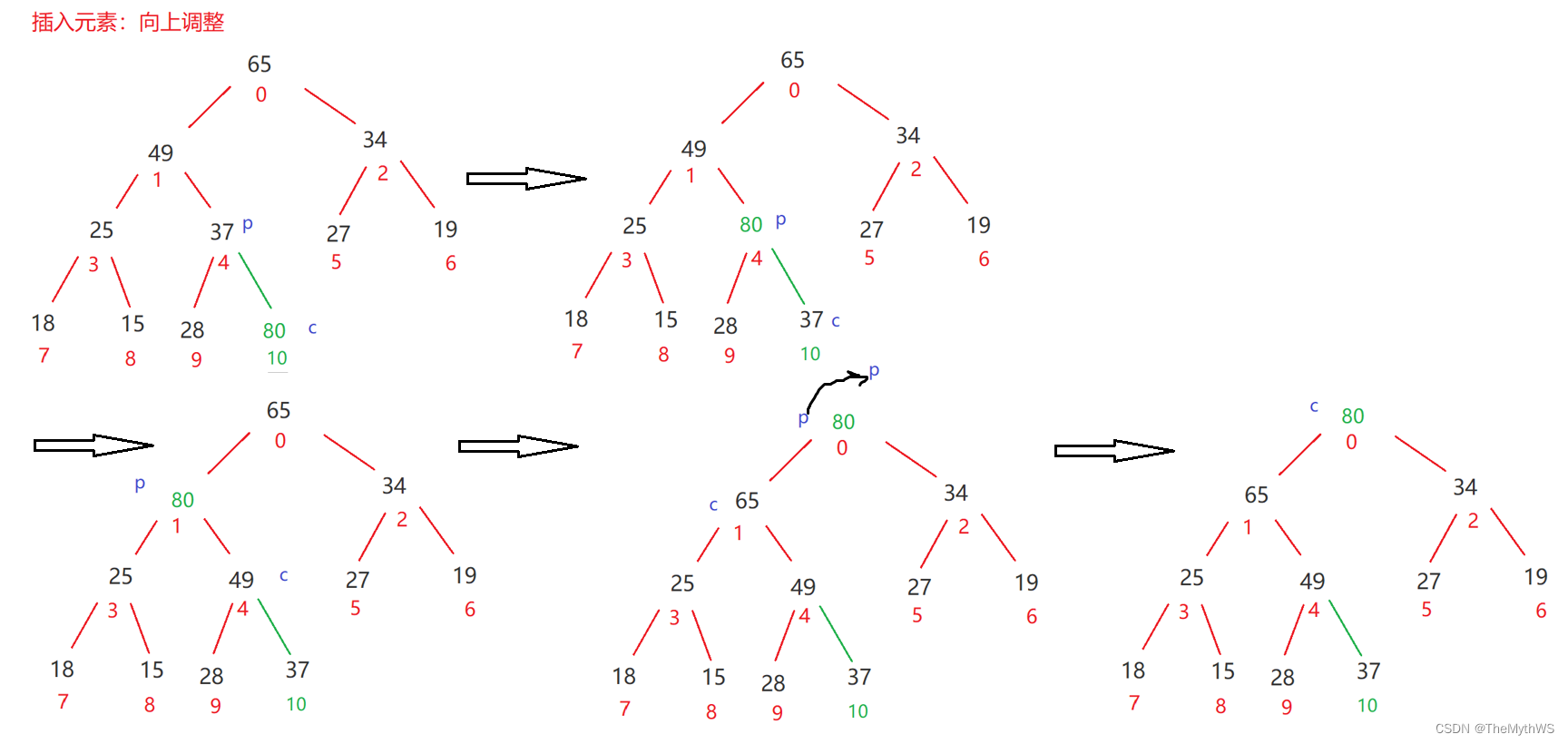
堆的插入

堆的插入总共需要两个步骤：
1. 先将元素放入到底层空间中(注意：空间不够时需要扩容)
2. 将最后新插入的节点向上调整，直到满足堆的性质

这里是向上调整！！！跟上面的向下调整注意区分开

向上调整：从最后一个孩子(即刚插入的节点)从上顺着双亲结点调整
向下调整：从最后一颗子树的双亲节点向下调整

以小堆为例:

以大堆为例:

//堆的插入(大堆)//向上调整建堆 时间复杂度:O(nlogn)public void bigOffer(int val) {if (isFull()) {//扩容elem = Arrays.copyOf(elem, 2 * elem.length);}
//        elem[usedSize] = val;
//        usedSize++;elem[usedSize++] = val;//向上调整bigShiftUp(usedSize - 1);//因为usdSize刚刚已经+1了, 所以最后一个节点下标是usedSize - 1}//向上调整, 以大堆为例private void bigShiftUp(int child) {int parent = (child - 1) / 2;while (child > 0) {//如果新插入的节点比双亲节点大, 就交换它们的值if (elem[child] > elem[parent]) {int tmp = elem[child];elem[child] = elem[parent];elem[parent] = tmp;child = parent;parent = (child - 1) / 2;} else {//比双亲节点还小, 满足大堆的性质, 不需要调整了.break;}}}//堆的插入(小堆)//向上调整建堆 时间复杂度:O(nlogn)public void smallOffer(int val) {if (isFull()) {//扩容elem = Arrays.copyOf(elem, 2 * elem.length);}
//        elem[usedSize] = val;
//        usedSize++;elem[usedSize++] = val;//向上调整smallShiftUp(usedSize - 1);//因为usdSize刚刚已经+1了, 所以最后一个节点下标是usedSize - 1}//向上调整, 以小堆为例private void smallShiftUp(int child) {int parent = (child - 1) / 2;while (child > 0) {//如果新插入的节点比双亲节点小, 就交换它们的值if (elem[child] < elem[parent]) {int tmp = elem[child];elem[child] = elem[parent];elem[parent] = tmp;child = parent;parent = (child - 1) / 2;} else {//比双亲节点还小, 满足大堆的性质, 不需要调整了.break;}}}public boolean isFull() {return usedSize == elem.length;}

public static void main(String[] args) {TestHeap testHeap = new TestHeap();int[] arr = {27, 15, 19, 18, 28, 34, 65, 49, 25, 37};testHeap.initElem(arr);
//        testHeap.createBigHeap();
//        testHeap.bigOffer(80);testHeap.createSmallHeap();testHeap.smallOffer(10);System.out.println("断点调试");}

大堆插入:

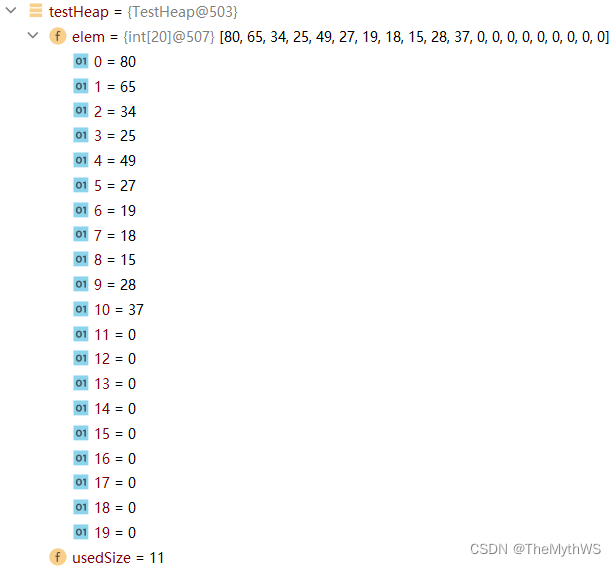
小堆的插入:

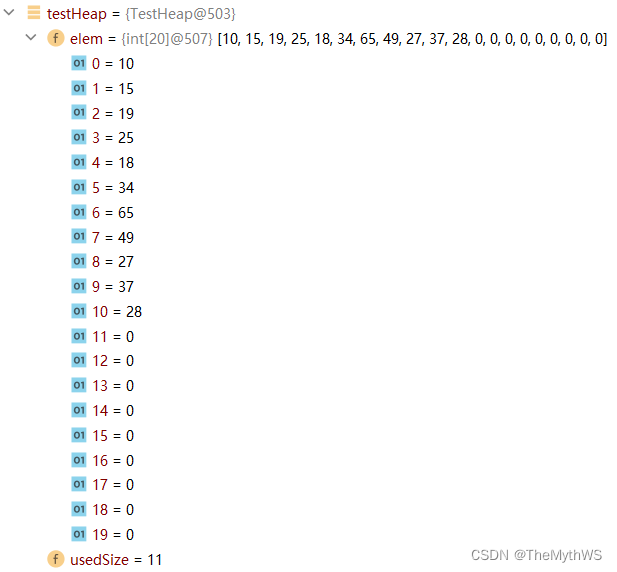
向上调整建堆的时间复杂度O(nlogn)

堆的删除

注意：堆的删除一定删除的是堆顶元素。具体如下：
1. 将堆顶元素对堆中最后一个元素交换
2. 将堆中有效数据个数减少一个
3. 对堆顶元素进行向下调整

插入10之后的小堆的删除

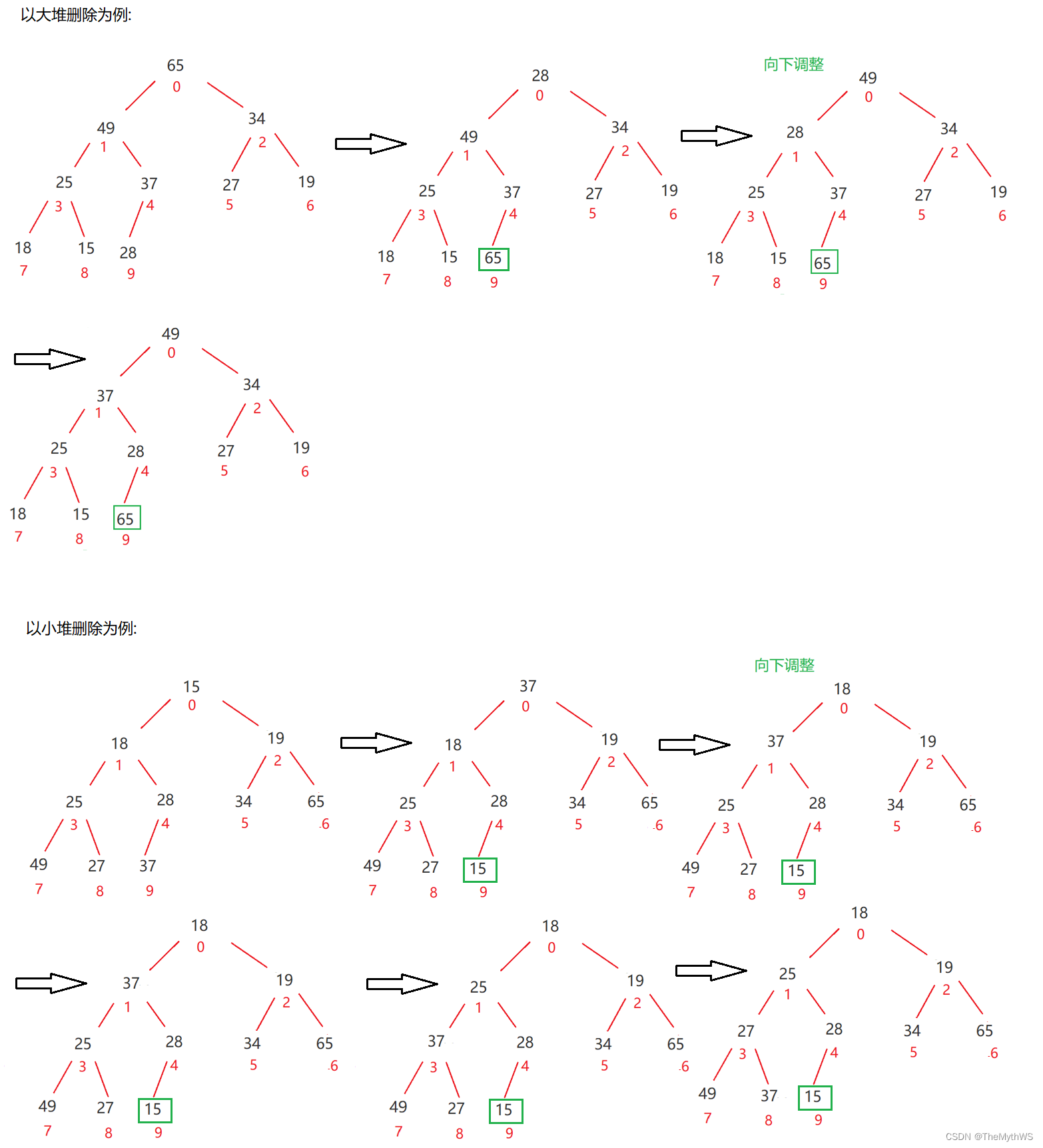
 //堆的删除(大堆)public void bigPoll() {if (isEmpty()) {return;}swap(elem, 0, usedSize - 1);usedSize--;bigShiftDown(0, usedSize);}//堆的删除(小堆)public void smallPoll() {if (isEmpty()) {return;}swap(elem, 0, usedSize - 1);usedSize--;smallShiftDown(0, usedSize);}private void swap(int[] array, int i, int j) {int tmp = elem[i];elem[i] = elem[j];elem[j] = tmp;}public boolean isEmpty() {return usedSize == 0;}

public static void main(String[] args) {TestHeap testHeap = new TestHeap();int[] arr = {27, 15, 19, 18, 28, 34, 65, 49, 25, 37};testHeap.initElem(arr);testHeap.createBigHeap();testHeap.bigPoll();
//        testHeap.createSmallHeap();
//        testHeap.smallPoll();System.out.println("断点调试");}

常见习题

1.下列关键字序列为堆的是:()
A: 100,60,70,50,32,65 B: 60,70,65,50,32,100 C: 65,100,70,32,50,60
D: 70,65,100,32,50,60 E: 32,50,100,70,65,60 F: 50,100,70,65,60,32

2.已知小根堆为8,15,10,21,34,16,12，删除关键字8之后需重建堆，在此过程中，关键字之间的比较次数是()

A: 1 B: 2 C: 3 D: 4

3.最小堆[0,3,2,5,7,4,6,8],在删除堆顶元素0之后，其结果是()
A: [3，2，5，7，4，6，8] B: [2，3，5，7，4，6，8]
C: [2，3，4，5，7，8，6] D: [2，3，4，5，6，7，8]

注意:
大小堆的插入是向上调整，删除和创建是向下调整。
插入和删除元素的时间复杂度为O(logn)
建堆的时间复杂度为O(n)

常用接口介绍

PriorityQueue的特性

Java集合框架中提供了PriorityQueue和PriorityBlockingQueue两种类型的优先级队列，
PriorityQueue是线程不安全的，PriorityBlockingQueue是线程安全的，本文主要介绍PriorityQueue。

关于PriorityQueue的使用要注意：

使用时必须导入PriorityQueue所在的包，即: import java.util.PriorityQueue;
PriorityQueue中放置的元素必须要能够比较大小，不能插入无法比较大小的对象，否则会抛出ClassCastException异常
不能插入null对象，否则会抛出NullPointerException
没有容量限制，可以插入任意多个元素，其内部可以自动扩容
插入和删除元素的时间复杂度为O(logn)
PriorityQueue底层使用了堆数据结构
PriorityQueue默认情况下是小堆---即每次获取到的元素都是最小的元素

PriorityQueue常用接口介绍

优先级队列的构造

此处只是列出了PriorityQueue中常见的几种构造方式

public static void main(String[] args) {// 创建一个空的优先级队列，底层默认容量是11PriorityQueue<Integer> q1 = new PriorityQueue<>();// 创建一个空的优先级队列，底层的容量为initialCapacityPriorityQueue<Integer> q2 = new PriorityQueue<>(100);ArrayList<Integer> list = new ArrayList<>();list.add(4);list.add(3);list.add(2);list.add(1);// 用ArrayList对象来构造一个优先级队列的对象// q3中已经包含了三个元素PriorityQueue<Integer> q3 = new PriorityQueue<>(list);System.out.println(q3.size());//4System.out.println(q3.peek());//1
}

注意：默认情况下，PriorityQueue队列是小堆，如果需要大堆需要用户提供比较器

// 用户自己定义的比较器：直接实现Comparator接口，然后重写该接口中的compare方法即可
class IntCmp implements Comparator<Integer> {@Overridepublic int compare(Integer o1, Integer o2) {return o2 - o1;//大--->小}
}
public static void main(String[] args) {PriorityQueue<Integer> p = new PriorityQueue<>(new IntCmp());p.offer(4);p.offer(3);p.offer(2);p.offer(1);p.offer(5);System.out.println(p.peek());//5//此时创建出来的就是一个大堆。}

插入/删除/获取优先级最高的元素

public static void main(String[] args) {int[] arr = {4, 1, 9, 2, 8, 0, 7, 3, 6, 5};// 一般在创建优先级队列对象时，如果知道元素个数，建议就直接将底层容量给好// 否则在插入时需要不多的扩容// 扩容机制：开辟更大的空间，拷贝元素，这样效率会比较低PriorityQueue<Integer> q = new PriorityQueue<>(arr.length);for (int e : arr) {q.offer(e);}System.out.println(q.size()); //10 打印优先级队列中有效元素个数System.out.println(q.peek()); //0 获取优先级最高的元素// 从优先级队列中删除两个元素之后，再次获取优先级最高的元素q.poll();q.poll();System.out.println(q.size()); //8 打印优先级队列中有效元素个数System.out.println(q.peek()); //2 获取优先级最高的元素q.offer(0);System.out.println(q.peek()); //0 获取优先级最高的元素// 将优先级队列中的有效元素删除掉，检测其是否为空q.clear();if (q.isEmpty()) {System.out.println("优先级队列已经为空!!!");} else {System.out.println("优先级队列不为空");}}

注意：以下是JDK 1.8中，PriorityQueue的扩容方式：

优先级队列的扩容说明:

如果容量小于64时，是按照oldCapacity的2倍方式扩容的
如果容量大于等于64，是按照oldCapacity的1.5倍方式扩容的
如果容量超过MAX_ARRAY_SIZE，按照MAX_ARRAY_SIZE来进行扩容

oj练习

top-k问题：最大或者最小的前k个数据。比如：世界前500强公司

top-k问题最小k个数

//top-k问题:最小的前k个值//普通做法:public int[] smallestK(int[] arr, int k) {//O(nlogn + klogn = (n+k)logn ≈ nlogn)int[] ret = new int[k];// 参数检测if (null == arr || k <= 0) {//return new int[0];return ret;}Queue<Integer> minHeap = new PriorityQueue<>(arr.length);// 将数组中的元素依次放到堆中 O(nlogn)for (int x : arr) {minHeap.offer(x);}// 将优先级队列的前k个元素放到数组中 O(klogn)for (int i = 0; i < k; i++) {ret[i] = minHeap.poll();}return ret;}

以上解法只是PriorityQueue的简单使用，并不是topK最好的做法，那top-k该如何实现？
TOP-K问题：即求数据集合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。
比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题，能想到的最简单直接的方式就是排序，但是：如果数据量非常大，排序就不太可取了(可能数据都不能一下子全部加载到内存中)。
最佳的方式就是用堆来解决，基本思路如下：

1. 用数据集合中前K个元素来建堆
前k个最大的元素，则建小堆
前k个最小的元素，则建大堆
2. 用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素
将剩余N-K个元素依次与堆顶元素比完之后，堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
实现思路:

下面以top-k前k个最大值的做法为例:

//top-k问题:最大的前k个值 O(nlogk)//比较好的解法public static int[] largestK(int[] arr, int k) {int[] ret = new int[k];// 参数检测if (null == arr || k <= 0) {//return new int[0];return ret;}Queue<Integer> minHeap = new PriorityQueue<>(k);// 1.将数组中的前k个元素依次放到堆中, 前k个建立小根堆 O(klogk)for (int i = 0; i < k; i++) {minHeap.offer(arr[i]);}// 2.遍历剩下个元素, 每次和堆顶元素作比较 O((n-k)*logk)// 因为是小根堆, 堆顶元素是最小的, 当遍历到数组元素大于堆顶的时候，说明此时堆顶的元素一定不是前K个最大的值。入堆,调整堆//否则,不入堆.for (int i = k; i < arr.length; i++) {int topValue = minHeap.peek();if (arr[i] > topValue) {minHeap.poll();minHeap.offer(arr[i]);}}// 3.将前k个元素放到数组中 O(klogn)for (int i = 0; i < k; i++) {ret[i] = minHeap.poll();}return ret;}
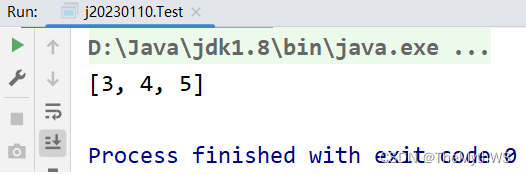
public static void main(String[] args) {int[] array = {1, 2, 3, 4, 5};int[] ret = largestK(array, 3);System.out.println(Arrays.toString(ret));}

堆的应用

1.PriorityQueue的实现

用堆作为底层结构封装优先级队列

2.堆排序

堆排序即利用堆的思想来进行排序，总共分为两个步骤：
(1) 建堆
升序：建大堆
降序：建小堆

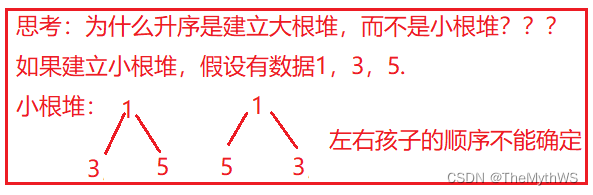
(2)利用堆删除思想来进行排序
建堆和堆删除中都用到了向下调整，因此掌握了向下调整，就可以完成堆排序。

以升序为列子:

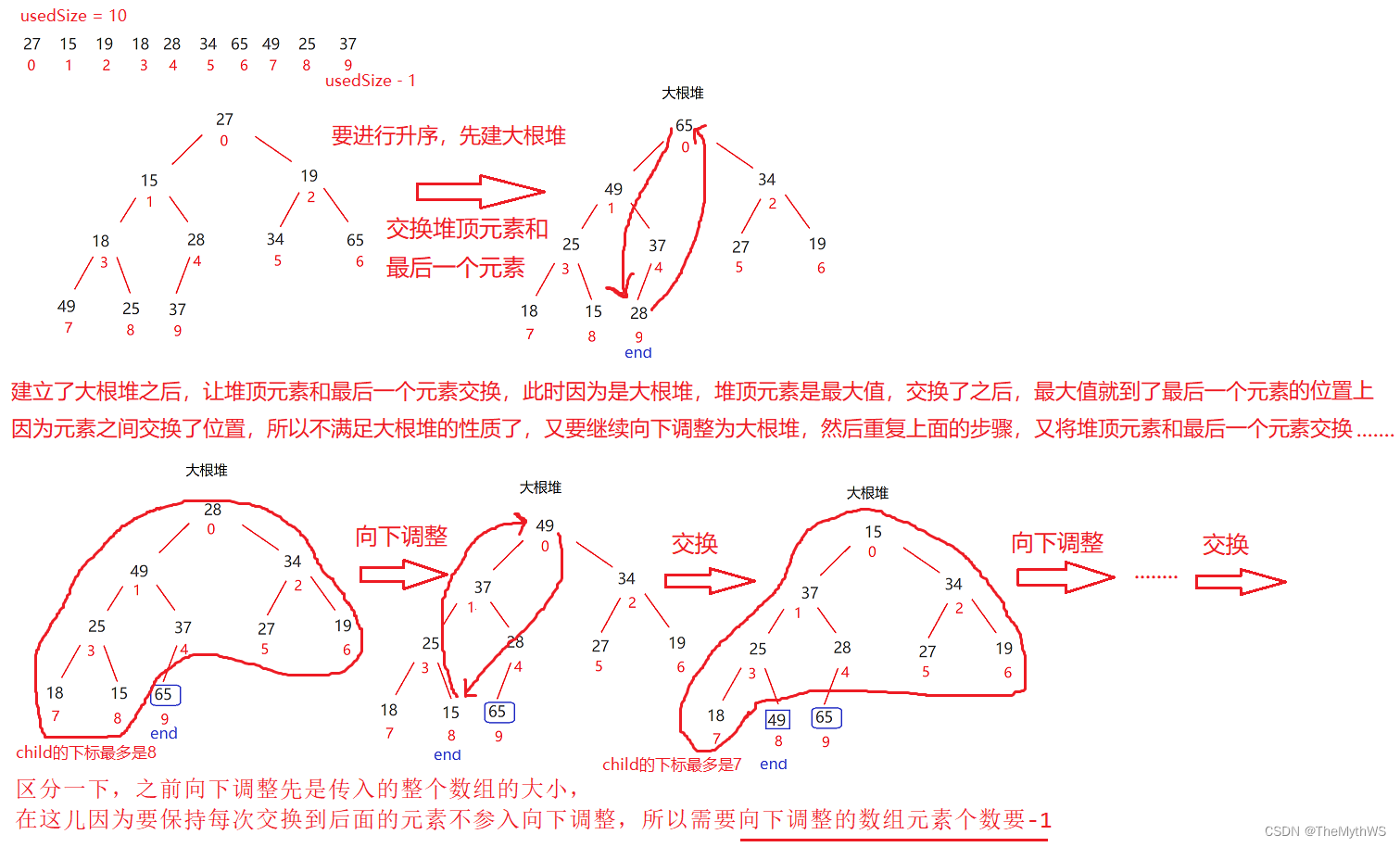
 //堆排序:升序 (建大堆, 大堆向下调整)//时间复杂度:O(nlogn) 空间复杂度:O(1)public void heapAscSort() {int end = usedSize - 1;while (end > 0) {swap(elem, 0, end);bigShiftDown(0, end);/*区分一下，之前向下调整先是传入的整个数组的大小，在这儿因为要保持每次交换到后面的元素不参入向下调整，所以需要向下调整的数组元素个数要-1*/end--;}}//堆排序:降序 (建小堆, 小堆向下调整)//时间复杂度:O(nlogn) 空间复杂度:O(1)public void heapDescSort() {int end = usedSize - 1;while (end > 0) {swap(elem, 0, end);smallShiftDown(0, end);/*区分一下，之前向下调整先是传入的整个数组的大小，在这儿因为要保持每次交换到后面的元素不参入向下调整，所以需要向下调整的数组元素个数要-1*/end--;}
}
public static void main(String[] args) {TestHeap testHeap = new TestHeap();int[] arr = {27, 15, 19, 18, 28, 34, 65, 49, 25, 37};testHeap.initElem(arr);//testHeap.createBigHeap();//testHeap.heapAscSort();testHeap.createSmallHeap();testHeap.heapDescSort();System.out.println("断点调试");
}

常见习题

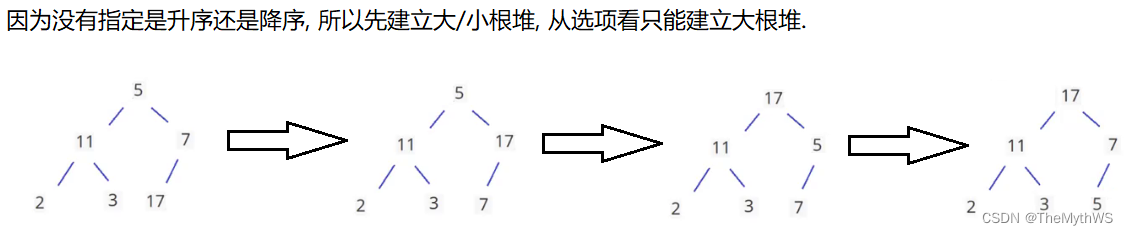
一组记录排序码为(5 11 7 2 3 17)，则利用堆排序方法建立的初始堆为()
A: (11 5 7 2 3 17) B: (11 5 7 2 17 3) C: (17 11 7 2 3 5)
D: (17 11 7 5 3 2) E: (17 7 11 3 5 2) F: (17 7 11 3 2 5)