文章目录
- 1、运用场景
- 2、图形描述相关性
- 2.1使用场景
- 2.2 代码实现
- 2.3 效果呈现
- 3、正态资料相关性分析
- 3.1 使用场景
- 3.2 皮尔森相关系数
- 3.3 代码实现
- 3.4 结果分析
- 4、非正太资料的相关分析
- 4.1 使用场景
- 4.2 斯皮尔曼等级相关系数
- 4.3 代码实现
- 4.4 结果分析
1、运用场景
相关性分析是研究两个或两个以上随机变量间相关关系的统计方法。在数据分析中,它常用于分析连续型自变量X与连续型因变量Y之间的关系。在待分析特征较少时,可使用做图法分析,特征较多时,可使用皮尔森或者斯皮尔曼等工具分析,这这些只能判断线性关系,如果要判断非线性关系,则可将连续数组分组以后使用方差分析对比各组之间的差异。
2、图形描述相关性
2.1使用场景
待分析的特征较少
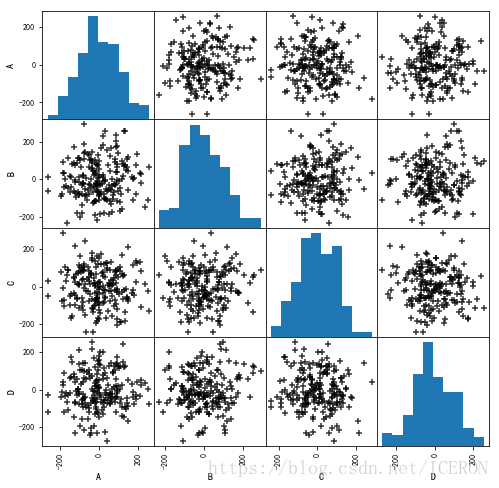
散点图是在两变量相关性分析分析时最常用的展示方法。如下图所示。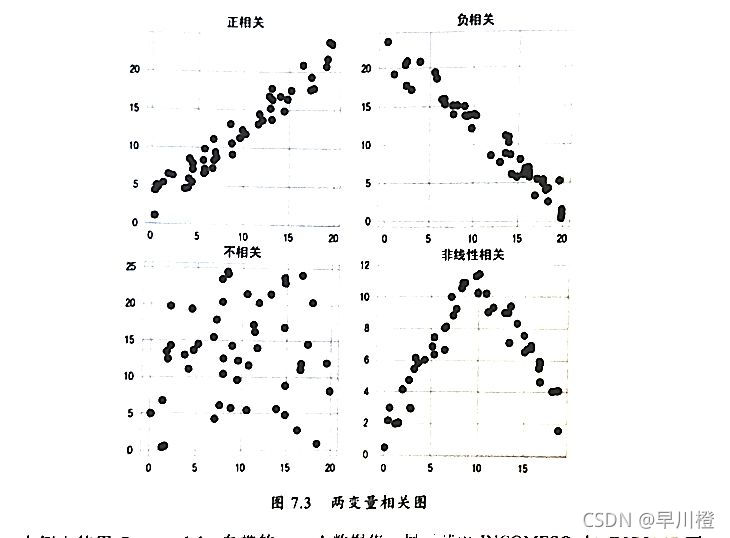
本文使用Statsmodels 自带的 ccard数据集, 展示其中的INCOMESQ与IMCOME两个变量的相关性
2.2 代码实现
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt
from statsmodels.datasets import ccarddata = ccard.load_pandas().data
print(data)
plt.scatter(data['INCOMESQ'],data['INCOME'])
plt.grid()
plt.show()
2.3 效果呈现
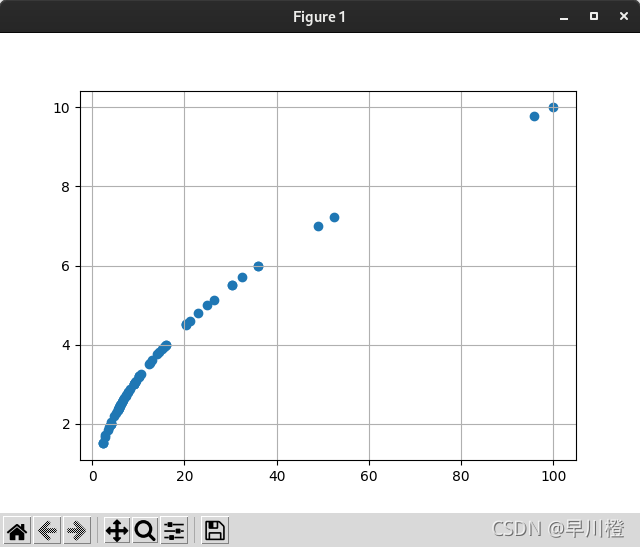
3、正态资料相关性分析
3.1 使用场景
待分析特征较多。可用它来分析正态分布的两个连续型变量之间的相关性,常用于分析自变量之间,以及自变量与因变量之间的相关性。
3.2 皮尔森相关系数
皮尔森相关系数是反应两个变量之间线性相关程度的统计量。
3.3 代码实现
import numpy as npa = np.random.normal(0,1,100)
b = np.random.normal(2,2,100)
print(stats.pearsonr(a,b))
3.4 结果分析
#(0.10245068885435506, 0.3104404938078574)
- ret1:相关系数,其取值范围为[-1,1]。其值接近于1,正相关正读越强,接近于-1,负相关性越强,接近于0,相关性弱。
- ret2:p-value:皮尔森相关系数原假设为两组数据不存在相关性。p-value >0.05 接受原假设。
4、非正太资料的相关分析
4.1 使用场景
待分析特征较多,只考虑从变量值的顺序(rank,秩或称等级),而不考虑变量值的大小,常用于计算有序的类型变量的相关性。可以用于非正太变量的相关性检验,但是它只考虑数据大小的顺序,而不考虑具体的值,导致会丢失部分信息。
4.2 斯皮尔曼等级相关系数
主要用于评价顺序变量间的线性相关关系。
4.3 代码实现
from scipy import stats
import numpy as npa = np.array([1,2,3,4,5])分析
b = np.array([1,6,7,8,20])
print(stats.spearmanr(a,b))
4.4 结果分析
SpearmanrResult(correlation=0.9999999999999999, pvalue=1.4042654220543672e-24)
- correlation:相关系数
- p-value:原假设为两组数据之间不存在相关性,p-value < 0.05 原假设