数据结构和算法

一、前置扫盲

1、数据结构分类

1.1 逻辑结构：线性与非线性

tip：逻辑结构揭示了数据元素之间的逻辑关系。

线性数据结构：元素间存在明确的顺序关系。
1. 数据按照一定顺序排列，其中元素之间存在一个对应关系，使得它们按照线性顺序排列。
2. 每个元素都有且仅有一个前驱元素和一个后继元素，除了第一个和最后一个元素外。
3. 代表：数组、链表、栈、队列、哈希表。
非线性数据结构：元素不是按照序列排列的
- 元素之间存在多对多的关系，其组织方式不受固定顺序的限制。
- 非线性数据结构中的元素不是按照序列排列的。
- 代表：树、堆、图、哈希表。

图例：

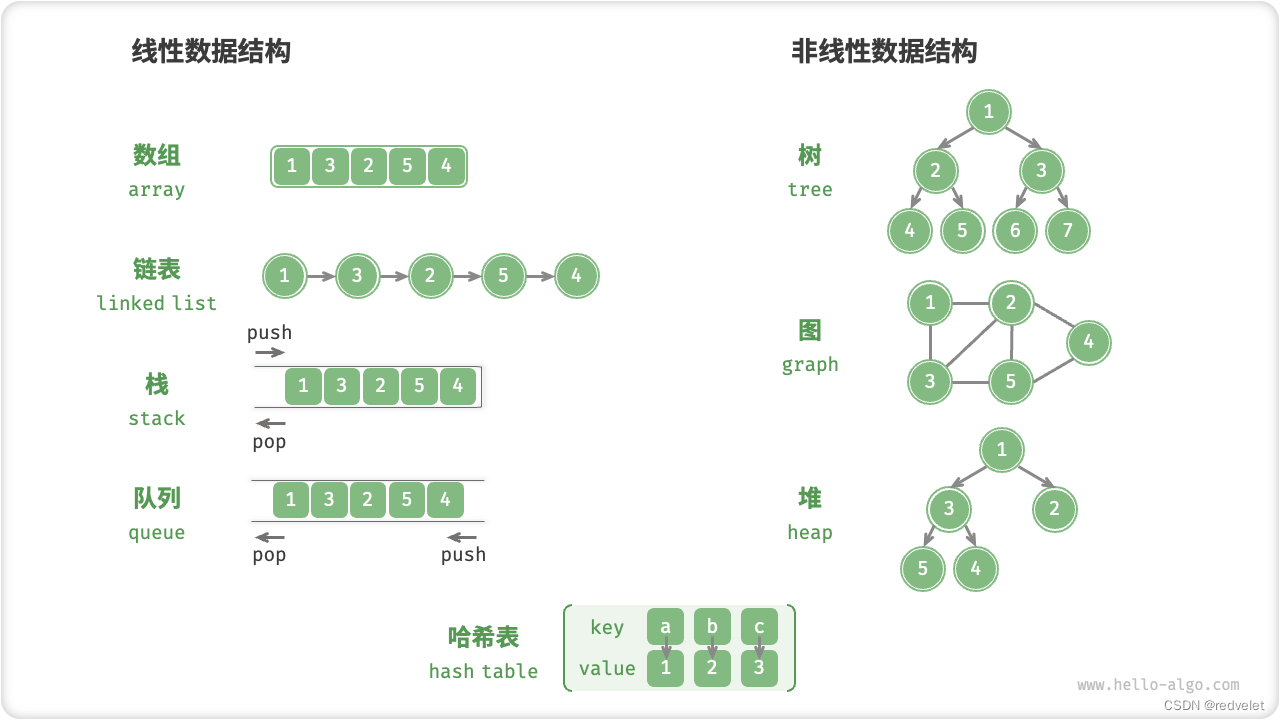
在这里插入图片描述

1.2 物理结构：顺序与链式

tip：所有数据结构都是基于数组、链表或二者的组合实现的

连续空间存储（顺序）：
1. 特点：数据元素存储在物理空间上是连续的，通过元素的物理地址和相对位置来访问数据。
2. 优缺点：
  - 优点： 随机访问速度快，存储效率高。
  - 缺点： 插入和删除操作可能涉及大量数据的移动，且需要预先分配连续的内存空间。
3. 代表：基于数组可实现：栈、队列、哈希表、树、堆、图、矩阵、张量（维度 ≥3 的数组）等。
分散空间存储（链式）：
1. 特点：数据元素存储在物理空间上是分散的，通过指针来连接各个元素。
2. 优缺点：
  - 优点： 插入和删除操作相对容易，不需要连续的内存空间。
  - 缺点： 不支持快速的随机访问，需要遍历才能找到特定位置的元素。
3. 代表：基于链表可实现：栈、队列、哈希表、树、堆、图等。

图例：

在这里插入图片描述

2、算法效率评估

tip：算法的效率主要评估的是时间和空间，名词称为-时间复杂度和空间复杂度，但是不是统计具体的算法运行时间和使用空间，而是统计算法运行时间和使用空间随着数据量变大时的增长趋势，使用大O计数法表示。

2.1 时间复杂度

例子：下列一段代码，分别使用两种方式统计时间复杂度。

void algorithm(int n) {int a = 2;  a = a + 1;  a = a * 2;  for (int i = 0; i < n; i++) {  System.out.println(0);     }
}

2.1.1 统计具体时间

确定运行平台，包括硬件配置、编程语言、系统环境等，这些因素都会影响代码的运行效率。
评估各种计算操作所需的运行时间，假如加法操作 + 需要 1 ns ，乘法操作 * 需要 10 ns ，打印操作 print() 需要 5 ns 等。
统计代码中所有的计算操作，并将所有操作的执行时间求和，从而得到运行时间。

// 在某运行平台下
void algorithm(int n) {int a = 2;  // 1 nsa = a + 1;  // 1 nsa = a * 2;  // 10 ns// 循环 n 次for (int i = 0; i < n; i++) {  // 1 ns ，每轮都要执行 i++System.out.println(0);     // 5 ns}
}

根据以上方法，可以得到算法的运行时间为 (6n+12) ns 。

统计算法的运行时间既不合理也不现实。

预估时间和运行平台绑定，因为算法需要在各种不同的平台上运行。
很难获知每种操作的运行时间，这给预估过程带来了极大的难度。

2.1.2 统计增长趋势

“时间增长趋势(是算法运行时间随着数据量变大时的增长趋势)”这个概念比较抽象，我们通过一个例子来加以理解。假设输入数据大小为 n ，给定三个算法 A、B 和 C ：

// 算法 A 的时间复杂度：常数阶
void algorithm_A(int n) {System.out.println(0);
}
// 算法 B 的时间复杂度：线性阶
void algorithm_B(int n) {for (int i = 0; i < n; i++) {System.out.println(0);}
}
// 算法 C 的时间复杂度：常数阶
void algorithm_C(int n) {for (int i = 0; i < 1000000; i++) {System.out.println(0);}
}

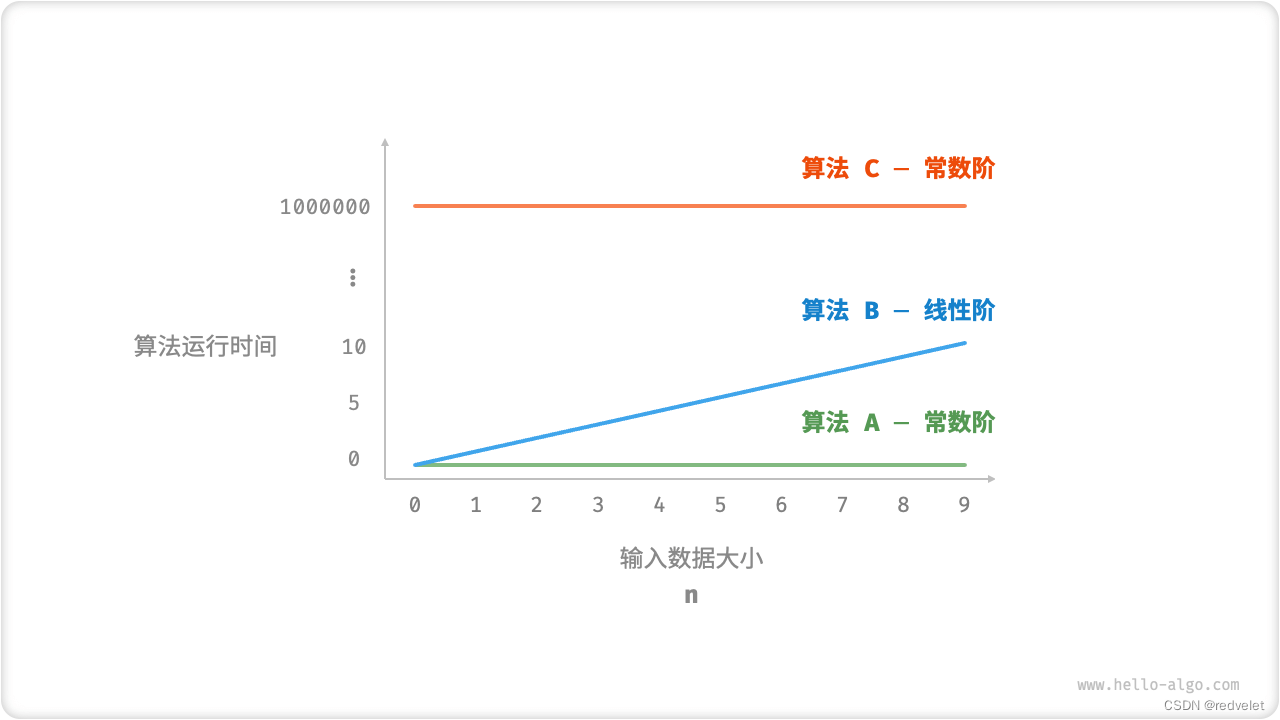
在这里插入图片描述

算法 A 只有 1 个打印操作，算法运行时间不随着 n增大而增长。我们称此算法的时间复杂度为“常数阶”。
算法 B 中的打印操作需要循环 n 次，算法运行时间随着 n 增大呈线性增长。此算法的时间复杂度被称为“线性阶”。
算法 C 中的打印操作需要循环 1000000 次，虽然运行时间很长，但它与输入数据大小n 无关。因此 C 的时间复杂度和 A 相同，仍为“常数阶”

相较于直接统计算法的运行时间，时间复杂度的特点：

时间复杂度能够有效评估算法效率。例如，算法 B 的运行时间呈线性增长，在 n>1 时比算法 A 更慢，在n>1000000时比算法 C 更慢。事实上，只要输入数据大小 n 足够大，复杂度为“常数阶”的算法一定优于“线性阶”的算法，这正是时间增长趋势的含义。
时间复杂度的推算方法更简便。显然，运行平台和计算操作类型都与算法运行时间的增长趋势无关。因此在时间复杂度分析中，我们可以简单地将所有计算操作的执行时间视为相同的“单位时间”，从而将“计算操作运行时间统计”简化为“计算操作数量统计”，这样一来估算难度就大大降低了。
时间复杂度也存在一定的局限性。例如，尽管算法 A 和 C 的时间复杂度相同，但实际运行时间差别很大。同样，尽管算法 B 的时间复杂度比 C 高，但在输入数据大小 n 较小时，算法 B 明显优于算法 C 。在这些情况下，我们很难仅凭时间复杂度判断算法效率的高低。当然，尽管存在上述问题，复杂度分析仍然是评判算法效率最有效且常用的方法。

具体计算方式：使用函数T(n)演变为O(n)表示。

void algorithm(int n) {//每次调用函数执行的次数int a = 1;  // +1a = a + 1;  // +1a = a * 2;  // +1// 循环 n 次for (int i = 0; i < n; i++) { // +1（每轮都执行 i ++）System.out.println(0);    // +1}
}

设算法的操作数量是一个关于输入数据大小 n 的函数，记为T(n)，则以上函数的操作数量为
$T (n) = 3 + 2 n$
T(n)是一次函数，说明其运行时间的增长趋势是线性的，因此它的时间复杂度是线性阶，我们将线性阶的时间复杂度记为O(n)，这个数学符号称为「大O记号big-O notationJ,表示函数T(n)的「渐近上界asymptotic upper bound」。

代码的时间复杂度：线性阶时间复杂度
函数表示：T(n)=3+2n
线性阶表示：O(3+2n)
- 输入的n不受控制，可以为任意数，而时间复杂度是很难计算准确的，所以统计的为最差情况的时间复杂度。
- 假如输入n的数趋近于∞（无穷），那么常数3可以忽略，同理系数2也可以忽略，无穷和2倍无穷不还是无穷吗
- 所以最终时间复杂度表示为：O(n)

总结：

计数简化技巧：

忽略T(n) 中的常数项。因为它们都与 n 无关，所以对时间复杂度不产生影响。
省略所有系数。例如，循环 2n 次、5n+1 次等，都可以简化记为 n 次，因为 n前面的系数对时间复杂度没有影响。
循环嵌套时使用乘法。总操作数量等于外层循环和内层循环操作数量之积，每一层循环依然可以分别套用第 1. 点和第 2. 点的技巧。
最差情况判断：当输入数最差情况为n，趋近于无穷大时，最高阶的项将发挥主导作用，其他项的影响都可以忽略。

void algorithm(int n) {int a = 1;  // +1a = a + n;  // +1// +5nfor (int i = 0; i < 5 * n + 1; i++) {System.out.println(0);}// +2nfor (int i = 0; i < 2 * n; i++) {//加n+1for (int j = 0; j < n + 1; j++) {System.out.println(0);}}
}

$函数表示：T(n)=2+5n+2n(n+1)=2n^2+7n+3$

$大O计数法表示：O(n^2)---当n->∞,n^2为主导，除去常数、系数、非主导项，使用$

拓展：常见大O类型和图例

$时间复杂度：O(1) < O(logn)<O(n)<O(nlogn)<O(n^2)<O(2^n)<O(n!)$

$时间复杂度：常数阶 < 对数阶 < 线性阶 < 线性对数阶 < 平方阶 < 指数阶 < 阶层阶$

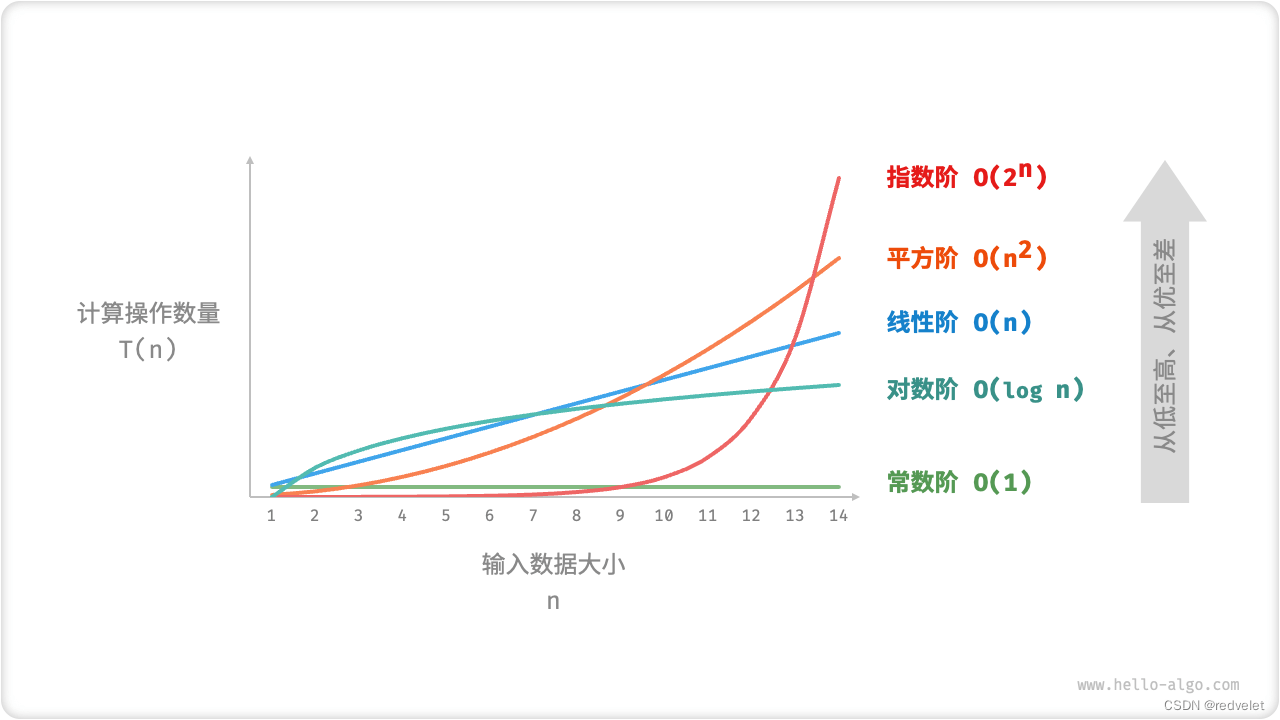
在这里插入图片描述

线性阶的操作数量相对于输入数据大小 n以线性级别增长。线性阶通常出现在单层循环中
平方阶的操作数量相对于输入数据大小 n 以平方级别增长。平方阶通常出现在嵌套循环中
生物学的“细胞分裂”是指数阶增长的典型例子：初始状态为 1 个细胞，分裂一轮后变为 2 个，分裂两轮后变为 4 个，以此类推，分裂 n 轮后有 2^n 个细胞，指数阶常出现于递归函数中。
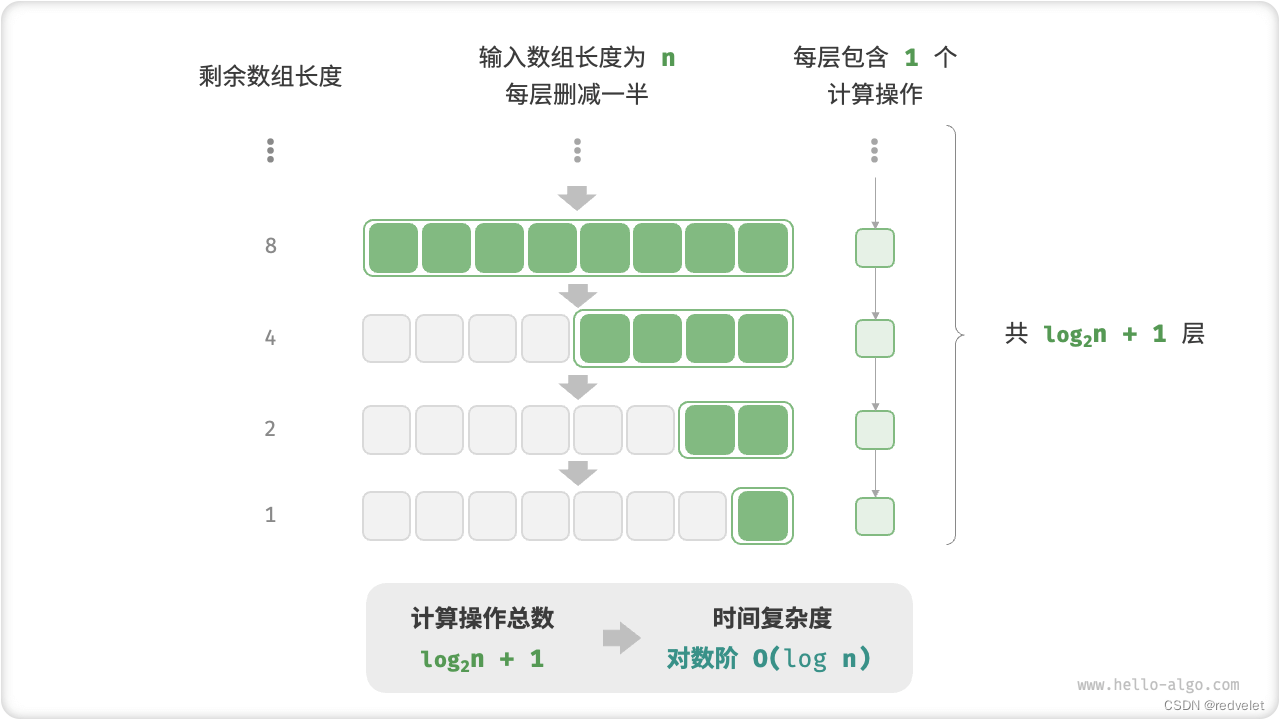
对数阶反映了“每轮缩减到一半”的情况。设输入数据大小为 n ，由于每轮缩减到一半，因此循环次数是 log2⁡n ，即 2^n 的反函数。
线性对数阶常出现于嵌套循环中
阶乘阶对应数学上的“全排列”问题。给定 n 个互不重复的元素，求其所有可能的排列方案，方案数量为n!，常用于回溯。