1 高斯分布数学表达
1.1 什么是高斯分布
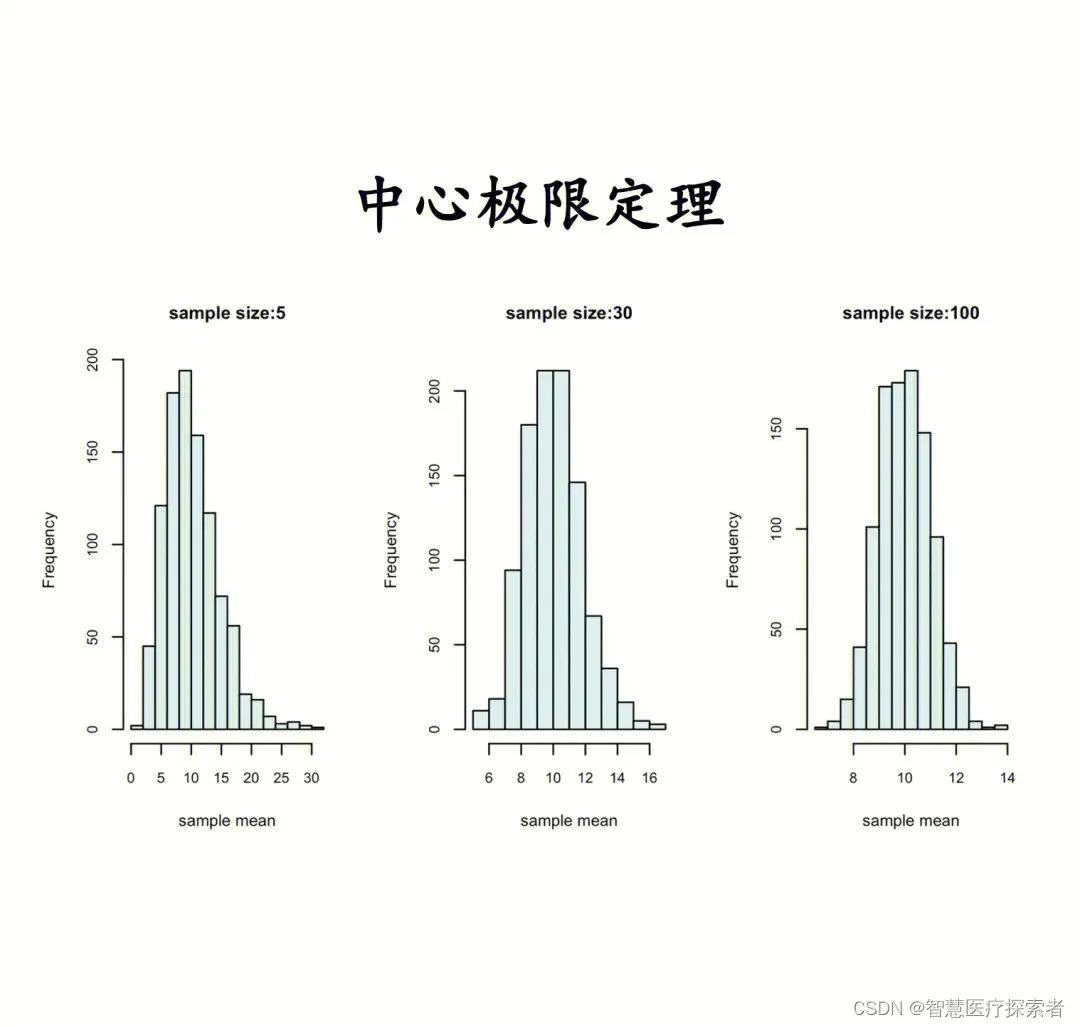
高斯分布(Gaussian Distribution)又称正态分布(Normal Distribution)。高斯分布是一种重要的模型,其广泛应用与连续型随机变量的分布中,在数据分析领域中高斯分布占有重要地位。高斯分布是一个非常常见的连续概率分布。由于中心极限定理(Central Limit Theorem)的广泛应用,高斯分布在统计学上非常重要。中心极限定理表明,由一组独立同分布,并且具有有限的数学期望和方差的随机变量X1,X2,X3,...Xn构成的平均随机变量Y近似的服从正态分布当n趋近于无穷。另外众多物理计量是由许多独立随机过程的和构成,因而往往也具有高斯分布。
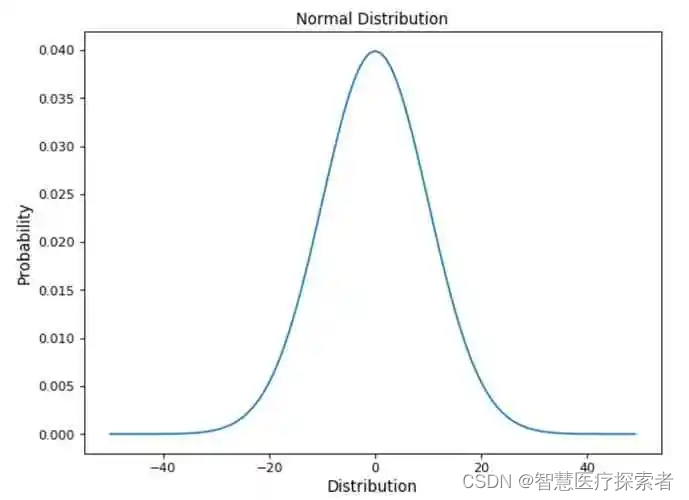
高斯分布的概率密度函数曲线呈钟形,因此又经常称之为钟形曲线。即随机变量X服从一个为数学期望μ、方差为σ^2的高斯分布,记为N(μ,σ^2)。在高斯分布中,以数学期望μ表示钟型的中心位置(也即曲线的位置),而标准差(standard deviation)σ表征曲线的离散程度。
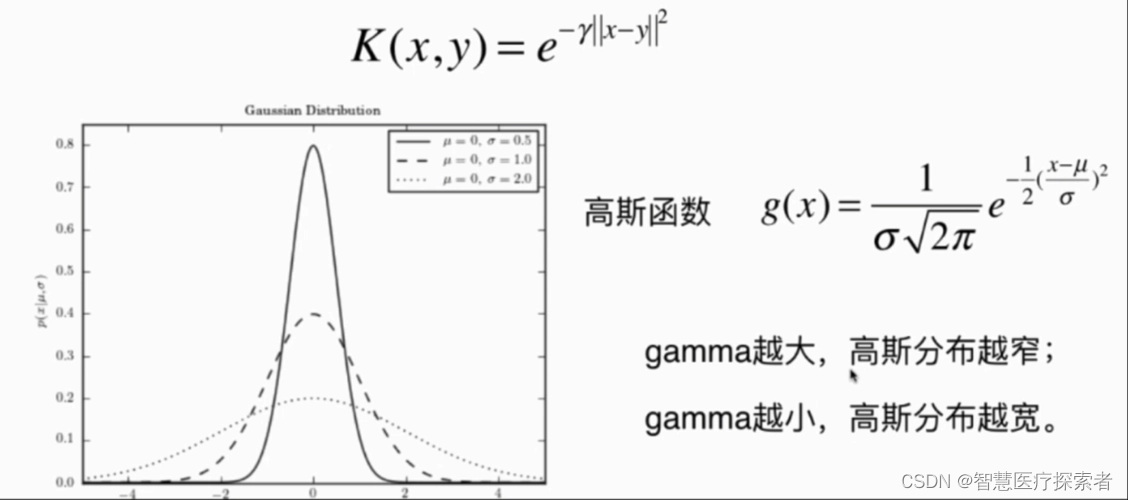
当数学期望为0(u=0),方差为1(σ=1)时,该分布为标准正态分布(standard normal distribution)。下图展示了几种不同类型的正态分布概率密度函数曲线。
1.2 关键概念
-
概率函数:把事件概率表示成关于事件变量的函数
-
概率分布函数:一个随机变量ξ取值小于某一数值x的概率,这概率是x的函数,称这种函数为随机变量ξ的分布函数,简称分布函数,记作F(x),即F(x)=P(ξ<x) (-∞<x<+∞),由它并可以决定随机变量落入任何范围内的概率。
-
概率密度函数:
概率密度等于变量在一个区间(事件的取值范围)的总的概率除以该段区间的长度。
概率密度函数是一个描述随机变量在某个确定的取值点附近的可能性的函数。
1.3 一元高斯分布
若随机变量X服从均值为μ,方差为σ2的高斯分布,那么:

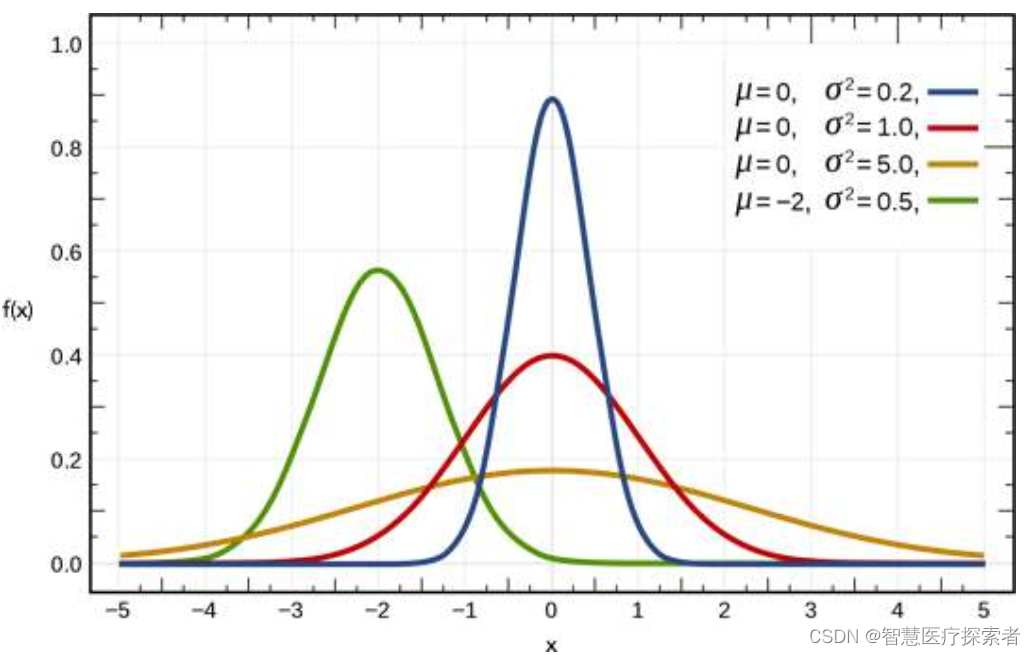
高斯分布的图形像钟一样,下图展示了一般正态分布的图形。其中 μ = 0 , σ = 1。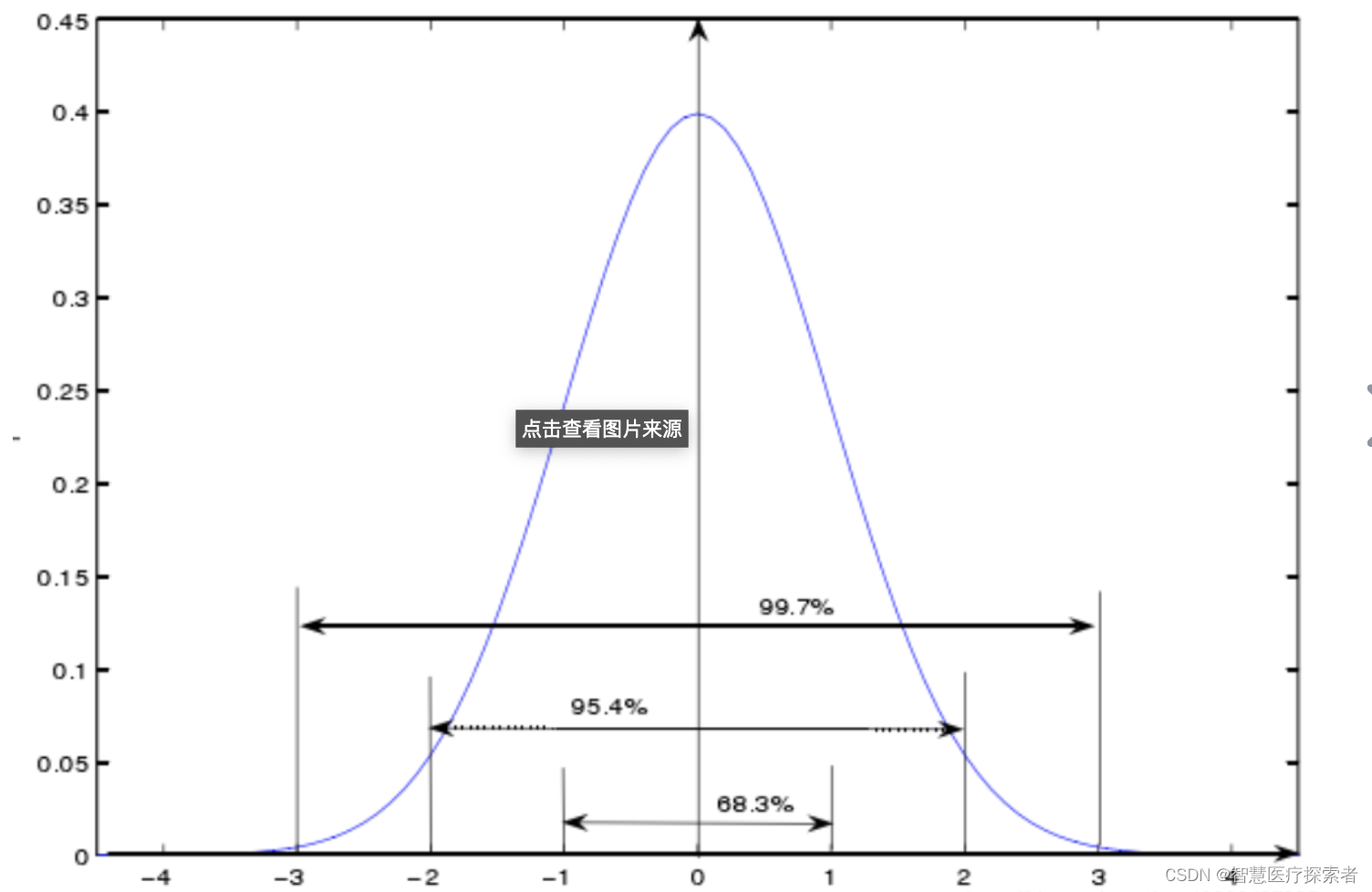
对于一个非标准的正态分布,可以由标准正态分布经过以下3步变换得到:
-
将x向右移动u个单位
-
将密度函数x轴延展sigma倍
-
将函数密度图像y轴压缩σ倍
如果X服从分布,X ∼ N(μ, σ2),那么具有以下的性质:

1.4 多元高斯分布
1.4.1 独立多元高斯分布

如果我们令:
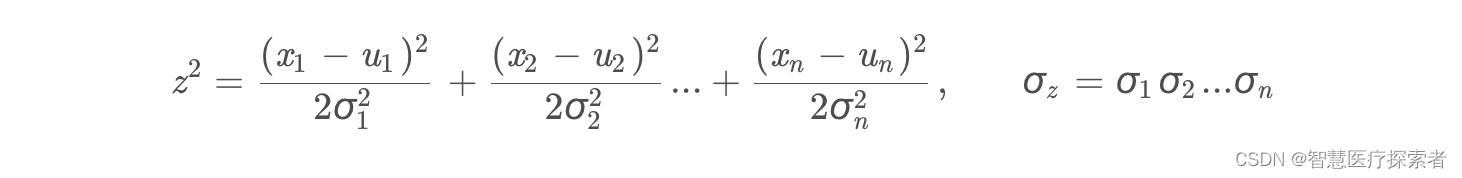
我们有:
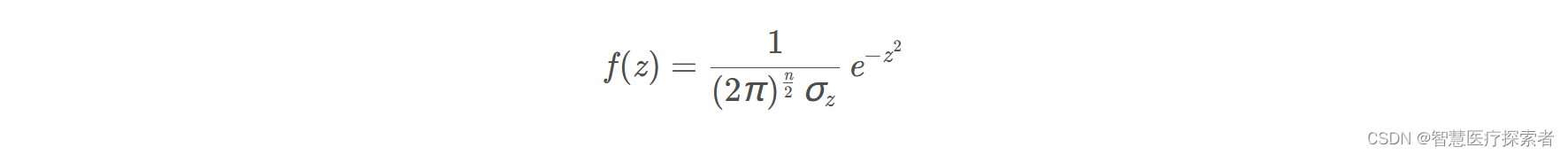
使用矩阵的形式来表示的话,则有:
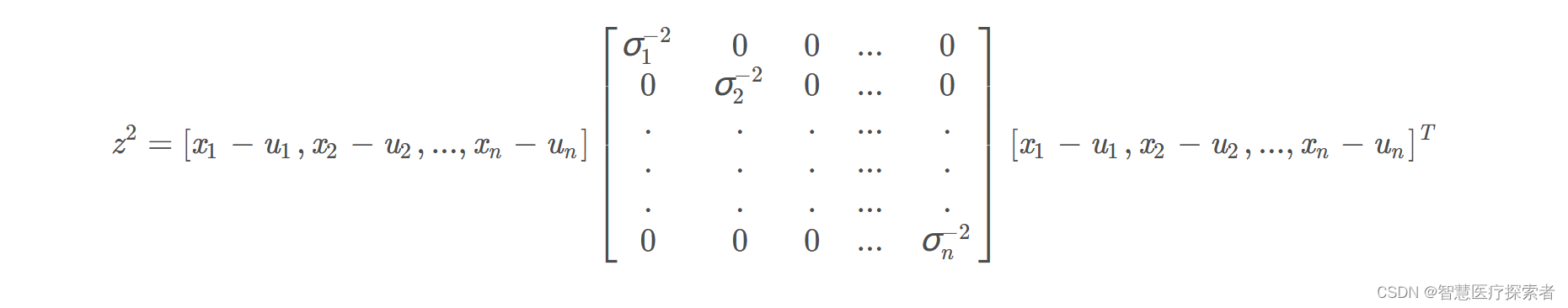
定义符号:
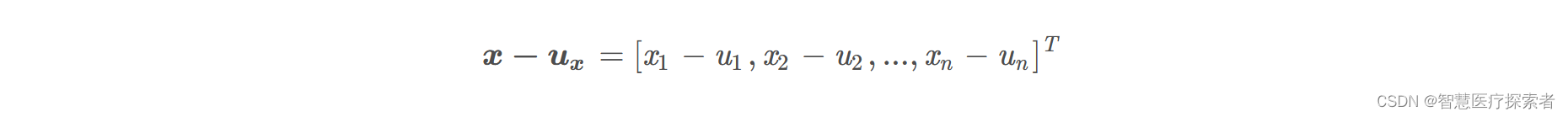
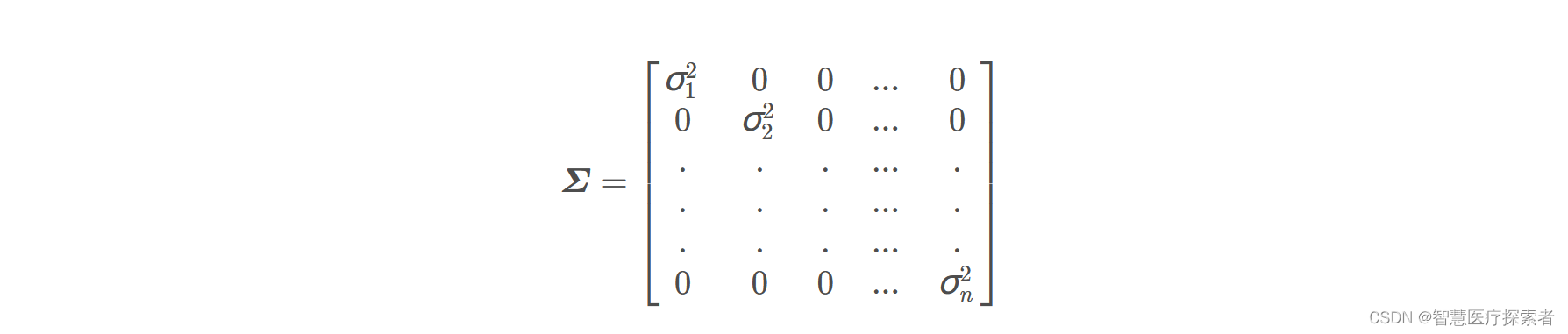
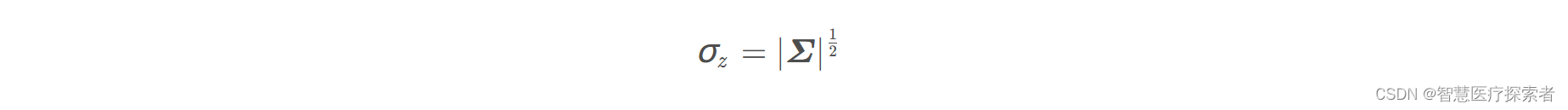
变量代换可得:
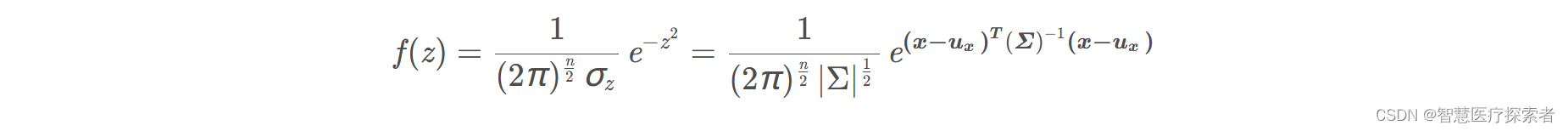
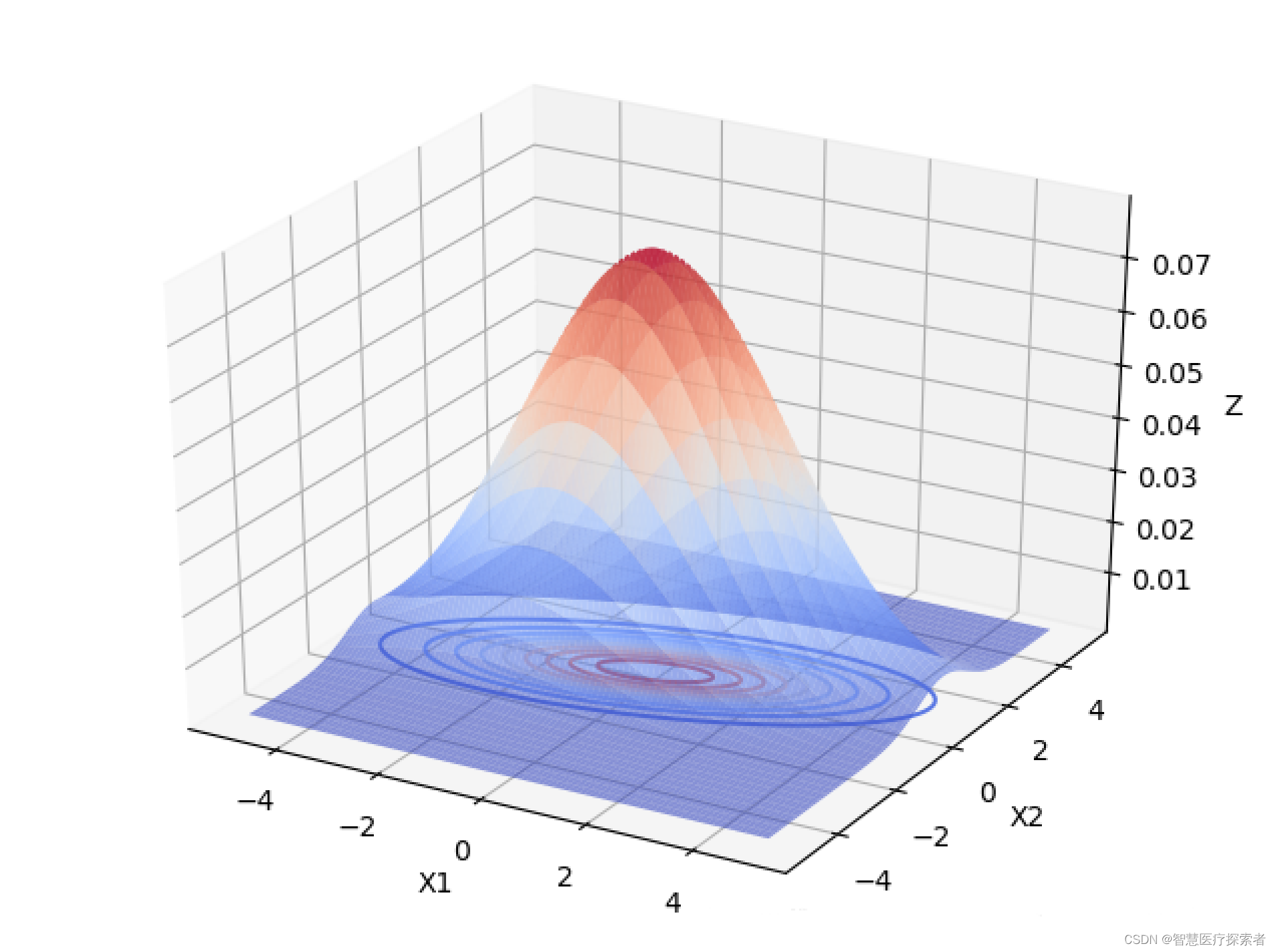
下面以 为例,画出二元高斯分布在变量之间相互独立的图像:

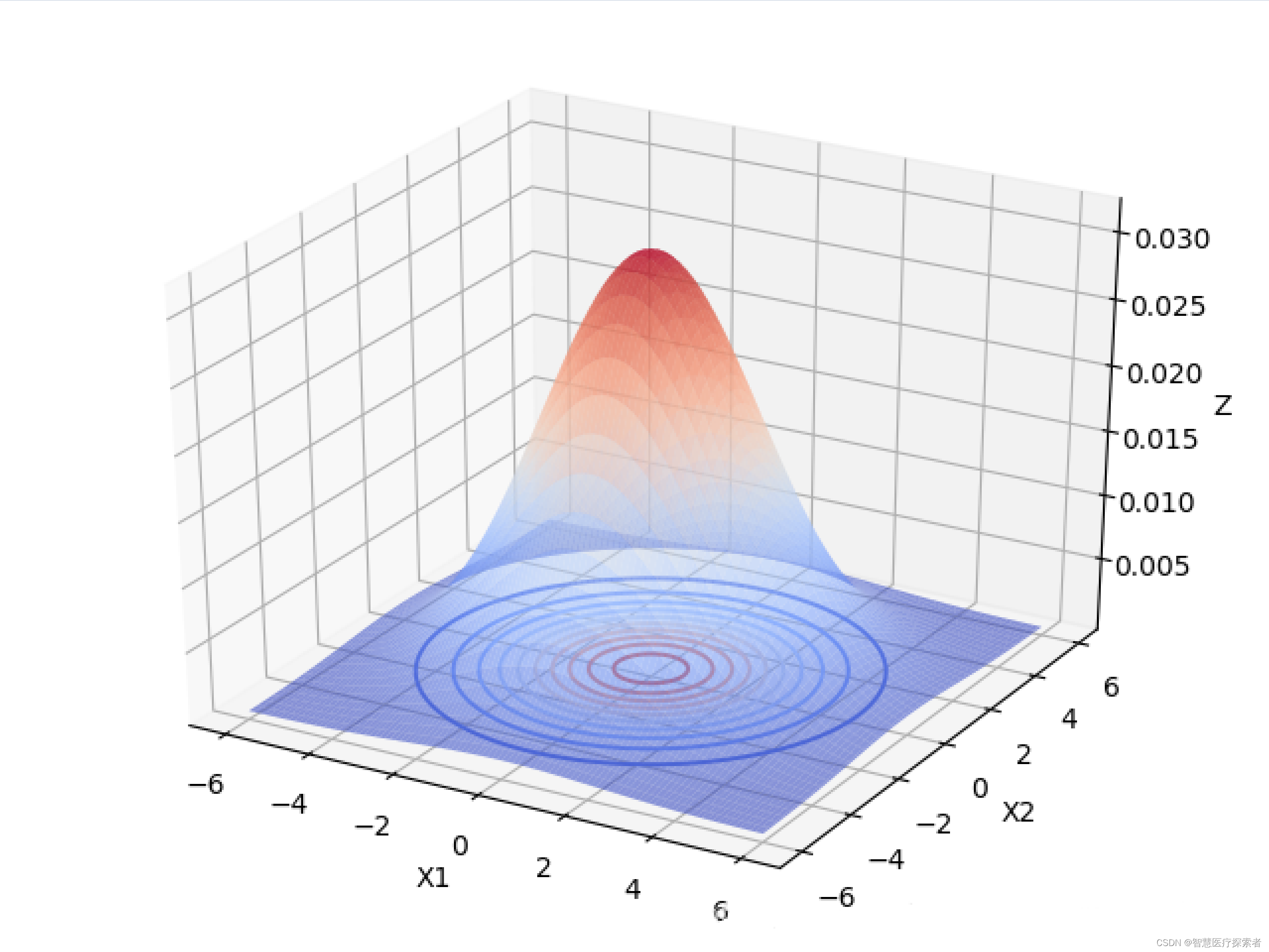

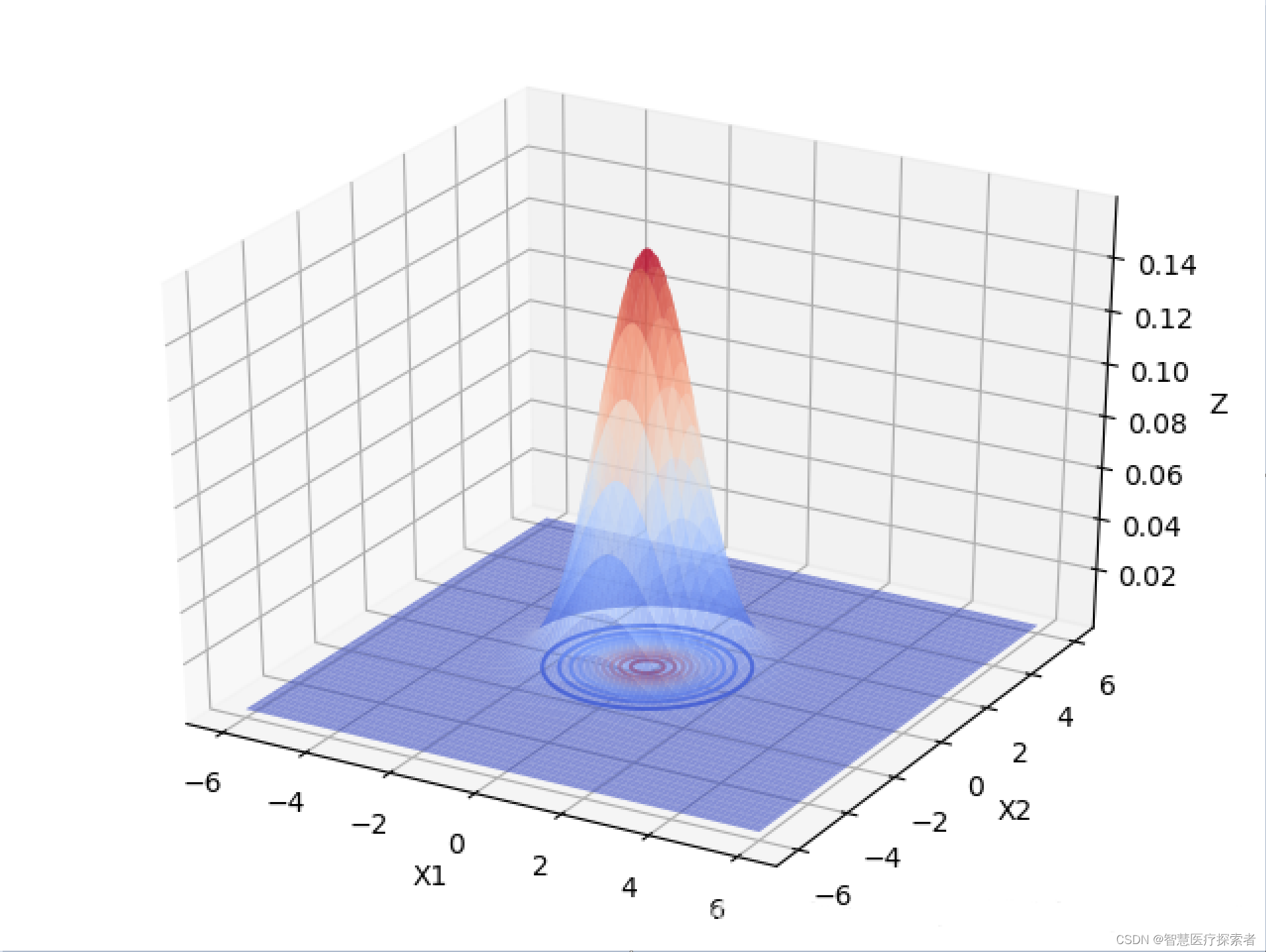

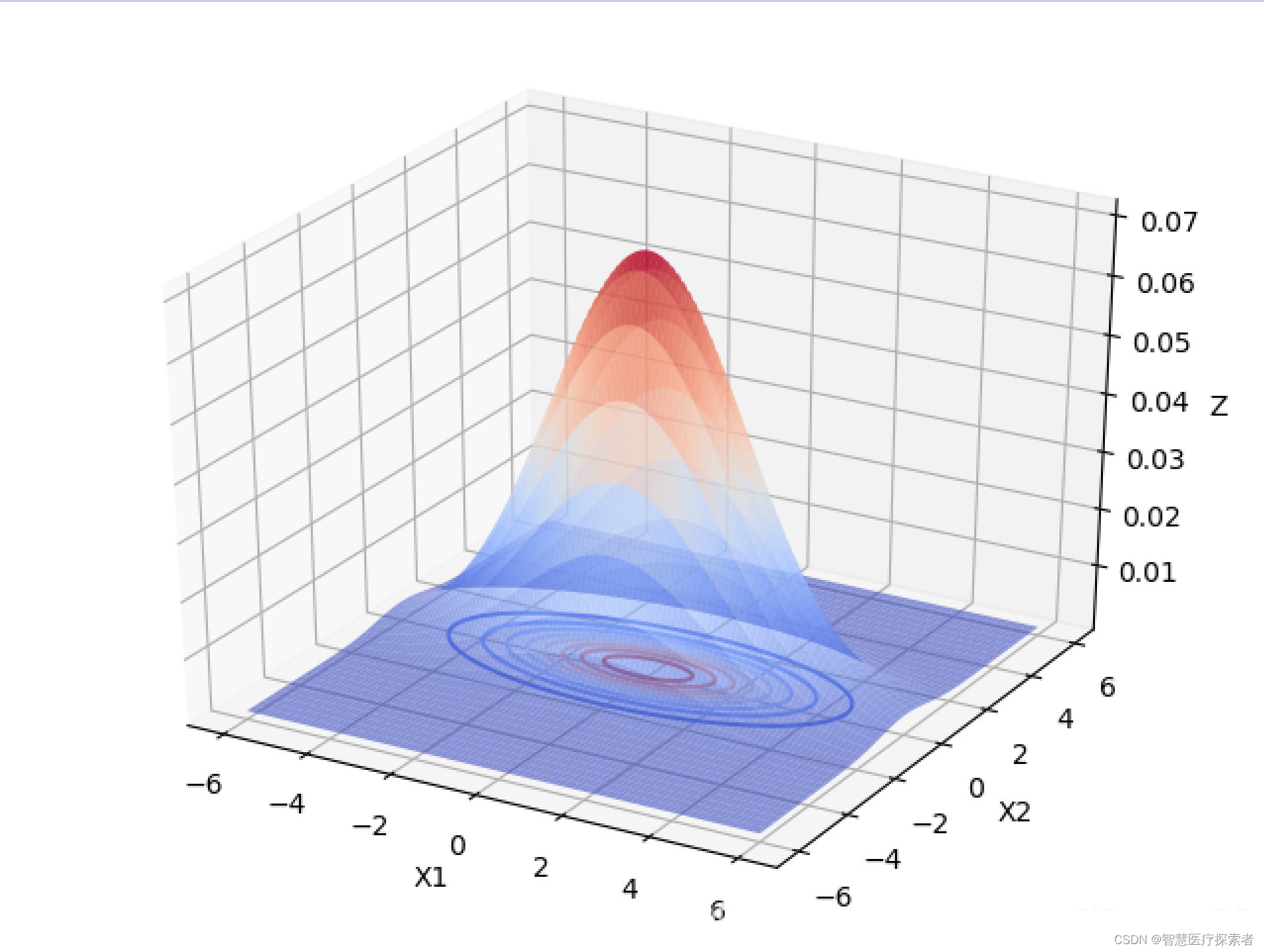

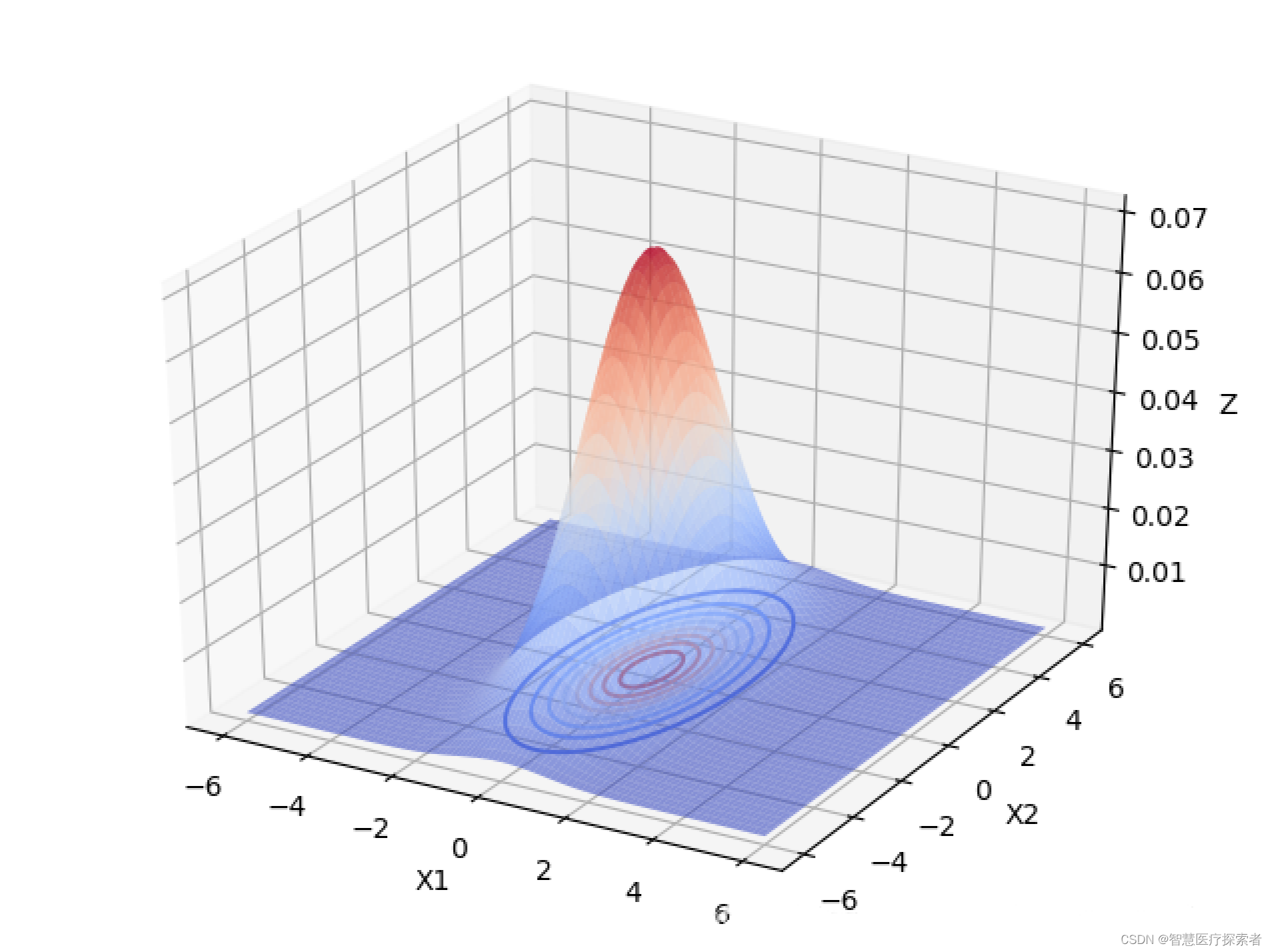
由上图可以看出,当变量之间相互独立的时候:
-
当协方差矩阵的特征值越小时,分布函数图像越高越尖。
-
当协方差矩阵的特征值相等时,分布函数图像在X1,X2面上的投影是圆形的。当特征值不相等时,分布函数图像在X1,X2面上的投影是椭圆形的,X1,X2相互独立时,椭圆的长轴和短轴平行与坐标轴。且变量对应的特征值越大,该变量分布的范围越分散,在二元高斯分布中,对应特征值大的变量在函数投影图像中对应的是椭圆的长轴。高维的高斯分布情况可以按照这个规律进行推广。
1.4.2 多元相关变量高斯分布
当变量之间存在相关关系的时候,协方差矩阵不再是对角阵,而是一个对称的矩阵,矩阵的每个元素表示变量
的协方差。


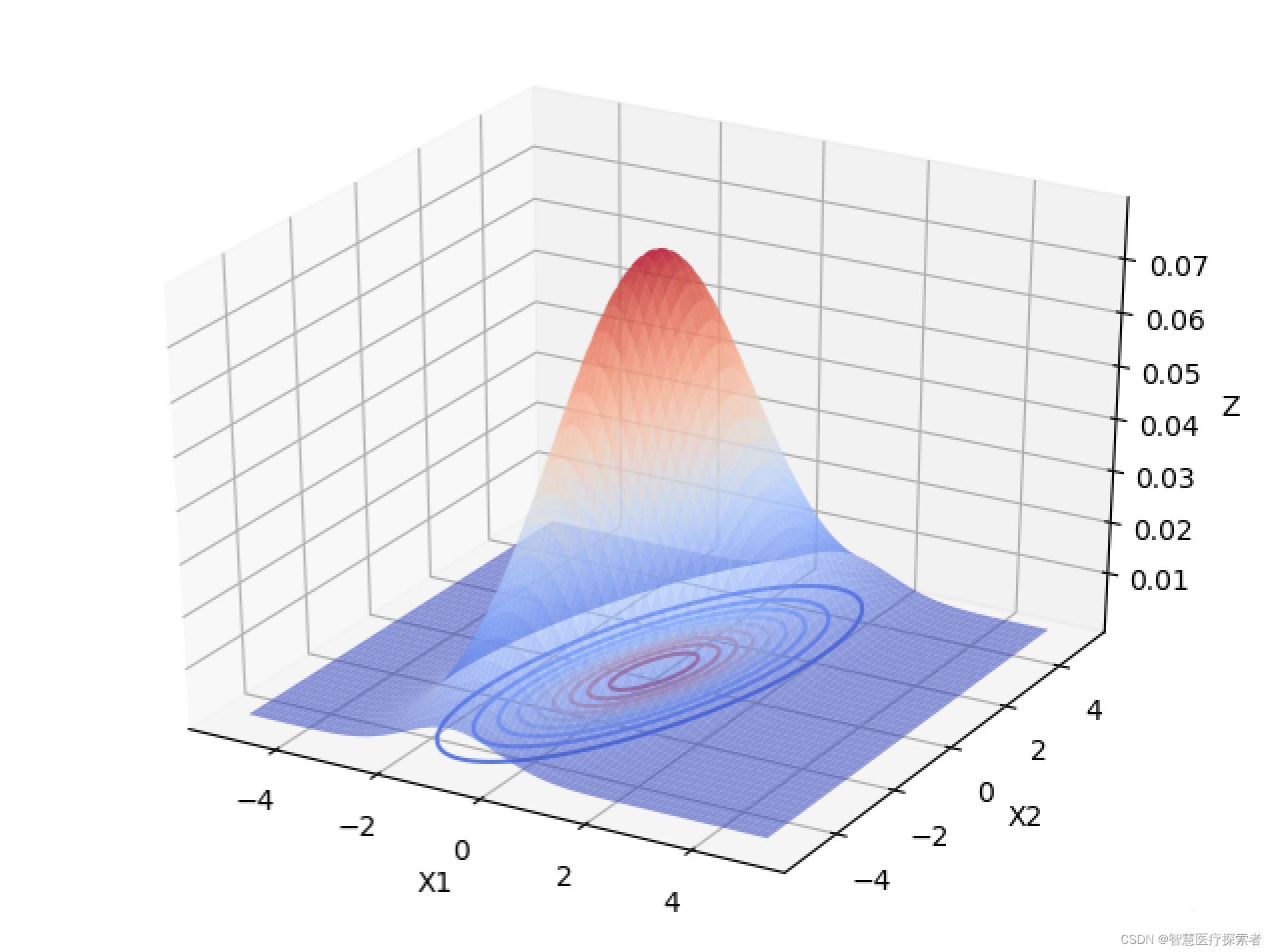
从上面2个图像中可以看出,变量之间具有相关关系时,与变量之间相互独立最大的区别是,投影面的椭圆长短轴不再平行与坐标轴。如果我们将坐标轴X1,X2旋转一下,与椭圆的长短轴平行,如下图所示:
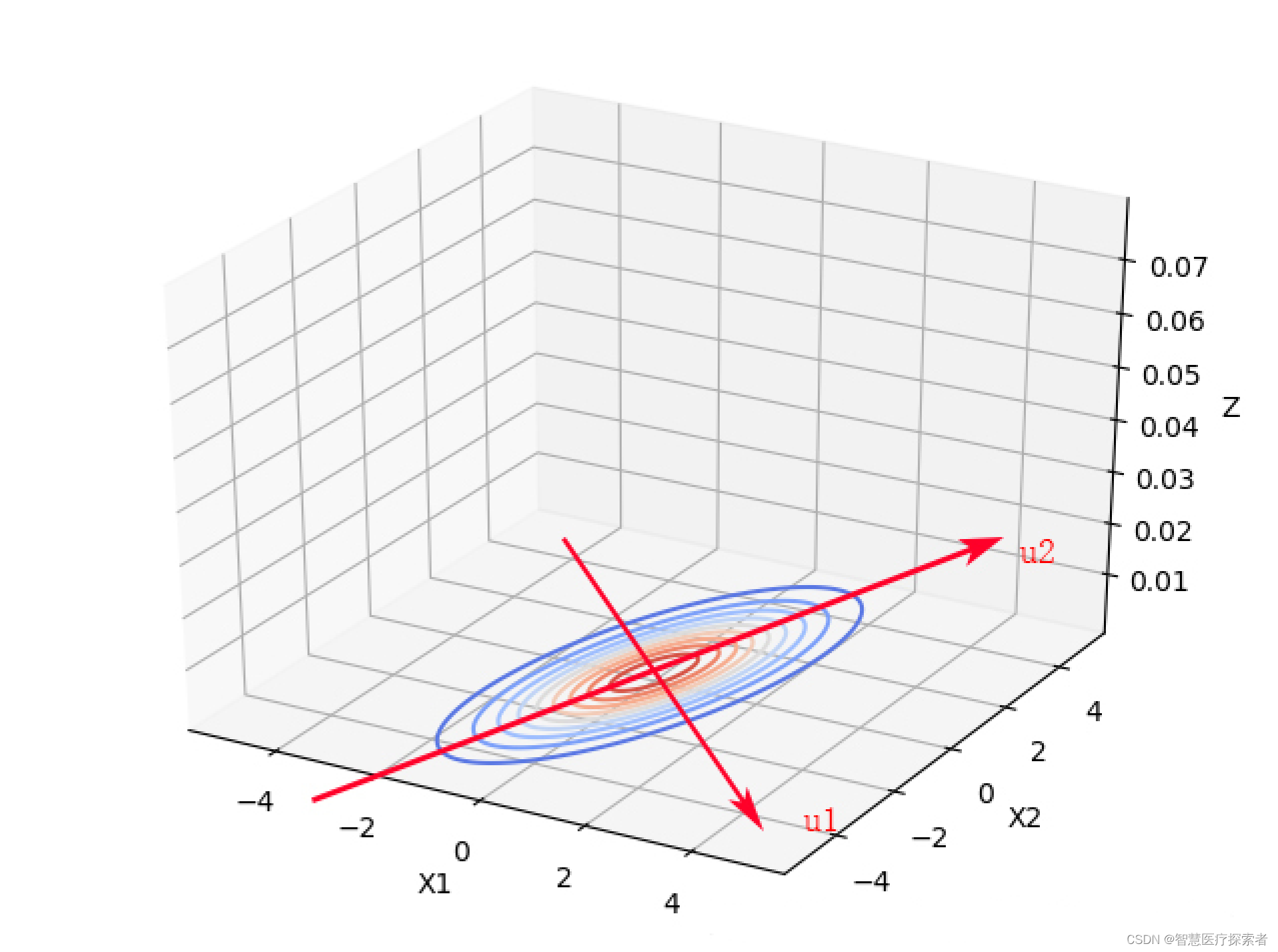
由独立变量的二元高斯分布知,那么在新的坐标系下, 是相互独立的。上述过程称作为去相关性,这也是经典的降维方法主成分分析PCA的基础。以下是新坐标系的求解和原坐标系上的点在新坐标系下的坐标数学表达。
根据协方差矩阵的特征方程求解协方差矩阵的单位正交特征向量(先求出特征向量,再进行正交化与单位化),


此时之间没有相关关系。
2 高斯分布在深度学习中的作用
2.1 高斯分布广泛使用的原因
高斯分布(也称为正态分布或钟形曲线)在深度学习中被广泛应用的原因有以下几个方面:
-
中心极限定理:高斯分布具有重要的数学性质,其中最重要的是中心极限定理。该定理指出,对于大多数随机变量的和,其分布趋向于高斯分布。这意味着在实际问题中,许多现象可以通过高斯分布来近似描述。
-
参数化灵活性:高斯分布具有两个重要参数,均值和标准差,可以通过这两个参数来灵活地调整分布的形状。这使得高斯分布能够适应不同数据集的特征,并具有较强的拟合能力。
-
中心性和离散性度量:高斯分布在数学上具有对称性,其均值和中位数相等,这使得它成为测量数据集中心性的一种常用方法。此外,标准差作为高斯分布的度量,能够衡量数据的离散程度。
-
最大似然估计:在概率统计中,最大似然估计是一种常用的参数估计方法。高斯分布的参数估计可以通过最大似然估计进行计算,这使得高斯分布的应用更为方便。
在实际意义上,高斯分布在自然界和社会现象中出现的频率很高。许多自然和社会现象具有随机性,并且可以用高斯分布来描述。例如,在测量误差、人口统计、金融市场波动等领域中,高斯分布都被广泛应用。
2.2 高斯分布的应用场景
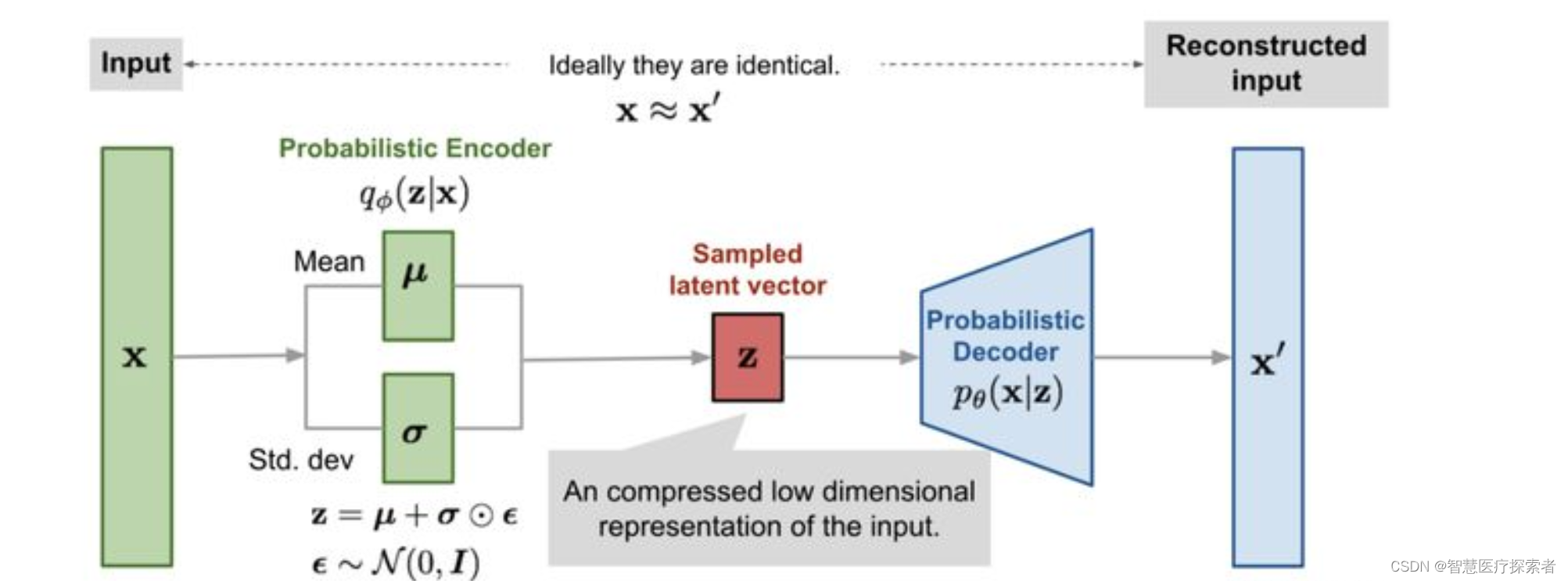
高斯分布(也称为正态分布)在深度学习模型中扮演着多个重要角色。以下是一些主要的应用场景:
-
参数初始化:在神经网络的训练开始时,通常需要对权重进行初始化。使用高斯分布(尤其是标准正态分布)来初始化权重可以帮助在训练初期避免激活函数的饱和,确保初始权重既不太大也不太小。
-
正则化:在某些情况下,高斯分布被用作先验分布,加入到损失函数中作为正则化项。这种正则化(如 L2 正则化)可以帮助防止过拟合,通过对权重的大小进行约束。
-
生成模型:在生成对抗网络(GANs)和变分自编码器(VAEs)等生成模型中,高斯分布常用于生成潜在空间中的随机噪声。这些噪声向量后续被用来生成数据(如图像)。
-
概率建模:在许多概率深度学习模型中,高斯分布用于建模输出变量,尤其是在处理连续值(如回归问题)时。
-
激活函数:尽管不太常见,但在某些特殊的网络结构中,可以使用高斯函数作为激活函数,以模拟特定的生物神经网络行为。
-
不确定性估计:在贝叶斯神经网络中,权重和偏置被视为随机变量,通常使用高斯分布来描述它们的不确定性。这种方法可以提供模型预测的不确定性估计。
-
特征提取:在某些图像处理技术中,例如高斯模糊,使用高斯分布作为权重核,可以帮助模型在训练过程中更好地提取图像特征。
高斯分布由于其数学属性和在自然界中的普遍性,成为深度学习中的一个重要工具。它在处理不确定性、正则化和概率建模方面尤为重要。