目录

前言

一、绘制散点图

二、数据准备

三、一元线性回归模型训练

四、一元线性回归模型评估

总结

---

🌈嗨！我是Filotimo__🌈。很高兴与大家相识，希望我的博客能对你有所帮助。

💡本文由Filotimo__✍️原创，首发于CSDN📚。

📣如需转载，请事先与我联系以获得授权⚠️。

🎁欢迎大家给我点赞👍、收藏⭐️，并在留言区📝与我互动，这些都是我前进的动力！

🌟我的格言：森林草木都有自己认为对的角度🌟。

前言

机器学习中的一元线性回归问题是指预测一个因变量（响应变量）和一个自变量（特征变量）之间的线性关系。具体地说，给定一个包含自变量和因变量的数据集，我们可以通过训练一个线性回归模型来学习这种关系，并利用该模型来进行预测或者推断。

在这里，我们简单介绍一下在一元线性回归中的一些关键术语和流程：

特征：在一元线性回归中，我们只有一个特征（或自变量），它是用来预测因变量的变量。
标签：标签是我们的目标输出（或因变量），它是由模型来预测的值。
模型：模型就是训练过程中学到的函数，它将给定的自变量映射到因变量的预测值。
训练集：训练集是用来训练模型的数据集。我们通过输入自变量 x 的值和对应的因变量 y 值来训练（拟合）用于学习的模型。
测试集：测试集是用来测试模型预测准确度的数据集。我们在测试集上输入自变量 x 的值，然后通过模型预测其对应的因变量 y 值，并将其与测试集中真实的因变量 y 值进行比较。
均方误差（MSE）：MSE 是在评估回归问题模型性能时常用的指标之一，它是预测值与实际值之间差异的平方的均值。
决定系数（R2）：决定系数是一个用来衡量模型对数据的拟合程度好坏的指标，它的值介于 0 和 1 之间。R2 越接近 1，表示模型对数据的拟合程度越好，反之则越差。

---

一、绘制散点图

import matplotlib.pyplot as plt
from pylab import mpl   # 设置显示中文字体
mpl.rcParams["font.sans-serif"] = ["SimHei"]   # 设置正常显示符号
mpl.rcParams["axes.unicode_minus"] = False

mpl.rcParams 是一个全局配置字典，用于设置 matplotlib 的默认参数。我们将字体设置为 SimHei，以支持显示中文字体，并且设置 axes.unicode_minus 为 False，以解决负号显示的问题。

# 0.准备数据
x = [225.98,247.07,253.14,457.85,241.58,301.01,20.67,288.64,163.56,120.06,207.83,342.75,147.9,53.06,224.72,29.51,21.61,483.21,245.25,399.25,343.35]
y = [196.63,203.88,210.75,372.74,202.41,247.61,24.9,239.34,140.32,104.15,176.84,288.23,128.79,49.64,191.74,33.1,30.74,400.02,205.35,330.64,283.45]
# 1.创建画布
plt.figure(figsize=(20, 8), dpi=100)
# 2绘制图像
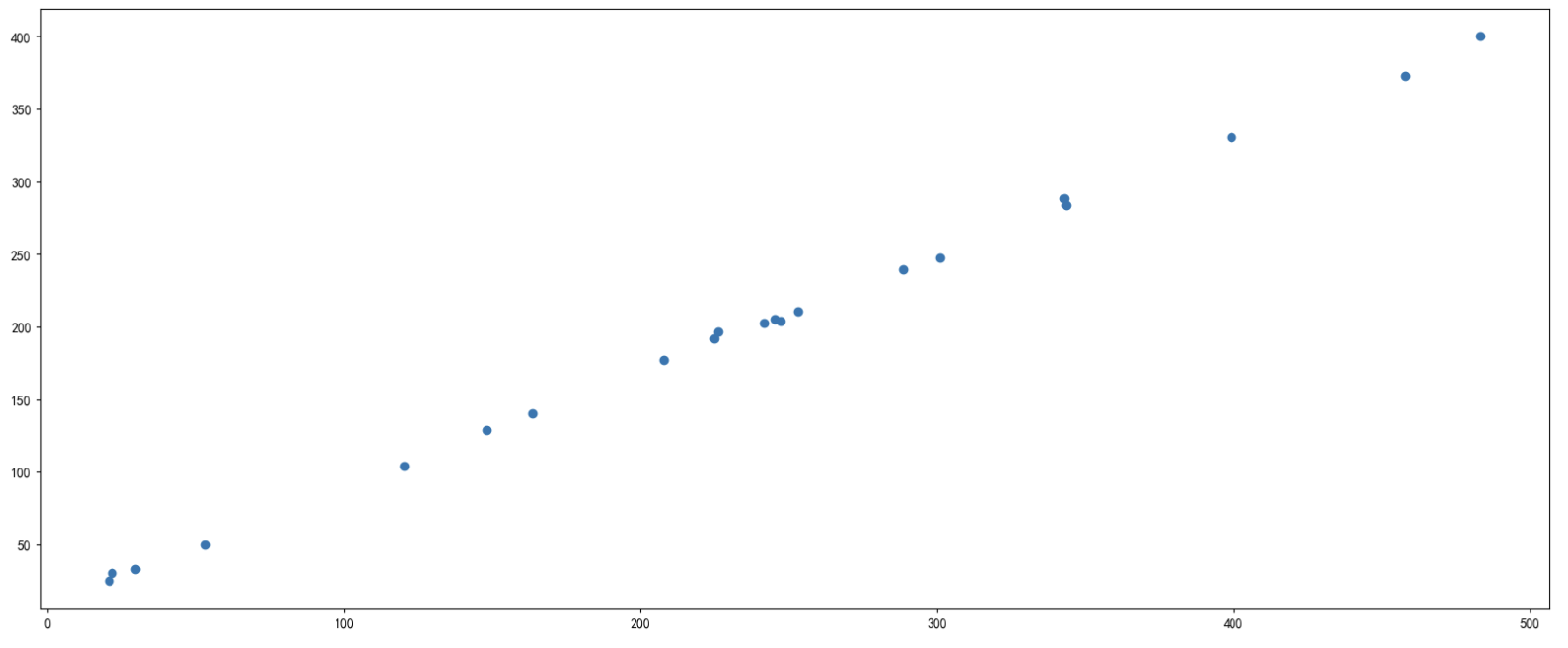
plt.scatter(x, y)
# 3.图像显示
plt.show()

我们定义了两个列表 x 和 y，用来存储披萨的价格 x 和销量 y 的数据。接着使用 matplotlib 库来创建一个大小为 20*8，dpi 为 100 的画布，并使用 scatter 函数在画布上绘制 x 和 y 的散点图。

x=[1, 2, 3, 4, 5]
y=[1, 3, 7, 8, 11]
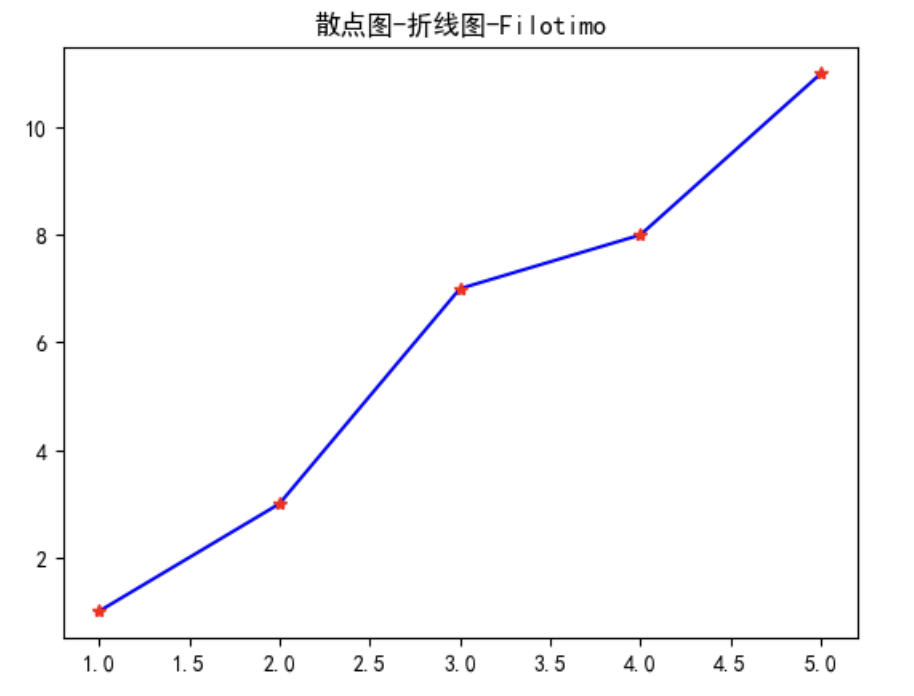
plt.title(u"散点图-折线图-Filotimo")
plt.plot(x, y, "b-")    # 绘制蓝色折线
plt.plot(x, y, "r*")    # 绘制红色星形散点图
plt.show()

在这段代码中，我们重新定义了新的 x 和 y 列表，然后使用 plot 函数在画布上绘制了散点图和折线图。

二、数据准备

X_train = [[6], [8], [10], [14], [18]] # 披萨直径
y_train = [[7], [9], [13], [17.5], [18]] # 披萨价格

我们定义了训练数据集 X_train 和 y_train，用来表示不同直径的披萨对应的价格。X_train 包含了披萨的直径，而 y_train 包含了给定直径的披萨价格。

plt.figure()
plt.plot(X_train, y_train, 'r*', markersize=10)
plt.title('披萨直径与价格的散点图')
plt.xlabel('直径(英寸)')
plt.ylabel('价格(美元)')
plt.axis([0, 25, 0, 25])
plt.grid(True)
plt.savefig('scatter_data.png')
plt.show()

我们创建了一个新的空白画布，并在画布上绘制了 X_train 和 y_train 的散点图。其中，‘r*’ 表示散点图用红色星形来表示，markersize=10 表示散点的大小为 10。

三、一元线性回归模型训练

from sklearn.linear_model import LinearRegression
model = LinearRegression();
model.fit(X_train,y_train);
y_train_pred = model.predict(X_train);
print('模型的表达式为: y = %0.3f * x + %0.3f' % (model.coef_[0][0], model.intercept_[0]));

我们通过导入 LinearRegression 类来引入线性回归模型，使用 LinearRegression() 创建一个名为 model 的线性回归模型对象，使用 fit() 方法将训练数据集 X_train 和 y_train 传入模型，以拟合数据集，使用 predict() 方法对训练数据集 X_train 进行预测，得到预测结果 y_train_pred，使用 coef_ 和 intercept_ 属性来获取模型的系数和截距。

y_train_pred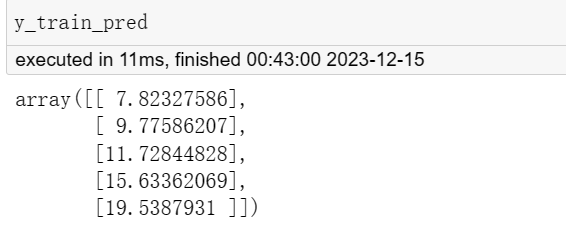

plt.figure()
plt.plot(X_train, y_train,'r*',markersize=10)
plt.plot(X_train, y_train_pred, 'b')  # 显示线性回归模型的直线
plt.title('披萨直径与价格的关系')
plt.xlabel('直径diameter (英寸)')
plt.ylabel('价格price (美元)')
plt.axis([0, 25, 0, 25])
plt.grid(True)
plt.savefig('regression_line.png')
plt.show()

使用 plt.figure()创建一个新的空白画布，使用 plt.plot() 方法绘制散点图，将训练数据集 X_train 和 y_train 以红色星形的形式绘制出来，将 X_train 和线性回归模型对训练数据集的预测结果 y_train_pred 以蓝色直线的形式绘制出来。

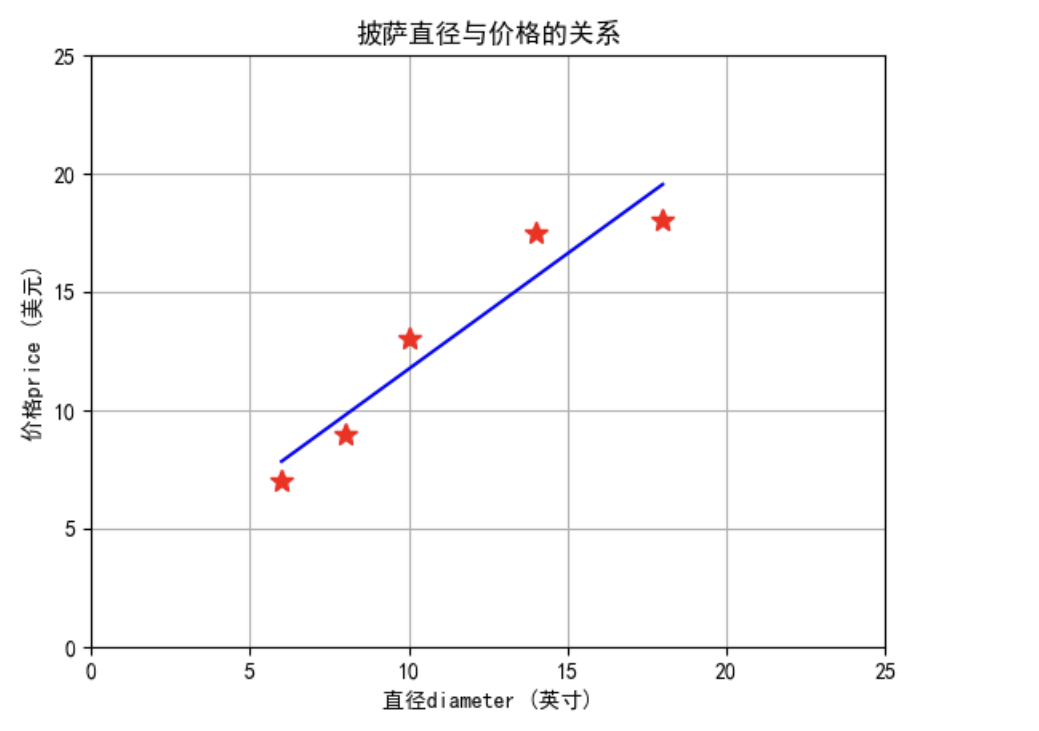
四、一元线性回归模型评估

while True:x_pre = input("请输入单个披萨的直径(输入q退出):")if x_pre == 'q':breakelse:x_prel = [[float(x_pre)]]y_pre = model.predict(x_prel)print('预测 {0} 英寸匹萨价格为: ${1:.2f}'.format(x_pre, y_pre[0][0]))
print('\n')

我们使用了一个循环，允许用户输入单个披萨的直径，并使用训练好的模型进行价格预测。

from sklearn.metrics import mean_squared_error
MSE_train = mean_squared_error(y_train, y_train_pred)  # 均方误差MSE
R2_score_train = model.score(X_train, y_train)  # 决定系数R2
print("一元回归模型的训练集的MSE: %0.3f，决定系数R^2: %0.3f" % (MSE_train, R2_score_train))

我们使用了sklearn.metrics模块中的mean_squared_error函数来计算训练集的均方误差（MSE），并使用模型的score方法计算训练集的决定系数（R2）。

X_test = [[8], [9],[11], [16], [12]]
y_test = [[11], [8.5], [15], [18], [14]]
y_test_pred = model.predict(X_test)
MSE_test = mean_squared_error(y_test, y_test_pred)
R2_score_test = model.score(X_test, y_test)
print("一元回归模型测试集的MSE: %0.3f，决定系数R^2: %0.3f" % (MSE_test, R2_score_test))
print('\n')

使用之前训练好的模型 model 对测试集的特征数据进行预测，得到预测结果 y_test_pred。

使用 mean_squared_error 函数计算测试集的均方误差（MSE），将实际的测试集标签 y_test 和模型对测试集的预测结果 y_test_pred 作为输入参数。

使用模型的 score 方法计算测试集的决定系数（R2），将测试集特征数据 X_test 和测试集标签 y_test 作为输入参数。

---

总结

我们首先收集了一组包括披萨尺寸和价格的数据样本。通过查看数据的特征和分布情况，我们发现披萨尺寸与价格之间呈现出一定的线性关系。然后，我们使用收集到的数据构建了一个线性回归模型。

模型的自变量是披萨的尺寸，因变量是披萨的价格。我们将数据集分为训练集和测试集，并使用训练集对模型进行了训练。在训练过程中，我们使用了均方误差（Mean Squared Error）作为评估指标来衡量模型的拟合程度。

经过训练后，我们对模型进行了评估。通过将测试集中的披萨尺寸输入模型，我们得到了相应的预测价格，并将其与真实价格进行对比，我们发现模型的预测结果与实际价格的差距比较小，表明模型对于预测披萨价格具有一定的准确性。