(CVPR-2022)感知优先的扩散模型训练

感知优先的扩散模型训练

Paper Title：Perception Prioritized Training of Diffusion Models

Paper是首尔国立大学数据科学与人工智能实验室发表在CVPR 2022的工作

论文地址

Code地址

Abstract

扩散模型通过优化相应损失项的加权和（即去噪得分匹配损失）来学习恢复被不同程度的噪声破坏的噪声数据。在本文中，我们表明，恢复被某些噪声水平破坏的数据为模型学习丰富的视觉概念提供了适当的代理任务。我们建议通过重新设计目标函数的加权方案，在训练期间优先考虑此类噪声水平。我们表明，无论数据集、架构和采样策略如何，我们对加权方案的简单重新设计都可以显著提高扩散模型的性能。

1. Introduction

扩散模型 [14, 36] 是近期出现的一类生成模型，已实现卓越的图像生成性能。扩散模型得到了迅速研究，因为它们为图像合成提供了几个理想的特性，包括稳定的训练、易于模型扩展和良好的分布覆盖率 [27]。从 Ho 等人 [14] 开始，最近的研究 [8, 27, 40] 表明，扩散模型可以渲染出与生成对抗网络 (GAN) [12] 生成的图像相当的高保真图像，尤其是在类条件设置下，这要依靠分类器指导 [8] 和级联模型 [32] 等额外努力。
然而，单一模型的无条件生成仍有很大的改进空间，而且尚未探索各种高分辨率数据集（例如 FFHQ [20]、MetFaces [18]）的性能，而其他生成模型系列 [3, 11, 20, 22, 41] 主要在这些数据集上竞争。

从易处理的噪声分布开始，扩散模型通过逐步消除噪声来生成图像。为了实现这一点，模型会学习预定义扩散过程的逆过程，即依次破坏具有不同噪声级别的图像内容。通过优化不同噪声水平 [39] 的去噪分数匹配损失 [43] 的总和来训练模型，旨在学习从损坏的图像中恢复干净的图像。Ho 等人 [14] 观察到，与使用简单的损失总和相比，他们通过经验获得的加权损失总和对样本质量更有利。他们的加权目标是目前训练扩散模型的事实标准目标 [8, 25, 27, 32, 40]。然而，令人惊讶的是，人们仍然不知道为什么这种方法表现良好，也不知道它是否对样本质量是最佳的。据我们所知，尚未探索设计一种更好的加权方案来实现更好的样本质量。

鉴于采用标准加权目标的扩散模型取得了成功，我们旨在通过探索更合适的目标函数加权方案来扩大这一优势。然而，由于两个因素，设计加权方案很困难。首先，噪声级别有数千个；因此，不可能进行详尽的网格搜索。其次，在训练过程中，模型在每个噪声级别上学习到什么信息并不清楚，因此很难确定每个级别的优先级。

在本文中，我们首先研究扩散模型在每个噪声级别上学习的内容。我们的主要直觉是，扩散模型通过解决每个级别的代理任务来学习丰富的视觉概念，即从损坏的图像中恢复图像。在图像略微损坏的噪声级别，图像已经可用于感知丰富的内容，因此，恢复图像不需要事先了解图像上下文。例如，该模型可以从相邻的干净像素中恢复噪声像素。因此，该模型学习难以察觉的细节，而不是高级上下文。相反，当图像严重损坏以致内容无法识别时，模型会学习感知可识别的内容来解决给定的代理任务。我们的观察促使我们提出 P2（感知优先）加权，旨在优先解决更重要的噪声级别的代理任务。我们为模型学习感知丰富内容的级别的损失分配更高的权重，而为模型学习难以察觉的细节分配最小权重。

为了验证所提出的 P2 加权的有效性，我们首先在各种数据集上比较了使用先前的标准加权方案和 P2 加权训练的扩散模型。使用我们的目标训练的模型始终大大优于先前的标准目标。
此外，我们表明，使用我们的目标训练的扩散模型在 CelebAHQ [17] 和 Oxford-flowers [28] 数据集上实现了最佳性能，在 FFHQ [20] 上实现了与各种类型的生成模型（包括生成对抗网络 (GAN) [12]）相当的性能。我们进一步分析了 P2 加权对各种模型配置和采样步骤是否有效。我们的主要贡献如下：

我们引入了一种简单有效的训练目标加权方案，以鼓励模型学习丰富的视觉概念。
我们研究了扩散模型如何从每个噪声级别学习视觉概念。
我们展示了扩散模型在各种数据集、模型配置和采样步骤中的持续改进。

2. Background

2.1. Definitions

扩散模型 [14, 36] 将复杂的数据分布 $p_{\text{data}}(x)$ 转换为简单的噪声分布 $\mathcal{N}(0, \mathbf{I})$ ，并学习从噪声中恢复数据。扩散模型的扩散过程通过预定义的噪声尺度 $\beta_1, \beta_2, \ldots, \beta_T < 1$ ，按时间步 $t$ 进行索引，逐渐破坏数据 $x_0$ 。受损数据 $x_1, \ldots, x_T$ 是从数据 $x_0 \sim p_{\text{data}}(x)$ 中采样的，扩散过程定义为高斯转移：

$q\left(x_t \mid x_{t-1}\right)=\mathcal{N}\left(x_t ; \sqrt{1-\beta_t} x_{t-1}, \beta_t \mathbf{I}\right)$

噪声数据 $x_t$ 可以直接从 $x_0$ 采样：

$x_t=\sqrt{\alpha_t} x_0 + \sqrt{1-\alpha_t} \epsilon$

其中 $\epsilon \sim \mathcal{N}(0, \mathbf{I})$ 且 $\alpha_t:=\prod_{s=1}^t\left(1-\beta_s\right)$ 。我们注意到，数据 $x_0$ 、噪声数据 $x_1, \ldots, x_T$ 和噪声 $\epsilon$ 具有相同的维度。为了确保 $p\left(x_T\right) \sim \mathcal{N}(0, \mathbf{I})$ 并确保扩散过程的可逆性 [36]，应将 $\beta_t$ 设为较小值，并使 $\alpha_T$ 接近零。为此，Ho 等人 [14] 和 Dhariwal 等人 [8] 使用线性噪声计划，其中 $\beta_t$ 从 $\beta_1$ 线性增加到 $\beta_T$ 。Nichol 等人 [27] 使用余弦计划，其中 $\alpha_t$ 类似于余弦函数。

扩散模型通过学习到的去噪过程 $p_\theta\left(x_{t-1} \mid x_t\right)$ 生成数据 $x_0$ ，该过程反转扩散过程（方程(1)）。从噪声 $x_T \sim \mathcal{N}(0, \mathbf{I})$ 开始，我们迭代地减去噪声预测器 $\epsilon_\theta$ 预测的噪声：

$x_{t-1}=\frac{1}{\sqrt{1-\beta_t}}\left(x_t-\frac{\beta_t}{\sqrt{1-\alpha_t}} \epsilon_\theta\left(x_t, t\right)\right) + \sigma_t z$

其中 $\sigma_t^2$ 是去噪过程中的方差，且 $\sim \mathcal{N}(0, \mathbf{I})$ 。Ho 等人 [14] 将 $\beta_t$ 用作 $\sigma_t^2$ 。

最近的工作 Kingma 等人 [23] 从信噪比 (SNR) 的角度简化了扩散模型中的噪声计划。根据方程 (2)，受损数据 $x_t$ 的 SNR 是均值和方差的平方比，可以表示为：

$\operatorname{SNR}(t) = \alpha_t / \left(1-\alpha_t\right)$

因此，噪声数据 $x_t$ 的方差可以用 SNR 表示为： $\alpha_t = 1 - 1 / (1 + \operatorname{SNR}(t))$ 。我们注意到 $\operatorname{SNR}(t)$ 是一个单调递减的函数。

2.2. Training Objectives

扩散模型是一种变分自编码器 (VAE)；其中编码器被定义为固定的扩散过程，而不是可学习的神经网络，解码器被定义为一个可学习的去噪过程，用来生成数据。类似于 VAE，我们可以通过优化变分下界 (VLB) 来训练扩散模型，它是去噪评分匹配损失的总和 [43]： $L_{vlb}=\sum_t L_t$ ，其中每个损失项的权重是均匀的。对于每个时间步 $t$ ，去噪评分匹配损失 $L_t$ 是两个高斯分布之间的距离，它可以根据噪声预测器 $\epsilon_\theta$ 重新表示为：

$\begin{aligned} L_t & =D_{KL}\left(q\left(x_{t-1} \mid x_t, x_0\right) \| p_\theta\left(x_{t-1} \mid x_t\right)\right) \\ & =\mathbb{E}_{x_0, \epsilon}\left[\frac{\beta_t}{\left(1-\beta_t\right)\left(1-\alpha_t\right)}\left\|\epsilon-\epsilon_\theta\left(x_t, t\right)\right\|^2\right] \end{aligned}$

直观地说，我们训练神经网络 $\epsilon_\theta$ 来预测给定时间步 $t$ 时，添加到噪声图像 $x_t$ 中的噪声 $\epsilon$ 。
Ho 等人 [14] 通过实验证明，以下简化目标对采样质量更有利：

$L_{\text {simple }}=\sum_t \mathbb{E}_{x_0, \epsilon}\left[\left\|\epsilon-\epsilon_\theta\left(x_t, t\right)\right\|^2\right]$

从 VLB 的角度来看，他们的目标是 $L_{\text {simple }}=\sum_t \lambda_t L_t$ ，其中加权方案为 $\lambda_t=\left(1-\beta_t\right)\left(1-\alpha_t\right) / \beta_t$ 。在连续时间设置中，该方案可以用信噪比 (SNR) 表示为：

$\lambda_t=-1 / \log -\operatorname{SNR}^{\prime}(t)=-\operatorname{SNR}(t) / \operatorname{SNR}^{\prime}(t)$

其中 $\operatorname{SNR}^{\prime}(t)=\frac{d \operatorname{SNR}(t)}{d t}$ 。推导过程见附录。
Ho 等人 [14] 使用固定的方差 $\sigma_t$ 值，而 Nichol 等人 [27] 提出通过混合目标 $L_{\text {hybrid }}=L_{\text {simple }}+c L_{vlb}$ 来学习方差 $\sigma_t$ ，其中 $c=1 e^{-3}$ 。他们观察到，学习 $\sigma_t$ 可以减少采样步骤，同时保持生成性能。我们继承了他们的混合目标以提高采样效率，并修改了 $L_{\text {simple }}$ 以提高性能。

2.3. Evaluation Metrics

我们使用 FID [13] 和 KID [2] 进行定量评估。众所周知，FID 类似于人类感知 [13]，并且被广泛用作衡量生成性能的默认指标 [8、11、18、20、30]。KID 是一种常用的指标，用于衡量小数据集上的性能 [18、19、30]。但是，由于这两个指标都对预处理 [30] 很敏感，因此我们使用正确实现的库 [30]。
我们计算生成的样本和整个训练集之间的 FID 和 KID。我们用 50k 个样本测量了最终得分，并用 10k 个样本进行了消融研究以了解效率，遵循 [8]。我们分别将它们表示为 FID50k 和 FID-10k。

3. Method

我们首先在第 3.1 节中研究模型在每个扩散步骤中学习的内容。然后，我们在第 3.2 节中提出我们的加权方案。我们在第 3.3 节中讨论了我们的加权方案如何有效。

3.1. Learning to Recover Signals from Noisy Data

扩散模型通过在每个噪声级别上解决预任务来学习视觉概念，这个预任务是从损坏的信号中恢复信号。更具体地说，模型预测噪声图像 $x_t$ 中的噪声分量 $\epsilon$ ，其中时间步 $t$ 是噪声级别的索引。虽然扩散模型的输出是噪声，其他生成模型（如VAE、GAN）则直接输出图像。由于噪声不包含任何内容或信号，因此很难理解噪声预测是如何有助于学习丰富的视觉概念的。扩散模型的这种特性引发了以下问题：模型在训练的每一步中学习到了什么信息？

研究扩散过程。我们首先研究预定义的扩散过程，以探索模型能从每个噪声级别学习到什么。假设我们有两个不同的干净图像 $x_0, x_0^{\prime}$ 和三个噪声图像 $x_{t A}, x_{t B} \sim q\left(x_t \mid x_0\right), x_t^{\prime} \sim q\left(x_t \mid x_0^{\prime}\right)$ ，其中 $q$ 是扩散过程。在图1（左）中，我们测量了两种情况下的感知距离（LPIPS [46]）： $x_{t A}$ 和 $x_{t B}$ 之间的距离（蓝线），它们共享相同的 $x_0$ ，以及 $x_{t A}$ 和 $x_t^{\prime}$ 之间的距离（橙线），它们是从不同的图像 $x_0$ 和 $x_0^{\prime}$ 合成的。我们展示了这两种情况下的距离作为信噪比（SNR）的函数，SNR 在公式 (4) 中引入，用于表征每一步的噪声级别。简要回顾一下，SNR 在扩散过程中减少，如图1（右）所示，在去噪过程中增加。

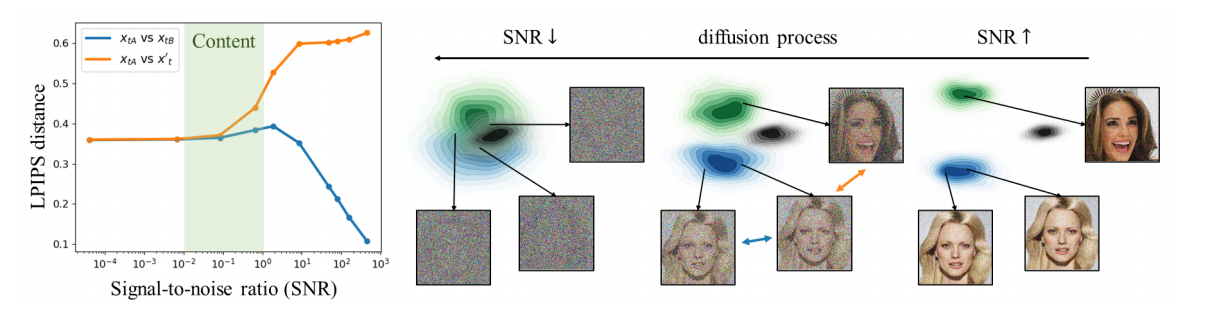
图1. 扩散过程中的信息移除。（左）受损图像的感知距离与信噪比（SNR）的关系。距离是从同一图像（蓝色）或不同图像（橙色）损坏的两幅噪声图像之间测量的。我们对CelebA-HQ数据集中的200个随机三元组进行距离测量并取平均。当SNR的幅度在 $10^{-2}$ 到 $10^{\circ}$ 之间时，可感知的内容被移除。（右）扩散过程的示意图。

扩散过程的早期步骤具有较大的SNR，这表明噪声几乎不可见；因此，噪声图像 $x_t$ 保留了大量来自干净图像 $x_0$ 的内容。因此，在早期步骤中， $x_{t A}$ 和 $x_{t B}$ 在感知上是相似的，而 $x_{t A}$ 和 $x_t^{\prime}$ 在感知上是不同的，如图1（左）中的高SNR侧所示。在SNR较大的情况下，模型可以在不理解整体上下文的情况下恢复信号，因为感知丰富的信号已经存在于图像中。因此，模型在解决恢复任务时，只能学习到难以察觉的细节。

相比之下，扩散过程的后期步骤具有较小的SNR，表明噪声足够大，足以移除 $x_0$ 的内容。因此，两种情况下的距离开始收敛到一个常数值，因为噪声图像变得难以识别高层次内容。这在图1（左）的低SNR侧显示出来。在这个阶段，模型需要先验知识来恢复信号，因为噪声图像缺乏可识别的内容。我们认为，模型在解决恢复任务时，当SNR较小时会学习到感知丰富的内容。

调查已训练的模型。我们希望验证前述讨论的内容。给定输入图像 $x_0$ ，我们首先通过扩散过程 $q\left(x_t \mid x_0\right)$ 将其扰动为 $x_t$ ，然后使用已学习的去噪过程 $p_\theta\left(\hat{x}_0 \mid x_t\right)$ 对其进行重构，如图2（左）所示。当 $t$ 较小时，由于扩散过程只移除少量信息，重构的 $\hat{x}_0$ 将与输入 $x_0$ 高度相似；当 $t$ 较大时， $\hat{x}_0$ 与 $x_0$ 共享的内容将减少。在图2（右）中，我们比较了不同 $t$ 值下的 $x_0$ 和 $\hat{x}_0$ ，以展示每一步如何为样本生成做出贡献。前两列的样本仅与最右列的输入共享粗略特征（如全局颜色方案），而第三、第四列的样本则共享可感知的区分内容。这表明，当第 $t$ 步的 SNR 小于 $10^{-2}$ 时，模型学习的是粗略特征；当 SNR 在 $10^{-2}$ 和 $10^{\circ}$ 之间时，模型学习的是内容。当 SNR 大于 $10^0$ （第五列）时，重构的图像在感知上与输入几乎相同，这表明模型学习了不会影响感知上可识别内容的细微细节。

图2. 随机重构。（左）重构的示意图，其中样本是从完整采样链中获得的。（右）右列为输入图像 $x_0$ ，底部为 $x_t$ 的 SNR。第1列和第2列的样本仅与输入共享粗略属性（例如，全局颜色结构）。第3列和第4列的样本与输入共享感知上区分性的内容。第5列与输入几乎相同，表明当 SNR 较大时，模型学习了不可感知的细节。

基于上述观察，我们假设扩散模型在小 SNR $\left(0-10^{-2}\right)$ 的步骤中学习粗略特征（例如，全局颜色结构），在中等 SNR $\left(10^{-2}-10^0\right)$ 中学习感知丰富的内容，以及在大 SNR $\left(10^0-10^4\right)$ 中去除剩余的噪声。根据我们的假设，我们将噪声水平分为三个阶段，分别称为粗略阶段、内容阶段和清理阶段。

3.2. Perception Prioritized Weighting

在上一节中，我们探讨了扩散模型在 SNR 方面从每个步骤中学到的东西。我们讨论了模型学习粗略特征（例如，全局颜色结构）、感知丰富的内容，并在三组噪声级别清理剩余噪声。我们指出，模型在清理阶段学习难以察觉的细节。在本节中，我们介绍了感知优先 (P2) 加权，这是一种新的训练目标加权方案，旨在优先从更重要的噪声级别学习。

我们选择将最小权重分配给不必要的清理阶段，从而将相对较高的权重分配给其余阶段。具体而言，我们旨在强调在内容阶段的训练，以鼓励模型学习感知丰富的上下文。为此，我们构建了以下加权方案：

$\lambda_t^{\prime}=\frac{\lambda_t}{(k+\operatorname{SNR}(t))^\gamma}$

其中， $\lambda_t$ 是之前的标准加权方案（公式（7））， $\gamma$ 是控制下调权重对学习不可感知细节关注强度的超参数。 $k$ 是防止极小 SNR 导致权重爆炸的超参数，并决定加权方案的尖锐度。尽管可以有多种设计，但我们展示了即使是最简单的选择（P2）也优于标准方案 $\lambda_t$ 。我们的方法可以通过将 $\sum_t \lambda_t L_t$ 替换为 $\sum_t \lambda_t^{\prime} L_t$ 应用于现有的扩散模型。

实际上，我们的加权方案 $\lambda_t^{\prime}$ 是 Ho 等人 [14]（公式（7））所用的 $\lambda_t$ 加权方案的推广，其中 $\lambda_t^{\prime}$ 在 $\gamma=0$ 时变为 $\lambda_t$ 。我们在此将 $\lambda_t$ 称为基线方案。

3.3. Effectiveness of P2 Weighting

先前的研究 $[14, 27]$ 通过实验证明，基线目标 $\sum_t \lambda_t L_t$ 为样本质量提供了比 VLB 目标 $\sum_t L_t$ 更好的归纳偏置，后者在训练过程中不施加任何归纳偏置。图 3 展示了线性 [14] 和余弦 [27] 噪声调度的 $\lambda_t^{\prime}$ 和 $\lambda_t$ ，这在第 2.1 节中进行了说明，表明两种加权方案都将训练重点放在内容阶段，最少关注清理阶段。基线加权的成功与我们之前的假设一致，即模型通过在内容阶段解决预设任务来学习感知丰富的内容。

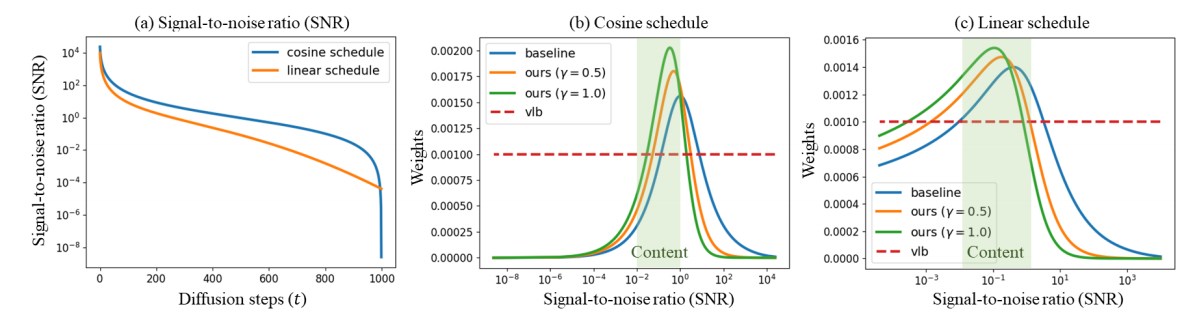
图 3. 加权方案。（左）线性和余弦噪声计划的信噪比 (SNR) 供参考。（中）我们的 P2 加权和采用余弦计划的基线的权重。（右）P2 加权和采用线性计划的基线的权重。
与基线相比，P2 加权会抑制大 SNR 的权重，此时模型会学习难以察觉的细节。

图 4. 通过在 FFHQ 上进行训练对 FID-10k 进行比较。
P2 加权持续提高线性和余弦计划的性能。训练进度是指模型看到的图像数量。样本以 250 步生成。

然而，尽管基线目标取得了成功，我们认为基线目标仍然对学习不可察觉的细节给予了不应有的关注，并阻碍了对感知丰富内容的学习。图 3 显示，我们的 $\lambda_t^{\prime}$ 进一步压制了清理阶段的权重，相对提升了粗略和内容阶段的权重。为了直观展示权重的相对变化，我们展示了归一化的加权方案。图 4 支持我们的方法，因为使用我们加权方案 $(\gamma=1)$ 训练的扩散模型在整个训练过程中，其 FID 对于线性和余弦调度都优于基线。

图 4 中另一个值得注意的结果是，尽管我们的加权方案大大提高了 FID，但余弦方案仍远不如线性方案。等式 (5) 表明加权方案与噪声方案密切相关。如图 3 所示，与线性方案相比，余弦方案为内容阶段分配的权重较小。我们要注意的是，设计加权方案和噪声方案是相关的，但不等同，因为噪声方案会影响权重和 MSE 项。
总而言之，我们的 P2 加权通过提升粗略和内容阶段的权重并抑制清理阶段的权重，为学习丰富的视觉概念提供了良好的归纳偏差。

3.4. Implementation

我们将 $k$ 设置为 1 以便于部署，因为 $/(1+\operatorname{SNR}(t))=1-\alpha_t$ ，如第 2.1 节所述。我们将 $\gamma$ 设置为 0.5 或 1。我们通过实验观察到，当 $\gamma$ 超过 2 时，样本中会出现噪声伪影，因为它几乎将清理阶段的权重设为零。我们将 $T = 1000$ 设置为所有实验的时间步数。我们在 ADM [8] 之上实现了所提出的方法，ADM 提供了设计精良的架构和高效的采样。我们在实验中使用了 ADM 的轻量版本。