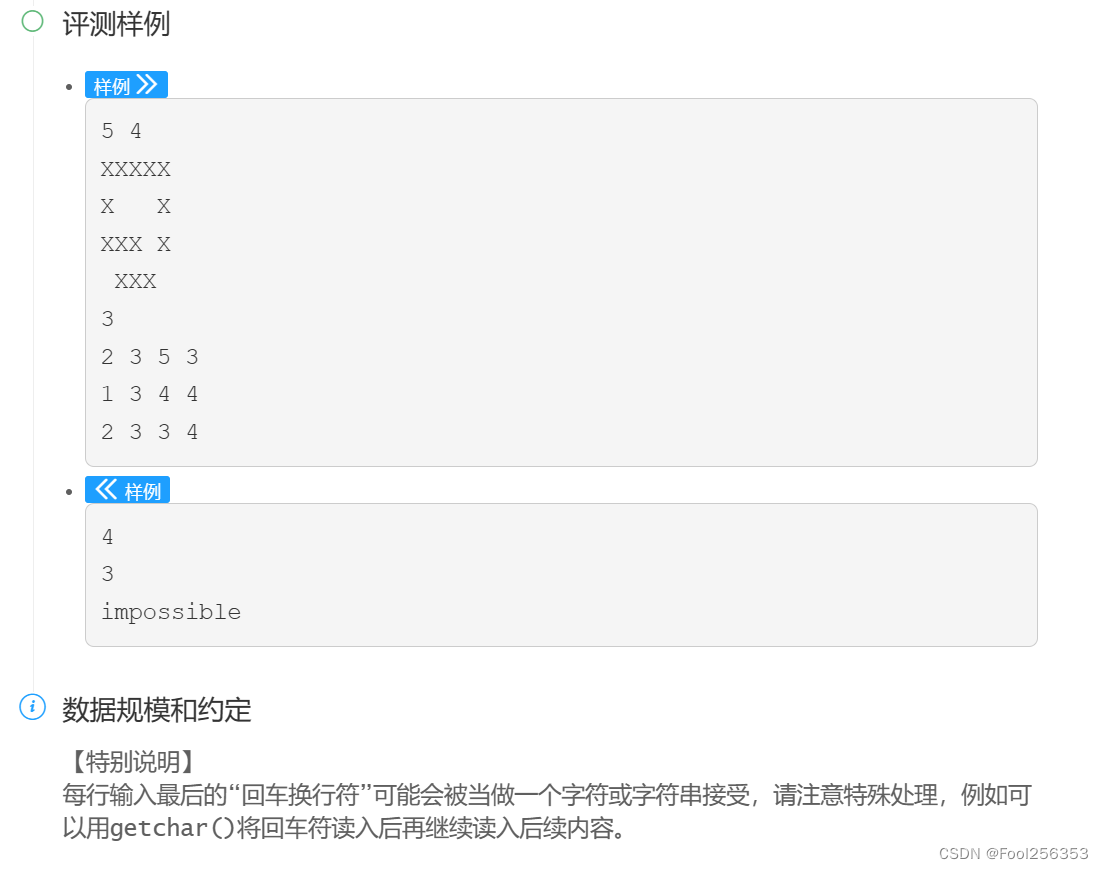
连通块+记忆性递归的综合运用
这里x,y的设置反我平常的习惯,搞得我有点晕
实际上可以一输入就交换x,y的数据的
如果设置y1为全局变量的话会warning:
warning: built-in function 'y1' declared as non-function
所以我改成p和q了
刚开始判断能不能相连是靠连通块
后面求最短线段数是靠记忆性递归
代码如下:
#include<stdio.h>
struct Min{int x_d;//x轴的方向int y_d;//y轴的方向int len;
}min[77][77];
void fill(int color, int x, int y);
bool judge(int m1, int n1, int m2, int n2);
void dg(int y, int x, int color, int y_d, int x_d);
int map[77][77];
int w, h, p1, q1, p2, q2;int main(void)
{//板子输入scanf("%d%d", &w, &h);getchar();for(int i = 1; i <= h; i++){char c;for(int j = 1; j <= w; j++)if((c = getchar()) == 'X')map[i][j] = 1;elsemap[i][j] = 0;getchar();}//开始填充连通块int color = 2;fill(color++, 0, 0);for(int i = 1; i <= h; i++)for(int j = 1; j <= w; j++)if(map[i][j] == 0)fill(color++, i, j);//开始判断并计算int n;scanf("%d", &n);for(int i = 0; i < n; i++){scanf("%d%d%d%d", &p1, &q1, &p2, &q2);if(judge(p1, q1, p2, q2)){printf("impossible\n");continue;}//重置min数组for(int i = 0; i <= h + 1; i++)for(int j = 0; j <= w + 1; j++)min[i][j].len = 100, min[i][j].x_d = 0, min[i][j].y_d = 0;min[q1][p1].len = 0;//求最短线段数(从x1,y1到x2,y2)if(map[q1 + 1][p1] != 1) dg(q1 + 1, p1, map[q1 + 1][p1], 1, 0);if(map[q1 - 1][p1] != 1) dg(q1 - 1, p1, map[q1 - 1][p1], -1, 0);if(map[q1][p1 + 1] != 1) dg(q1, p1 + 1, map[q1][p1 + 1], 0, 1);if(map[q1][p1 - 1] != 1) dg(q1, p1 - 1, map[q1][p1 - 1], 0, -1);//得到最短线段数int minn = 100;if(map[q2 + 1][p2] != 1){int tmp = min[q2 + 1][p2].len + ((min[q2 + 1][p2].x_d == 0 && min[q2 + 1][p2].y_d == -1) ? 0 : 1);minn = (minn < tmp) ? minn : tmp;}if(map[q2 - 1][p2] != 1){int tmp = min[q2 - 1][p2].len + ((min[q2 - 1][p2].x_d == 0 && min[q2 - 1][p2].y_d == 1) ? 0 : 1);minn = (minn < tmp) ? minn : tmp;}if(map[q2][p2 + 1] != 1){int tmp = min[q2][p2 + 1].len + ((min[q2][p2 + 1].x_d == -1 && min[q2][p2 + 1].y_d == 0) ? 0 : 1);minn = (minn < tmp) ? minn : tmp;}if(map[q2][p2 - 1] != 1){int tmp = min[q2][p2 - 1].len + ((min[q2][p2 - 1].x_d == 1 && min[q2][p2 - 1].y_d == 0) ? 0 : 1);minn = (minn < tmp) ? minn : tmp;}//输出if(minn > 10) printf("impossible\n");else printf("%d\n", minn);}return 0;
}
void fill(int color, int x, int y)
{if(map[x][y]) return;if(x < 0 || y < 0 || x > h + 1 || y > w + 1) return;map[x][y] = color;fill(color, x + 1, y), fill(color, x - 1, y);fill(color, x, y + 1), fill(color, x, y - 1);return;
}
bool judge(int m1, int n1, int m2, int n2)
{int tmp1[4] = {map[n1 + 1][m1], map[n1 - 1][m1], map[n1][m1 + 1], map[n1][m1 - 1]};int tmp2[4] = {map[n2 + 1][m2], map[n2 - 1][m2], map[n2][m2 + 1], map[n2][m2 - 1]};for(int i = 0; i < 4; i++){if(tmp1[i] == 1) continue;for(int j = 0; j < 4; j++){if(tmp2[j] == 1) continue;if(tmp1[i] == tmp2[j]) return false;}}return true;//只是代表是否执行if,而不是能不能连通
}
void dg(int y, int x, int color, int y_d, int x_d)
{if(x < 0 || y < 0 || x > w + 1 || y > h + 1) return;if(map[y][x] != color) return;int tmp = min[y - y_d][x - x_d].len + ((x_d == min[y - y_d][x - x_d].x_d && y_d == min[y - y_d][x - x_d].y_d) ? 0 : 1);if(tmp > min[y][x].len) return;//等于的话不用返回min[y][x].len = tmp, min[y][x].x_d = x_d, min[y][x].y_d = y_d;dg(y + 1, x, color, 1, 0);dg(y - 1, x, color, -1, 0);dg(y, x + 1, color, 0, 1);dg(y, x - 1, color, 0, -1);return;
}这里实际上可以改一下目的地的color(本来是1),使旁边的块可以直接走到目的地,而不是目的地旁边
只要在4个方向的递归开始的时候改成相应的颜色就可以了,记得改回来,以后还要用
这样就不会显得累赘,可以把求最短线段数部分和得到最短线段数部分合并,代码会更短一点
懒得改了