克隆图[中等]

一、题目

给你无向连通图中一个节点的引用，请你返回该图的深拷贝（克隆）。图中的每个节点都包含它的值val（int）和其邻居的列表list[Node]。

class Node {public int val;public List<Node> neighbors;
}

测试用例格式：

简单起见，每个节点的值都和它的索引相同。例如，第一个节点值为1（val = 1），第二个节点值为2（val = 2），以此类推。该图在测试用例中使用邻接列表表示。

邻接列表是用于表示有限图的无序列表的集合。每个列表都描述了图中节点的邻居集。给定节点将始终是图中的第一个节点（值为1）。你必须将给定节点的拷贝作为对克隆图的引用返回。

示例 1：

输入：adjList = [[2,4],[1,3],[2,4],[1,3]]
输出：[[2,4],[1,3],[2,4],[1,3]]
解释：
图中有4个节点。
节点1的值是1，它有两个邻居：节点2和4。
节点2的值是2，它有两个邻居：节点1和3。
节点3的值是3，它有两个邻居：节点2和4。
节点4的值是4，它有两个邻居：节点1和3。

示例 2：

输入：adjList = [[]]
输出：[[]]
解释：输入包含一个空列表。该图仅仅只有一个值为1的节点，它没有任何邻居。

示例 3：

输入：adjList = []
输出：[]
解释：这个图是空的，它不含任何节点。

示例 4：

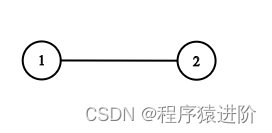
输入：adjList = [[2],[1]]
输出：[[2],[1]]

节点数不超过100。
每个节点值Node.val都是唯一的，1 <= Node.val <= 100。
无向图是一个简单图，这意味着图中没有重复的边，也没有自环。
由于图是无向的，如果节点p是节点q的邻居，那么节点q也必须是节点p的邻居。
图是连通图，你可以从给定节点访问到所有节点。

二、代码

【1】深度优先搜索： 对于本题而言，我们需要明确图的深拷贝是在做什么，对于一张图而言，它的深拷贝即构建一张与原图结构，值均一样的图，但是其中的节点不再是原来图节点的引用。因此，为了深拷贝出整张图，我们需要知道整张图的结构以及对应节点的值。由于题目只给了我们一个节点的引用，因此为了知道整张图的结构以及对应节点的值，我们需要从给定的节点出发，进行「图的遍历」，并在遍历的过程中完成图的深拷贝。

为了避免在深拷贝时陷入死循环，我们需要理解图的结构。对于一张无向图，任何给定的无向边都可以表示为两个有向边，即如果节点A和节点B之间存在无向边，则表示该图具有从节点A到节点B的有向边和从节点B到节点A的有向边。为了防止多次遍历同一个节点，陷入死循环，我们需要用一种数据结构记录已经被克隆过的节点。

算法：
1、使用一个哈希表存储所有已被访问和克隆的节点。哈希表中的key是原始图中的节点，value是克隆图中的对应节点。
2、从给定节点开始遍历图。如果某个节点已经被访问过，则返回其克隆图中的对应节点。
3、如果当前访问的节点不在哈希表中，则创建它的克隆节点并存储在哈希表中。注意：在进入递归之前，必须先创建克隆节点并保存在哈希表中。如果不保证这种顺序，可能会在递归中再次遇到同一个节点，再次遍历该节点时，陷入死循环。
4、递归调用每个节点的邻接点。每个节点递归调用的次数等于邻接点的数量，每一次调用返回其对应邻接点的克隆节点，最终返回这些克隆邻接点的列表，将其放入对应克隆节点的邻接表中。这样就可以克隆给定的节点和其邻接点。

class Solution {private HashMap <Node, Node> visited = new HashMap <> ();public Node cloneGraph(Node node) {if (node == null) {return node;}// 如果该节点已经被访问过了，则直接从哈希表中取出对应的克隆节点返回if (visited.containsKey(node)) {return visited.get(node);}// 克隆节点，注意到为了深拷贝我们不会克隆它的邻居的列表Node cloneNode = new Node(node.val, new ArrayList());// 哈希表存储visited.put(node, cloneNode);// 遍历该节点的邻居并更新克隆节点的邻居列表for (Node neighbor: node.neighbors) {cloneNode.neighbors.add(cloneGraph(neighbor));}return cloneNode;}
}

时间复杂度： O(N)，其中N表示节点数量。深度优先搜索遍历图的过程中每个节点只会被访问一次。
空间复杂度： O(N)。存储克隆节点和原节点的哈希表需要O(N)的空间，递归调用栈需要O(H)的空间，其中H是图的深度，经过放缩可以得到O(H)=O(N)，因此总体空间复杂度为O(N)。

【2】广度优先遍历： 同样，我们也可以用广度优先搜索来进行「图的遍历」。方法一与方法二的区别仅在于搜索的方式。深度优先搜索以深度优先，广度优先搜索以广度优先。这两种方法都需要借助哈希表记录被克隆过的节点来避免陷入死循环。

算法：
1、使用一个哈希表visited存储所有已被访问和克隆的节点。哈希表中的key是原始图中的节点，value是克隆图中的对应节点。
2、将题目给定的节点添加到队列。克隆该节点并存储到哈希表中。
3、每次从队列首部取出一个节点，遍历该节点的所有邻接点。如果某个邻接点已被访问，则该邻接点一定在visited中，那么从visited获得该邻接点，否则创建一个新的节点存储在visited中，并将邻接点添加到队列。将克隆的邻接点添加到克隆图对应节点的邻接表中。重复上述操作直到队列为空，则整个图遍历结束。

class Solution {public Node cloneGraph(Node node) {if (node == null) {return node;}HashMap<Node, Node> visited = new HashMap();// 将题目给定的节点添加到队列LinkedList<Node> queue = new LinkedList<Node> ();queue.add(node);// 克隆第一个节点并存储到哈希表中visited.put(node, new Node(node.val, new ArrayList()));// 广度优先搜索while (!queue.isEmpty()) {// 取出队列的头节点Node n = queue.remove();// 遍历该节点的邻居for (Node neighbor: n.neighbors) {if (!visited.containsKey(neighbor)) {// 如果没有被访问过，就克隆并存储在哈希表中visited.put(neighbor, new Node(neighbor.val, new ArrayList()));// 将邻居节点加入队列中queue.add(neighbor);}// 更新当前节点的邻居列表visited.get(n).neighbors.add(visited.get(neighbor));}}return visited.get(node);}
}