逆向获取某音乐软件的加密(js逆向)

本文仅用于技术交流，不得以危害或者是侵犯他人利益为目的使用文中介绍的代码模块，若有侵权请联系作者更改。

老套路，打开开发者工具，直接开始找到需要的数据位置，然后观察参数，请求头，cookie是否加密，我相信这部分内容大家都比较清楚。

第一个基本上，你均不影响结果，重要的还是他下方的内容

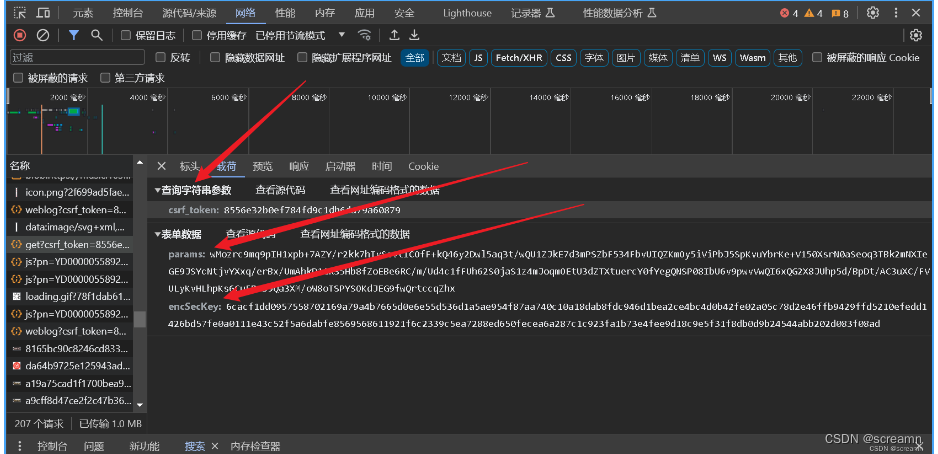
现在我们直接来照这个params参数，直接搜索，也可以打XHR断点快速找到这个位置，但是这里的话我推荐大家直接搜索，因为这个加密的参数不是字母代替的，而是一个英文单词，这样搜出来的内容可能会比xhr断点得到的更为准确，要是说加密参数是m="密文这种"，如果搜m=或者=m均出现大量情况的话，分析请求再来决定使用什么方法快速定位。

这边直接搜索,搜出来的也不少，但是他们均在一个文件中，那么我们可以缩小查找范围了，先开始点击查看。

进入文件后，直接搜索encSecKey，观察这里面是不是存在这个参数，直接找到，加密的两个参数的位置，所以说很多时候这种查找都是有技巧的，实在不行才去一个一个的查看。

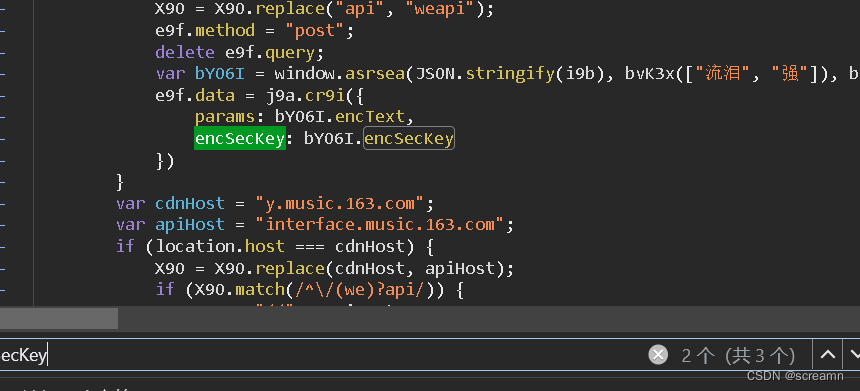
剩下的就是扣代码了，这个我只带大家扣一部分的代码，完整的还得大家去扣，主要是里面有些一些小坑，带大家过一下就行，剩下的纯缺啥补啥。

打上断点，开始调试

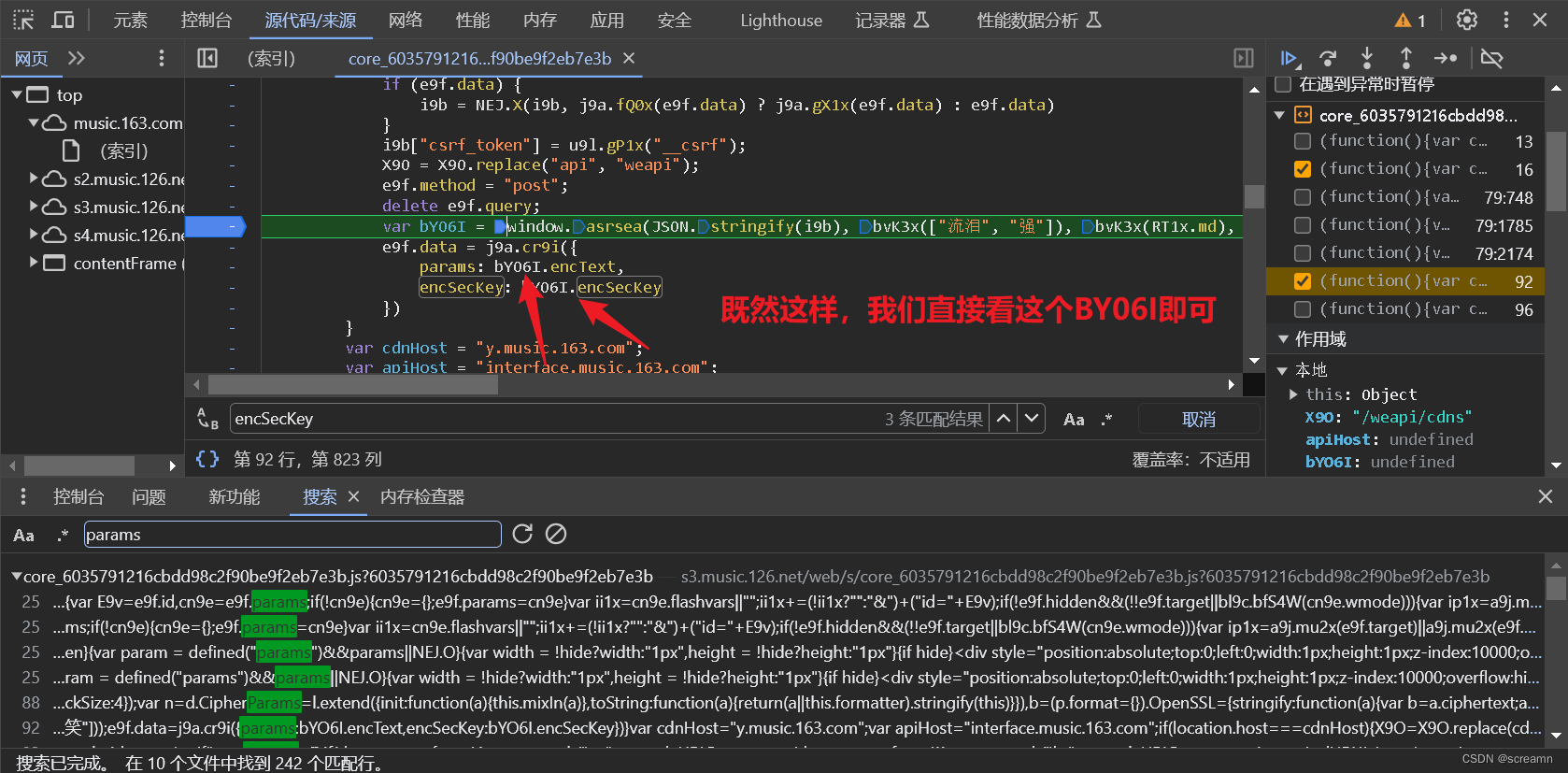
依次解析这里面的参数，避免存在加密的。固定值，多刷新几次发现没有改变。

依次进行后面的参数验证，我们发现全部都是常量，所以直接记录下来，直接拿来用。

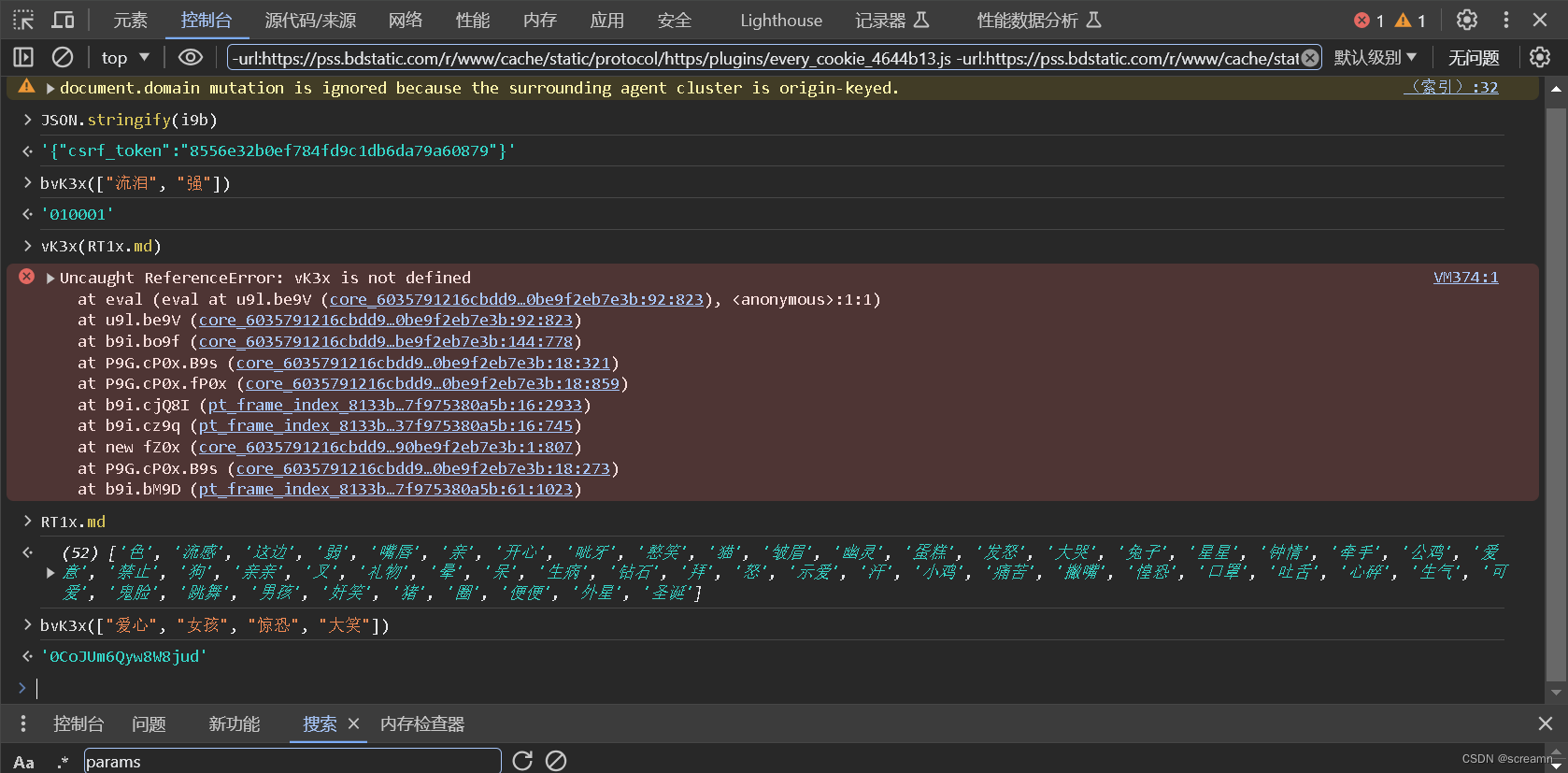
现在开始找加密形式。

开始补全这个内容，发现少a继续扣。

有其他的参数，扣下来a,继续扣。

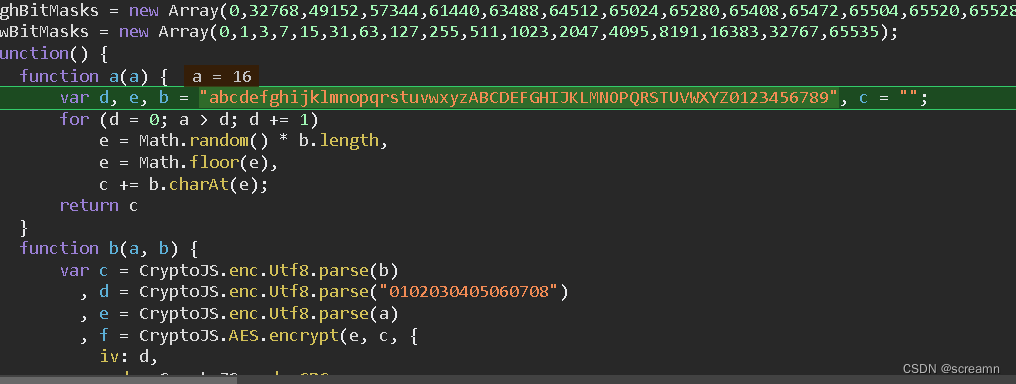
这个b函数我们需要注意一下，这里面的加密是通过js中的库函数加密的，所以我们在js中直接引用即可，剩下的都是扣代码，这边给出后续扣下来的代码。

function arrayCopy(a, b, c, d, e) {var g, h, f = Math.min(b + e, a.length);for (g = b,h = d; f > g; ++g,++h)c[h] = a[g]
}
function biFromNumber(a) {var c, b = new BigInt;for (b.isNeg = 0 > a,a = Math.abs(a),c = 0; a > 0;)b.digits[c++] = a & maxDigitVal,a >>= biRadixBits;return b
}
function reverseStr(a) {var c, b = "";for (c = a.length - 1; c > -1; --c)b += a.charAt(c);return b
}
function digitToHex(a) {var b = 15, c = "";for (i = 0; 4 > i; ++i)c += hexToChar[a & b],a >>>= 4;return reverseStr(c)
}
function biToHex(a) {var d, b = "";for (biHighIndex(a),d = biHighIndex(a); d > -1; --d)b += digitToHex(a.digits[d]);return b
}
function biModuloByRadixPower(a, b) {var c = new BigInt;return arrayCopy(a.digits, 0, c.digits, 0, b),c
}
function biDivideByRadixPower(a, b) {var c = new BigInt;return arrayCopy(a.digits, b, c.digits, 0, c.digits.length - b),c
}
function biMultiply(a, b) {var d, h, i, k, c = new BigInt, e = biHighIndex(a), f = biHighIndex(b);for (k = 0; f >= k; ++k) {for (d = 0,i = k,j = 0; e >= j; ++j,++i)h = c.digits[i] + a.digits[j] * b.digits[k] + d,c.digits[i] = h & maxDigitVal,d = h >>> biRadixBits;c.digits[k + e + 1] = d}return c.isNeg = a.isNeg != b.isNeg,c
}
function BarrettMu_multiplyMod(a, b) {var c = biMultiply(a, b);return this.modulo(c)
}
function BarrettMu_powMod(a, b) {var d, e, c = new BigInt;for (c.digits[0] = 1,d = a,e = b; ;) {if (0 != (1 & e.digits[0]) && (c = this.multiplyMod(c, d)),e = biShiftRight(e, 1),0 == e.digits[0] && 0 == biHighIndex(e))break;d = this.multiplyMod(d, d)}return c
}
function BarrettMu_modulo(a) {var i, b = biDivideByRadixPower(a, this.k - 1), c = biMultiply(b, this.mu), d = biDivideByRadixPower(c, this.k + 1), e = biModuloByRadixPower(a, this.k + 1), f = biMultiply(d, this.modulus), g = biModuloByRadixPower(f, this.k + 1), h = biSubtract(e, g);for (h.isNeg && (h = biAdd(h, this.bkplus1)),i = biCompare(h, this.modulus) >= 0; i;)h = biSubtract(h, this.modulus),i = biCompare(h, this.modulus) >= 0;return h
}
function biMultiplyByRadixPower(a, b) {var c = new BigInt;return arrayCopy(a.digits, 0, c.digits, b, c.digits.length - b),c
}
function biShiftRight(a, b) {var e, f, g, h, c = Math.floor(b / bitsPerDigit), d = new BigInt;for (arrayCopy(a.digits, c, d.digits, 0, a.digits.length - c),e = b % bitsPerDigit,f = bitsPerDigit - e,g = 0,h = g + 1; g < d.digits.length - 1; ++g,++h)d.digits[g] = d.digits[g] >>> e | (d.digits[h] & lowBitMasks[e]) << f;return d.digits[d.digits.length - 1] >>>= e,d.isNeg = a.isNeg,d
}
function biMultiplyDigit(a, b) {var c, d, e, f;for (result = new BigInt,c = biHighIndex(a),d = 0,f = 0; c >= f; ++f)e = result.digits[f] + a.digits[f] * b + d,result.digits[f] = e & maxDigitVal,d = e >>> biRadixBits;return result.digits[1 + c] = d,result
}
function biSubtract(a, b) {var c, d, e, f;if (a.isNeg != b.isNeg)b.isNeg = !b.isNeg,c = biAdd(a, b),b.isNeg = !b.isNeg;else {for (c = new BigInt,e = 0,f = 0; f < a.digits.length; ++f)d = a.digits[f] - b.digits[f] + e,c.digits[f] = 65535 & d,c.digits[f] < 0 && (c.digits[f] += biRadix),e = 0 - Number(0 > d);if (-1 == e) {for (e = 0,f = 0; f < a.digits.length; ++f)d = 0 - c.digits[f] + e,c.digits[f] = 65535 & d,c.digits[f] < 0 && (c.digits[f] += biRadix),e = 0 - Number(0 > d);c.isNeg = !a.isNeg} elsec.isNeg = a.isNeg}return c
}
function biCompare(a, b) {if (a.isNeg != b.isNeg)return 1 - 2 * Number(a.isNeg);for (var c = a.digits.length - 1; c >= 0; --c)if (a.digits[c] != b.digits[c])return a.isNeg ? 1 - 2 * Number(a.digits[c] > b.digits[c]) : 1 - 2 * Number(a.digits[c] < b.digits[c]);return 0
}
function biShiftLeft(a, b) {var e, f, g, h, c = Math.floor(b / bitsPerDigit), d = new BigInt;for (arrayCopy(a.digits, 0, d.digits, c, d.digits.length - c),e = b % bitsPerDigit,f = bitsPerDigit - e,g = d.digits.length - 1,h = g - 1; g > 0; --g,--h)d.digits[g] = d.digits[g] << e & maxDigitVal | (d.digits[h] & highBitMasks[e]) >>> f;return d.digits[0] = d.digits[g] << e & maxDigitVal,d.isNeg = a.isNeg,d
}
var maxDigits, ZERO_ARRAY, bigZero, bigOne, dpl10, lr10, hexatrigesimalToChar, hexToChar, highBitMasks, lowBitMasks, biRadixBase = 2, biRadixBits = 16, bitsPerDigit = biRadixBits, biRadix = 65536, biHalfRadix = biRadix >>> 1, biRadixSquared = biRadix * biRadix, maxDigitVal = biRadix - 1, maxInteger = 9999999999999998;
setMaxDigits(20),dpl10 = 15,lr10 = biFromNumber(1e15),hexatrigesimalToChar = new Array("0", "1", "2", "3", "4", "5", "6", "7", "8", "9", "a", "b", "c", "d", "e", "f", "g", "h", "i", "j", "k", "l", "m", "n", "o", "p", "q", "r", "s", "t", "u", "v", "w", "x", "y", "z"),hexToChar = new Array("0", "1", "2", "3", "4", "5", "6", "7", "8", "9", "a", "b", "c", "d", "e", "f"),highBitMasks = new Array(0, 32768, 49152, 57344, 61440, 63488, 64512, 65024, 65280, 65408, 65472, 65504, 65520, 65528, 65532, 65534, 65535),lowBitMasks = new Array(0, 1, 3, 7, 15, 31, 63, 127, 255, 511, 1023, 2047, 4095, 8191, 16383, 32767, 65535);function biNumBits(a) {var e, b = biHighIndex(a), c = a.digits[b], d = (b + 1) * bitsPerDigit;for (e = d; e > d - bitsPerDigit && 0 == (32768 & c); --e)c <<= 1;return e
}
function biDivideModulo(a, b) {var f, g, h, i, j, k, l, m, n, o, p, q, r, s, c = biNumBits(a), d = biNumBits(b), e = b.isNeg;if (d > c)return a.isNeg ? (f = biCopy(bigOne),f.isNeg = !b.isNeg,a.isNeg = !1,b.isNeg = !1,g = biSubtract(b, a),a.isNeg = !0,b.isNeg = e) : (f = new BigInt,g = biCopy(a)),new Array(f, g);for (f = new BigInt,g = a,h = Math.ceil(d / bitsPerDigit) - 1,i = 0; b.digits[h] < biHalfRadix;)b = biShiftLeft(b, 1),++i,++d,h = Math.ceil(d / bitsPerDigit) - 1;for (g = biShiftLeft(g, i),c += i,j = Math.ceil(c / bitsPerDigit) - 1,k = biMultiplyByRadixPower(b, j - h); -1 != biCompare(g, k);)++f.digits[j - h],g = biSubtract(g, k);for (l = j; l > h; --l) {for (m = l >= g.digits.length ? 0 : g.digits[l],n = l - 1 >= g.digits.length ? 0 : g.digits[l - 1],o = l - 2 >= g.digits.length ? 0 : g.digits[l - 2],p = h >= b.digits.length ? 0 : b.digits[h],q = h - 1 >= b.digits.length ? 0 : b.digits[h - 1],f.digits[l - h - 1] = m == p ? maxDigitVal : Math.floor((m * biRadix + n) / p),r = f.digits[l - h - 1] * (p * biRadix + q),s = m * biRadixSquared + (n * biRadix + o); r > s;)--f.digits[l - h - 1],r = f.digits[l - h - 1] * (p * biRadix | q),s = m * biRadix * biRadix + (n * biRadix + o);k = biMultiplyByRadixPower(b, l - h - 1),g = biSubtract(g, biMultiplyDigit(k, f.digits[l - h - 1])),g.isNeg && (g = biAdd(g, k),--f.digits[l - h - 1])}return g = biShiftRight(g, i),f.isNeg = a.isNeg != e,a.isNeg && (f = e ? biAdd(f, bigOne) : biSubtract(f, bigOne),b = biShiftRight(b, i),g = biSubtract(b, g)),0 == g.digits[0] && 0 == biHighIndex(g) && (g.isNeg = !1),new Array(f, g)
}
function biDivide(a, b) {return biDivideModulo(a, b)[0]
}
function biCopy(a) {var b = new BigInt(!0);return b.digits = a.digits.slice(0),b.isNeg = a.isNeg,b
}
function BarrettMu(a) {this.modulus = biCopy(a),this.k = biHighIndex(this.modulus) + 1;var b = new BigInt;b.digits[2 * this.k] = 1,this.mu = biDivide(b, this.modulus),this.bkplus1 = new BigInt,this.bkplus1.digits[this.k + 1] = 1,this.modulo = BarrettMu_modulo,this.multiplyMod = BarrettMu_multiplyMod,this.powMod = BarrettMu_powMod
}
function charToHex(a) {var h, b = 48, c = b + 9, d = 97, e = d + 25, f = 65, g = 90;return h = a >= b && c >= a ? a - b : a >= f && g >= a ? 10 + a - f : a >= d && e >= a ? 10 + a - d : 0
}
function hexToDigit(a) {var d, b = 0, c = Math.min(a.length, 4);for (d = 0; c > d; ++d)b <<= 4,b |= charToHex(a.charCodeAt(d));return b
}
function biFromHex(a) {var d, e, b = new BigInt, c = a.length;for (d = c,e = 0; d > 0; d -= 4,++e)b.digits[e] = hexToDigit(a.substr(Math.max(d - 4, 0), Math.min(d, 4)));return b
}
function BigInt(a) {this.digits = "boolean" == typeof a && 1 == a ? null : ZERO_ARRAY.slice(0),this.isNeg = !1
}
function biHighIndex(a) {for (var b = a.digits.length - 1; b > 0 && 0 == a.digits[b];)--b;return b
}
var CryptoJS = require('crypto-js')
function b(a, b) {var f = ""var c = CryptoJS.enc.Utf8.parse(b), d = CryptoJS.enc.Utf8.parse("0102030405060708"), e = CryptoJS.enc.Utf8.parse(a), f = CryptoJS.AES.encrypt(e, c, {iv: d,mode: CryptoJS.mode.CBC});return f.toString()
}
function a(a) {var d, e, b = "abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789", c = "";for (d = 0; a > d; d += 1)e = Math.random() * b.length,e = Math.floor(e),c += b.charAt(e);return c
}
function setMaxDigits(a) {maxDigits = a,ZERO_ARRAY = new Array(maxDigits);for (var b = 0; b < ZERO_ARRAY.length; b++)ZERO_ARRAY[b] = 0;bigZero = new BigInt,bigOne = new BigInt,bigOne.digits[0] = 1
}
function encryptedString(a, b) {for (var f, g, h, i, j, k, l, c = new Array, d = b.length, e = 0; d > e;)c[e] = b.charCodeAt(e),e++;for (; 0 != c.length % a.chunkSize;)c[e++] = 0;for (f = c.length,g = "",e = 0; f > e; e += a.chunkSize) {for (j = new BigInt,h = 0,i = e; i < e + a.chunkSize; ++h)j.digits[h] = c[i++],j.digits[h] += c[i++] << 8;k = a.barrett.powMod(j, a.e),l = 16 == a.radix ? biToHex(k) : biToString(k, a.radix),g += l + " "}return g.substring(0, g.length - 1)
}
function RSAKeyPair(a, b, c) {this.e = biFromHex(a),this.d = biFromHex(b),this.m = biFromHex(c),this.chunkSize = 2 * biHighIndex(this.m),this.radix = 16,this.barrett = new BarrettMu(this.m)
}
function c(a, b, c) {var d, e;return setMaxDigits(131),d = new RSAKeyPair(b, "", c),e = encryptedString(d, a)
}function cr8j(gF9w) {return (gF9w, "&", !0)
}

基本的思路学习，然后自己着手写一次，理解会更多，点个赞再走吧！