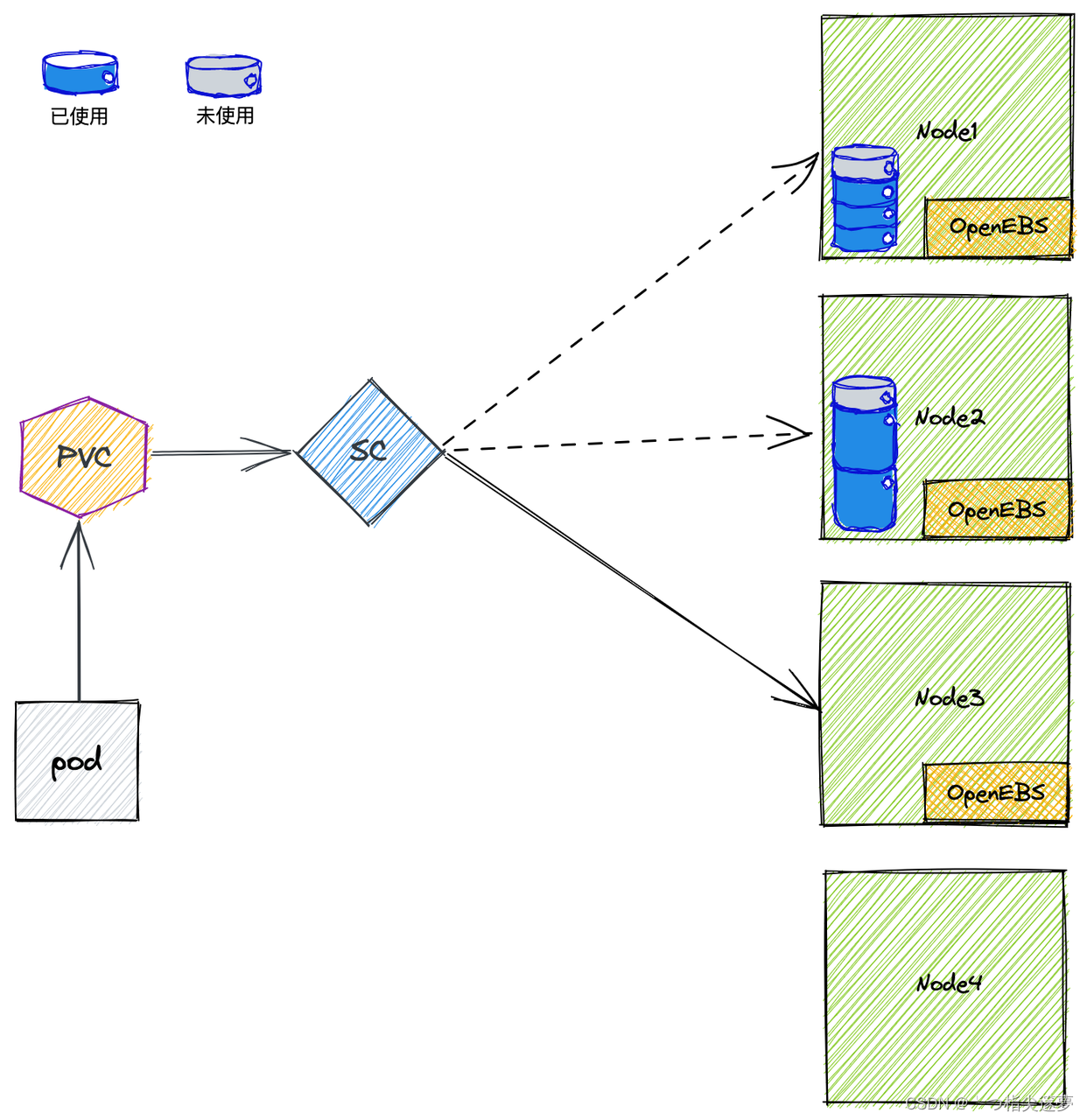
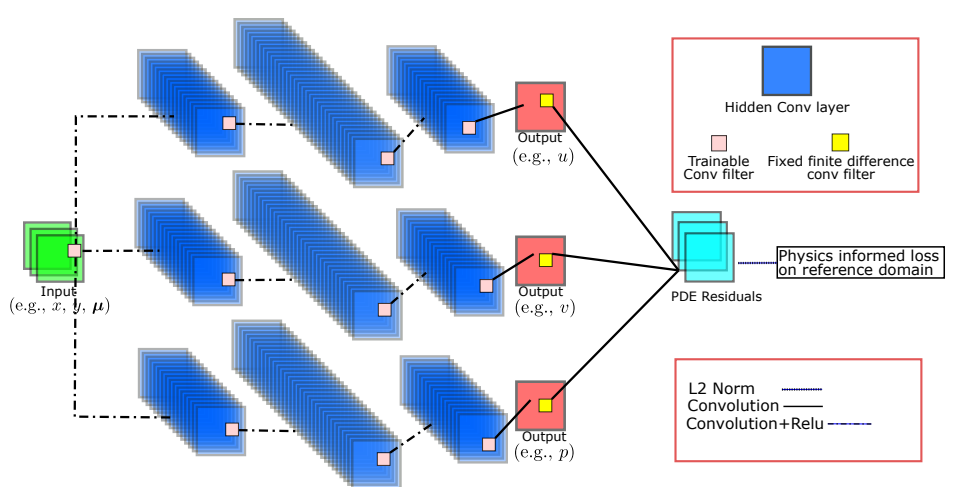
//声明版本号(程序中的版本号要和编译器版本号一致)
pragma solidity ^0.5.17;
//合约
contract EventTest
{//状态变量uint public Variable;//构造函数constructor() public{Variable = 100;}event ValueChanged(uint newValue); //事件声明event Log(string, uint);//调用该函数,修改状态变量的值并触发事件function setValue(uint newValue) public {Variable = newValue;emit ValueChanged(newValue); //触发事件emit Log("New_Variable = ", newValue); //记录日志}}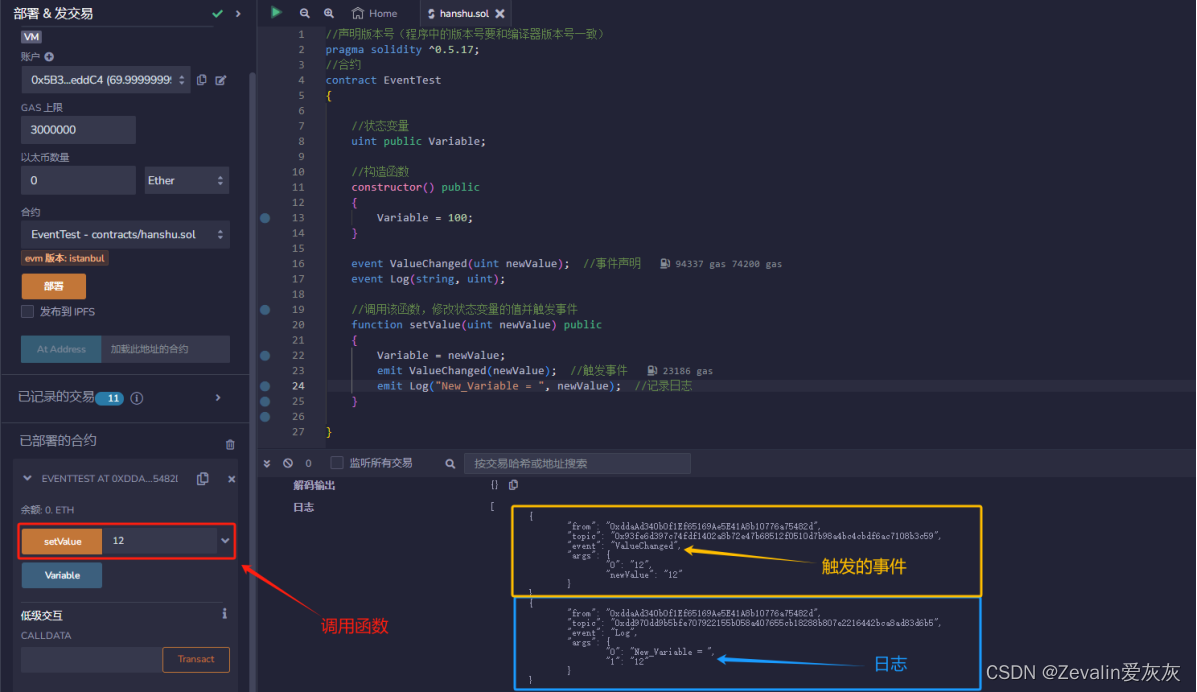
(1)事件用于记录在区块链上的特定活动,“emit ValueChanged(newValue);”语句的作用是触发ValueChanged事件(首先需要声明事件)。
①触发事件后会生成相应日志,上图黄框就是“emit ValueChanged(newValue);”语句产生的日志,其中“form”指的是触发事件的合约账户。
②事件主要是供外部应用程序监听,外部应用程序可以监听事件以获取合约中特定活动的通知。
(2)日志的作用是在智能合约中记录重要信息,“emit Log("New_Variable = ", newValue);”语句的作用就是生成一个日志(同样需要先声明,日志可以由字符串、整型等数据类型组成),通过以太坊区块链浏览器或特定工具可以查看记录的日志信息。
(3)触发事件和记录日志实际上是同一件事,声明时使用关键字event,触发时使用关键字emit,只是二者的目的不同,事件名一般按照实际行为命名,而日志常声明为“Log”或“log”。