偏微分方程（PDE）是数学中一门重要的分支，应用范围广泛涉及自然科学、工程技术、生物学领域等。然而我们都知道，偏微分方程的求解过程异常艰难，如果碰上了特别复杂的，传统的计算方法可能需要数百万个CPU小时。

怎么解决？神经网络这就来了！

经研究发现，深度学习神经网络求解可以大幅度提高效率，比传统的偏微分方程求解器更快地求出近似解。为此，更多人投入到了这个方向的研究中，基于神经网络的偏微分方程求解方法也成了研究新热点。

目前该方向主要分为 3 大类：数据驱动、物理约束、物理驱动。我根据这些类别帮大家整理了主流的26种神经网络偏微分方程求解方法，包含基于卷积神经网络的方法、基于全连接神经网络的方法、基于内嵌物理神经网络（PINN）及其改进的方法等等。

论文原文及代码看文末

1、数据驱动

基于 CNN

1.PDE-Net 2.0：Learning PDEs from data with a numeric-symbolic hybrid deep network

使用数值符号混合深度网络从数据中学习偏微分方程

「简述：」PDE-Net 2.0是一种基于深度学习的偏微分方程（PDE）发现方法。它通过结合数值近似和符号神经网络，从观察到的动态数据中发现（时变的）PDE。这种方法具有很高的灵活性和表达能力，可以学习到微分算子和底层PDE模型的非线性响应函数。实验结果表明，PDE-Net 2.0有潜力揭示观察到的动力学背后的隐藏PDE，并在噪声环境中预测较长时间的动力行为。

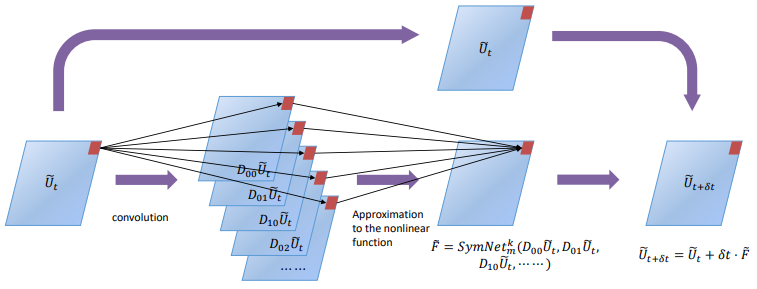
2.Convolution-Based Model-Solving Method for Three-Dimensional, Unsteady, Partial Differential Equations

基于卷积的三维非稳态偏微分方程模型求解方法

「简述：」论文提出3D-PDE-Net解决三维PDE问题。作者给出了一个数学推导，得出一个三维卷积核可以在表达能力的范围内近似任何阶数的微分算子，并在此基础上实现了3D-PDE-Net。通过最小化训练数据的标准化均方误差（NMSE），获得了最优网络，并采用L-BFGS作为优化的第二阶精度算法。数值实验结果表明，3D-PDE-Net使用少量训练样本即可获得良好的解精度，对于解决线性和非线性非定常PDE问题具有重要意义。

基于其他网络

1.Neural network as a function approximator and its application in solving differential equations

神经网络作为一种函数逼近器及其在解决微分方程中的应用

「简述：」本文探讨了神经网络在函数逼近方面的应用，并提出了一个通用的ODE和PDE求解器。求解器用于初始值问题和边界值问题的ODE，结果显示，对于未知函数及其导数，该求解器都具有高精度。相同的策略可以用于构建基于collocation points而不是mesh的PDE求解器，该求解器用于测试Burgers方程和热方程（即Laplace方程）。

2.Solving high-dimensional partial differential equations using deep learning

使用深度学习解决高维偏微分方程

「简述：」本文介绍了一种基于深度学习的方法，可以处理一般的高维抛物型偏微分方程（PDEs）。为此，使用向后随机微分方程重新表述PDEs，并使用神经网络近似未知解的梯度，非常类似于深度强化学习中梯度作为策略函数的思想。数值结果包括非线性Black-Scholes方程、Hamilton-Jacobi-Bellman方程和Allen-Cahn方程等示例表明，所提出的算法在高维情况下非常有效，无论在准确性还是成本方面都是如此。

3.Deep learning-based numerical methods for high-dimensional parabolic partial differential equations and backward stochastic differential equations

基于深度学习的高维抛物型偏微分方程和向后随机微分方程的数值方法

「简述：」本研究提出了一种解决高维抛物型偏微分方程（PDEs）和向后随机微分方程（BSDEs）的新算法。该算法通过将BSDE与强化学习进行类比，并将解的梯度视为策略函数，以及由规定的终端条件和BSDE的解之间的误差给出的损失函数，来构建算法。然后，像深度强化学习中一样，使用神经网络近似策略函数。使用TensorFlow进行的数值结果表明，所提出的算法对于物理学和金融学中的几个100维非线性PDEs非常有效和准确。

2、物理约束

PINN

1.Physics informed deeplearning (part I): Data-driven solutions of nonlinear partial differential equations

物理学启发的深度学习（第一部分）

「简述：」论文介绍了一种物理学启发的神经网络，可以同时解决监督学习任务和遵守物理定律。作者设计了两种算法类别，即连续时间模型和离散时间模型，来推导出数据驱动的解决方案和数据驱动的偏微分方程发现。这种神经网络是一种新型的数据高效的函数逼近器，能够自然地编码任何潜在的物理定律作为先验信息。在第一部分中，作者展示了如何使用这些网络推断偏微分方程的解，并获得完全可微分的、对所有输入坐标和自由参数具有物理意义的代理模型。

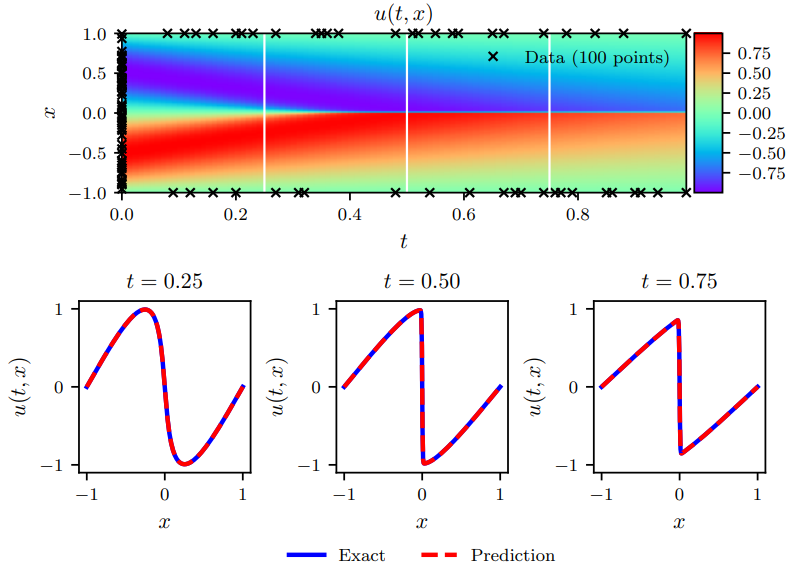
2.Physics Informed Deep Learning (Part II): Data-driven solutions of nonlinear partial differential equations

物理学启发的深度学习（第二部分）

「简述：」论文介绍了一种物理学启发的神经网络，可以解决监督学习任务并遵守由一般非线性偏微分方程描述的任何给定物理定律。在第二部分中，作者重点讨论了基于数据驱动的偏微分方程发现问题。根据可用数据是散布在时空中还是以固定的临时快照排列，作者引入了两种主要的算法类别，即连续时间模型和离散时间模型。通过一系列数学物理学基准问题的测试，包括守恒定律、不可压缩流体流动和非线性浅水波的传播等，作者展示了这种方法的有效性。

3.Numerical Gaussian processes for time-dependent and nonlinear partial differential equations

用于时变和非线性偏微分方程的数值高斯过程

「简述：」这篇文章介绍了一种新的方法，叫做数值高斯过程，用于解决时间依赖和非线性偏微分方程。通过将高斯过程（一种机器学习方法）与时间离散化的偏微分方程相结合，能够处理噪声数据和不确定性，避免了对方程求解器的空间离散化需求，并且能够从观察到的数据中学习并逼近潜在解。作者通过几个基准问题展示了该方法的有效性和准确性，并能够处理长时间积分的情况。

基于 PINN

1.Physics‐informed neural networks with monotonicity constraints for Richardson‐Richards equation: Estimation of constitutive relationships and soil water flux density from volumetric water content measurements

Richardson-Richards方程的单调约束物理神经网络

「简述：」本文介绍了一种物理学启发神经网络(PINN)框架，用于解决Richardson-Richards方程的逆问题和仅基于体积含水量测量估计水保留曲线(WRCs)和水导电性函数(HCFs)。该框架不需要初始和边界条件，这些条件在实际应用中很少可用。PINN由三个连接的前馈神经网络组成，其中两个被限制为单调函数以反映WRCs和HCFs的单调性。经过训练的PINN能够重建真实的VWC动力学，并可以以非参数形式恢复底层的WRCs和HCFs。

• 2.A derivative-free method for solving elliptic partial differential equations with deep neural networks.

• 3.PPINN: Parareal physics-informed neural network for time-dependent PDEs

• 4.Solving differential equations using deep neural networks

• 5.Reduced-order modeling of subsurface multiphase flow models using deep residual recurrent neural networks.

• 6.Adaptive activation functions accelerate convergence in deep and physics-informed neural networks

• 7.Locally adaptive activation functions with slope recovery for deep and physics-informed neural networks

可测量标签数据

1.Deep learning of subsurface flow via theory-guided neural network

基于理论指导的神经网络对地下流的深度学习

「简述：」论文提出了一种叫做TgNN的神经网络，它结合了理论指导（如物理方程和其他约束）和数据驱动的学习。TgNN在训练时使用已有的观测数据或模拟数据，同时也接受理论的引导。相比普通的ANN，TgNN可以提供更符合物理规律的预测，并且能更好地泛化到训练数据之外的情况。此外，TgNN模型还在更复杂的场景下进行了测试，如改变边界条件的预测、从噪声数据或异常值中学习、转移学习以及工程控制。数值结果表明，由于物理/工程约束的存在，TgNN模型在预测性、可靠性和通用性方面比ANN模型要好得多。

• 2.Theory-guided auto-encoder for surrogate construction and inverse modeling

• 3.Ensemble neural networks (ENN): A gradient-free stochastic method

• 4.Theory-guided hard constraint projection (HCP): A knowledge-based data-driven scientific machine learning method

3、物理驱动（纯物理约束）

全连接神经网络 (FC-NN)

1.Efficient training of physics‐ informed neural networks via importance sampling

通过重要性采样对物理知识神经网络进行高效训练

「简述：」本文研究了一种重要性采样方法，用于提高物理信息神经网络（PINNs）的训练效率。通过数值示例和理论证据，我们发现在每个训练迭代中，根据与损失函数成比例的分布采样配置点可以改善PINNs训练的收敛行为。此外，我们还发现为更快的重要性采样提供分段常数近似损失函数可以进一步提高训练效率。这种方法简单易行，易于实现，并且不需要引入新的超参数进行校准。

• 2.Deep least-squares methods: An unsupervised learning-based numerical method for solving elliptic PDEs

• 3.Surrogate modeling for fluid flows based on physics-constrained deep learning without simulation data

CNN 求解偏微分方程

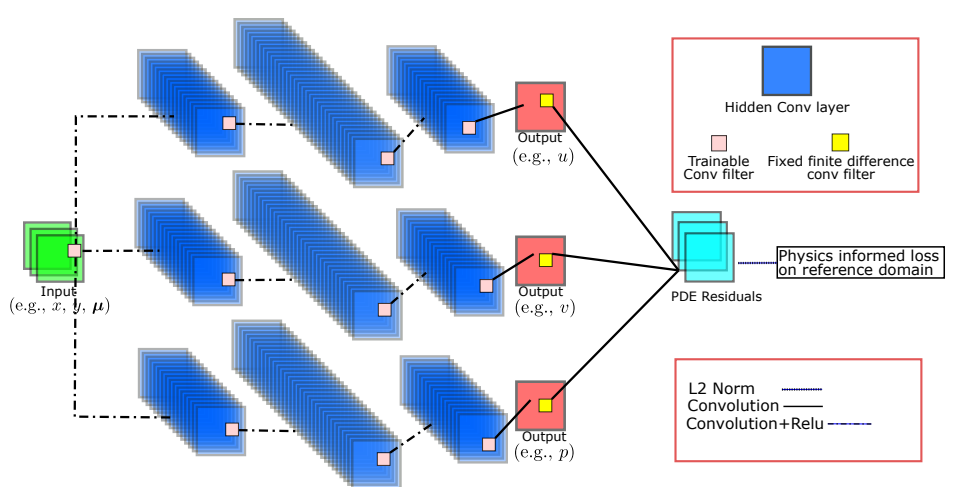
1.PhyGeoNet: Physics-informed geometry-adaptive convolutional neural networks for solving Parameterized Steady-State PDEs on irregular domain

用于求解不规则域上的参数化稳定状态PDE的物理信息几何自适应卷积神经网络。

「简述：」本文提出了一种基于卷积神经网络（CNN）的物理知识神经网络（PINN），用于高效求解不规则域上的参数化偏微分方程（PDEs），无需任何标记数据。通过引入椭圆坐标映射，实现了不规则物理域和规则参考域之间的坐标转换，从而利用了强大的经典CNN主干网络。数值实验表明，该方法在效率和准确性上优于目前最先进的基于全连接神经网络的PINN，可用于解决具有参数化边界条件、可变几何形状和空间变化源场的稳态PDE。

• 2.Bayesian deep convolutional encoder – decoder networks for surrogate modeling and uncertainty quantification

• 3.DenseNet: implementing efficient convent descriptor pyramids

• 4.Physics-constrainedb deep learning for high-dimensional surrogate modeling and uncertainty quantification without labeled data

 

关注下方《学姐带你玩AI》🚀🚀🚀

回复“偏微分方程”获取全部论文+开源代码

码字不易，欢迎大家点赞评论收藏