跳转汇总链接
👉🔗算法题汇总链接
1.1 乘积为正数的最长子数组长度
🔗题目链接
给你一个整数数组 nums ,请你求出乘积为正数的最长子数组的长度。
一个数组的子数组是由原数组中零个或者更多个连续数字组成的数组。
请你返回乘积为正数的最长子数组长度。
在写代码前,务必先做好这五步!梳理清楚思路,写代码只是顺手的事儿,这是第一道题,所以会详细描述分析方法,后面的题也是同一个流程~
- 状态表示:
- 本题得需要两个 dp 表,这里做 f 表和 g 表(设两个表不是一开始就能看出来的,是分析后得出的。先按照题意设一个记录乘积为正数的的最长子数组的长度 f 表,后面在分析正负数情况的时候发现还需要一个记录负数的,于是增添了 g 表)
- f[i] 表示:以 i 位置元素为结尾乘积为正数的最长子数组的长度
- g[i] 表示:以 i 位置元素为结尾乘积为负数的最长子数组的长度
- 状态转移方程:
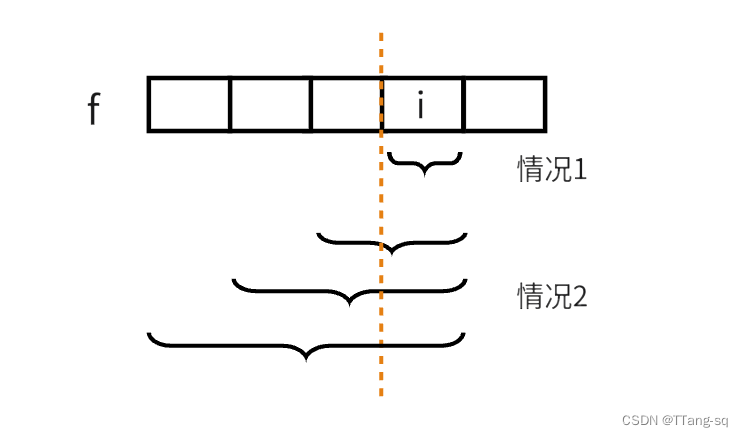
- 分析 f:首先将“子数组乘积为正数”中的“子数组”,分为自身和自身+之前的解,按照题意分为长度为1或者长度大于1,可以分析状态转移方程(如下)

- 原本需要分成这两类,是因为一般会取 max(自身,自身+之前的解) 或是 min(自身,自身+之前的解),但是这道题我们可以观察到,列出来的方程中 nums[i] 符号相同时的情况可以覆盖另一个,所以方程可以简单写成如下。

- 原本需要分成这两类,是因为一般会取 max(自身,自身+之前的解) 或是 min(自身,自身+之前的解),但是这道题我们可以观察到,列出来的方程中 nums[i] 符号相同时的情况可以覆盖另一个,所以方程可以简单写成如下。
- g 表的分析同理。

- 分析 f:首先将“子数组乘积为正数”中的“子数组”,分为自身和自身+之前的解,按照题意分为长度为1或者长度大于1,可以分析状态转移方程(如下)
- 初始化:
- 涉及到 -1 的位置可能在填表的时候越界,这里选用在表的首部多加一个空格的方式防止越界,初始化内容为 0,不会影响后续表的填写。
- 填表顺序:
- 从左往右,两张表一起填。
- 返回值:
- f 表里的最大值。
🐎代码如下:
class Solution {
public:int getMaxLen(vector<int>& nums) {// 1. 创建 dp 表int n = nums.size();vector<int> f(n + 1); // 乘积为正数的最长数auto g = f; // 乘积为负数的最长数// 2. 初始化int fmax = 0;f[0] = g[0] = 0;// 3. 誊写状态转移方式for(int i = 1; i < n + 1; i++){if(nums[i - 1] > 0){f[i] = f[i-1] + 1;g[i] = g[i-1] == 0 ? 0 : g[i-1] + 1;}else if(nums[i - 1] < 0){f[i] = g[i-1] == 0 ? 0 : g[i-1] + 1;g[i] = f[i-1] + 1;}fmax = max(fmax, f[i]);}// 4. 返回值return fmax;}
};
🥰如果本文对你有些帮助,欢迎👉 点赞 收藏 关注,你的支持是对作者大大莫大的鼓励!!(✿◡‿◡) 若有差错恳请留言指正~~