654. 最大二叉树

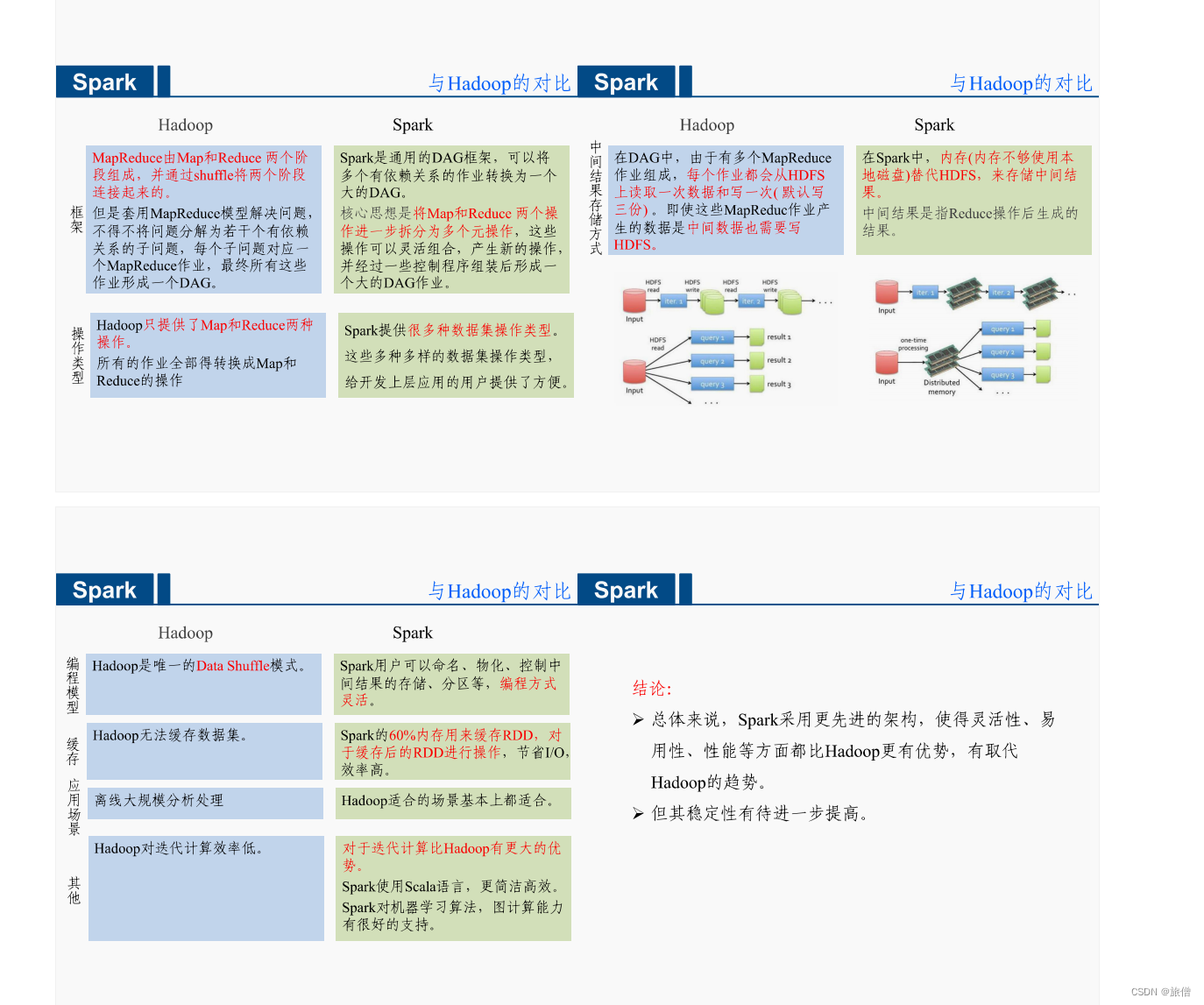
核心：记住递归三部曲，一般传入的参数的都是题目给好的了！把构造树类似于前序遍历一样就可！就是注意单层递归的逻辑！

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:# 递归三部曲if not nums:return max_ = max(nums)max_index = nums.index(max_)root = TreeNode(max_)root.left = self.constructMaximumBinaryTree(nums[:max_index])root.right = self.constructMaximumBinaryTree(nums[max_index + 1:])return rootdef constructMaximumBinaryTree2(self, nums: List[int]) -> Optional[TreeNode]:# 递归的三部曲 1.确定参数以及返回值--传入数组，输出节点 2.结束递归条件--如果数组len==1说明遍历到叶子节点了 3.单层逻辑--找到最大值以及最大值的下标if len(nums) == 1:return TreeNode(nums[0]) node = TreeNode(0)max_numb = 0max_index = 0  for i in range(len(nums)):if nums[i] > max_numb:max_index = imax_numb = nums[i]node.val = max_numb# 判断下标值是否大于0 说明是否有左子树if max_index > 0:new_list = nums[:max_index]node.left = self.constructMaximumBinaryTree(new_list)if max_index < len(nums) - 1:new_list = nums[max_index + 1:]node.right = self.constructMaximumBinaryTree(new_list)return node

617. 合并二叉树

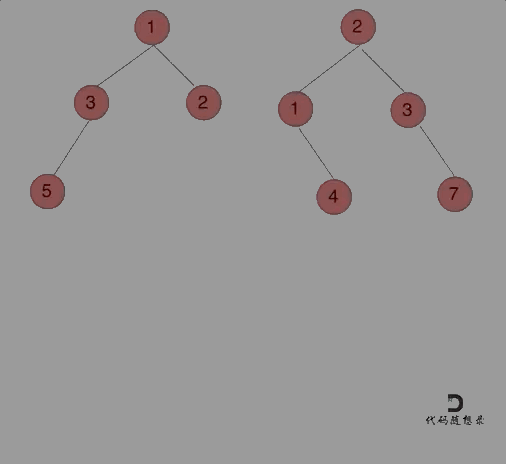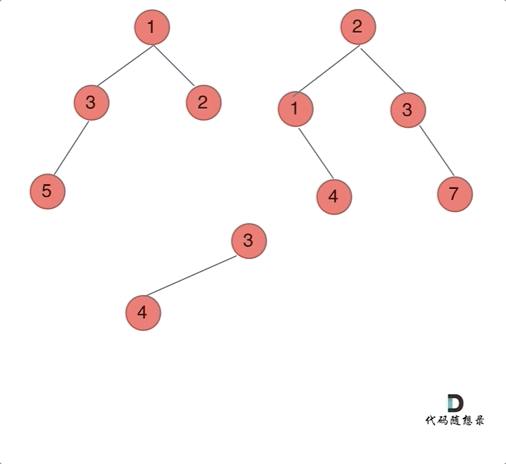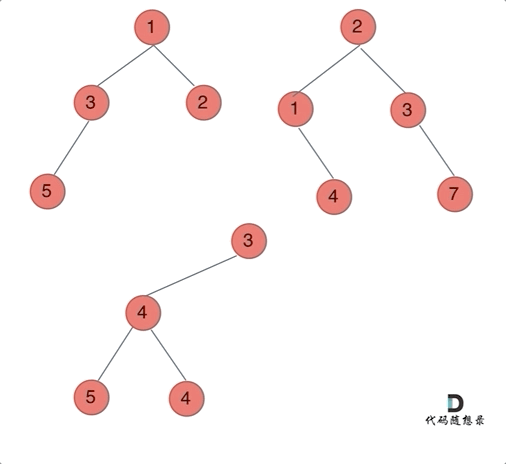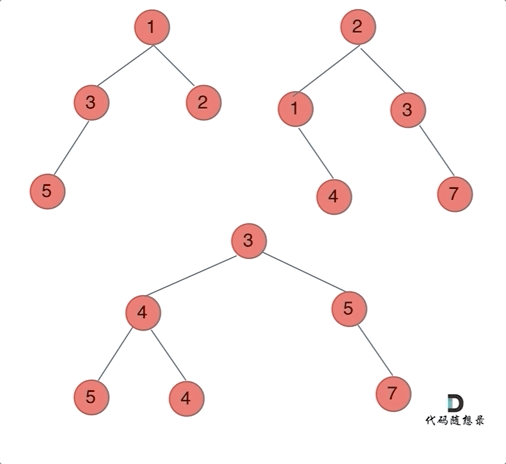
思路：以建立的节点为标准，类似于前缀【中后序】遍历进行构造！或者使用迭代法【建立两个队列进行维护就好了】

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:# 终止条件：但凡有一个节点为空，就返回另一个节点，如果另一个也为None就直接返回None# 以创建的新节点为移动标准if not root1:return root2if not root2:return root1node  = TreeNode()node.val = root1.val + root2.valnode.left = self.mergeTrees(root1.left, root2.left)node.right = self.mergeTrees(root1.right, root2.right)return nodedef mergeTrees1(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:if not root1 and not root2:return node = TreeNode(0)if root1 and root2:node.val = root1.val + root2.valnode.left = self.mergeTrees(root1.left,root2.left)node.right = self.mergeTrees(root1.right, root2.right)elif root1 and not root2:node.val = root1.valnode.left = self.mergeTrees(root1.left,None)node.right = self.mergeTrees(root1.right,None)else:node.val = root2.valnode.left = self.mergeTrees(None,root2.left)node.right = self.mergeTrees(None,root2.right)return node

700. 二叉搜索树中的搜索

思想：使用层次遍历或者使用递归或迭代

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
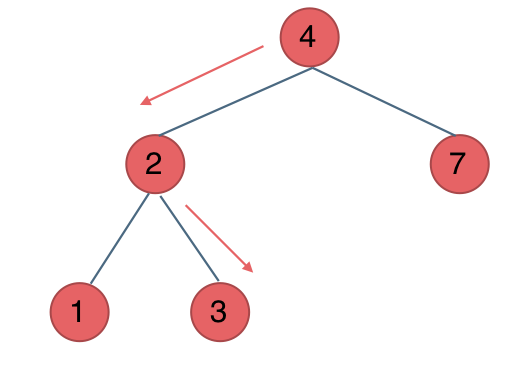
class Solution:# 层次遍历def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:queue_1 = []if not root:# return queue_1.append(root) 犯下了致命弱智的错误return Nonequeue_1.append(root)while len(queue_1) > 0:node = queue_1.pop(0)if node.val == val:return nodeif node.left:queue_1.append(node.left)if node.right:queue_1.append(node.right)return None# 迭代法def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:while root:if root.val > val:root = root.leftelif root.val < val:root = root.rightelse:return rootreturn None# 递归法def searchBST(self, root: TreeNode, val: int) -> TreeNode:# 为什么要有返回值: #   因为搜索到目标节点就要立即return，#   这样才是找到节点就返回（搜索某一条边），如果不加return，就是遍历整棵树了。if not root or root.val == val: return rootif root.val > val: return self.searchBST(root.left, val)if root.val < val: return self.searchBST(root.right, val)

98. 验证二叉搜索树

核心：理解中序遍历的规则，在二叉树中中序遍历出来的结果一定是有序的！

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
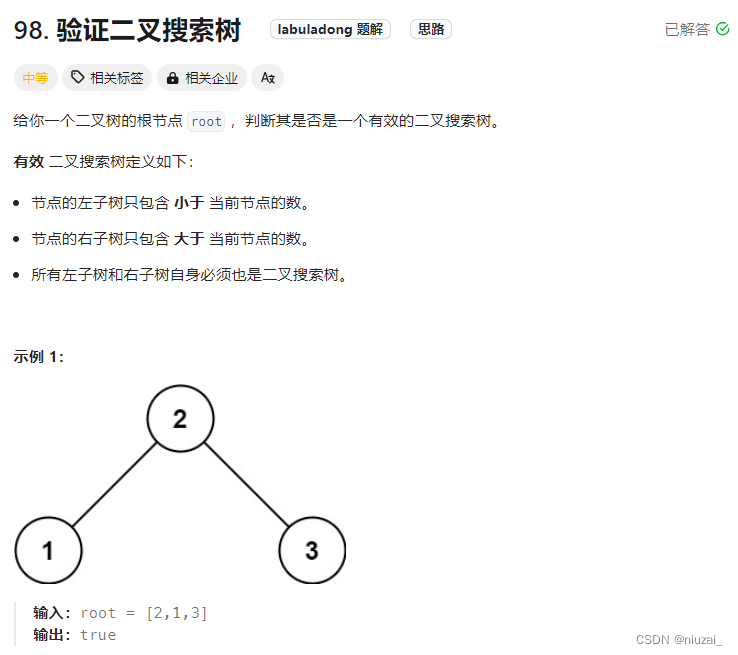
class Solution:def __init__(self):self.nums = []def isValidBST(self, root: Optional[TreeNode]) -> bool:# 中序遍历出来的数一定是有序的self.nums = []  # 清空数组self.traversal(root)for i in range(1, len(self.nums)):# 注意要小于等于，搜索树里不能有相同元素if self.nums[i] <= self.nums[i - 1]:return Falsereturn Truedef traversal(self, root):if root is None:returnself.traversal(root.left)self.nums.append(root.val)  # 将二叉搜索树转换为有序数组self.traversal(root.right)# 设置最小值比较，就可以修改了单层逻辑那个地方，左了一个比较！
class Solution:def __init__(self):self.maxVal = float('-inf')  # 因为后台测试数据中有int最小值def isValidBST(self, root):if root is None:return Trueleft = self.isValidBST(root.left)# 中序遍历，验证遍历的元素是不是从小到大if self.maxVal < root.val:self.maxVal = root.valelse:return Falseright = self.isValidBST(root.right)return left and right