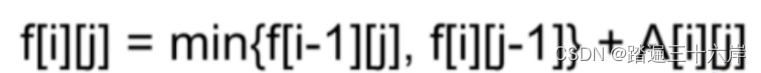在计算机刚刚诞生的年代,计算机是一种只有天才才能掌握的工具。人们对软件的认知仅仅停留在程序的层面上,所谓的软件开发就是那些能够掌握计算机的天才们写的一些只有计算机才能理解的二进制序列。但随着技术的发展,软件的复杂度不断提高,人们进入了大规模软件开发的时代。这时,人们发现,软件系统已经变得非常复杂,需要遵循一定的开发方法才能取得成功,于是称这些模式化的开发方法为开发模型。
一、瀑布模型
顾名思义,瀑布模型就如同瀑布一样,从一个特定的阶段流向下一个阶段,如图 6-1所示。
1.瀑布模型的核心思想
瀑布模型认为,软件开发是一个阶段化的精确的过程。就像要制造一艘航空母舰,首先需要知道航空母舰的参数(长、宽、高、排水量、航速等)。在这些参数的技术上需要对航空母舰进行设计,设计包括总体设计和详细设计。只有设计得一清二楚的图纸才能交付施工,否则造出的零件肯定拼装不到一起。制造完毕后,要把这些零件一个一个地拼装起来,拼装成发动机、船舱等部分,并检查这些部分是否符合设计标准,这就是集成测试。最后,把各个部分组合在一起,造出一艘巨大的航母。软件要经过需求分析、总体设计、详细设计、编码、调试、集成测试和系统测试阶段才能够被准确地实现。在图 6-1 中,每一阶段都有回到前一阶段的反馈线,这指的是,在软件开发中当在后续阶段发现缺陷的时候,可以把这个缺陷反馈到上一阶段进行修正。

从图 6-1 中可以看出瀑布模型的一个重要特点:软件开发的阶段划分是明确的,一个阶段到下一个阶段有明显的界线。在每个阶段结束后,都会有固定的文档或源程序流入下一阶段。在需求分析阶段结束后,需要有明确的描述软件需求的文档;总体设计结束后,需要有描述软件总体结构的文档;详细设计结束后,需要有可以用来编码的详细设计文档;而编码结束后,代码本身被作为文档流到下一个阶段。因此也称瀑布模型是面向文档的软件开发模型。
当软件需求明确、稳定时,可以采用瀑布模型按部就班地开发软件,当软件需求不明确或变动剧烈时,瀑布模型中往往要到测试阶段才会暴露出需求的缺陷,造成后期修改代价太大,难以控制开发的风险。
二、瀑布 V 模型
瀑布 V 模型是瀑布模型的一种变体。随着对瀑布模型的应用,人们发现,缺陷是无法避免的,任何一个阶段都会在软件中引入缺陷,而最后的测试也不能保证软件完全没有缺陷,只能争取在交付前发现更多的缺陷。测试成为软件开发中非常重要的环节,测试的质量直接影响到软件的质量。因此,人们对瀑布模型进行了小小的更改,提出了更强调测试的瀑布 V 模型,如图 6-2 所示。

整个瀑布模型在编码与调试阶段转了个弯,形成了一个对称的 V 字。瀑布 V 模型同标准瀑布模型一样,在进行完需求分析后就将进入总体设计阶段,但是除总体设计外,需求分析还有一条虚线指向系统测试。这指的是,需求分析的结果将作为系统测试的准则,即需求分析阶段也将产生同软件需求一致的系统测试;同时软件产品是否符合最初的需求将在系统测试阶段得到验证。以此类推,总体设计对应了集成测试,详细设计对应了单元测试。瀑布 V 模型不但保持了瀑布模型的阶段式文档驱动的特点,而且更强调了软件产品的验证工作。
瀑布模型的缺点
虽然是经典的开发模型,但瀑布模型中仍存在一些难以克服的缺陷,即使是在改进的瀑布 V 模型中还是会存在。
首先,在瀑布模型中,需求分析阶段是一切活动的基础,设计、实现和验证活动都是从需求分析阶段的结果导出的。一旦需求分析的结果不完全正确,存在偏差,那么后续的活动只能放大这个偏差,在错误的道路上越走越远。事实上,由于用户和开发者的立场、经验、知识域都不相同,不同的人对同一件事物的表述也不同,这就造成需求分析的结果不可能精确、完整地描述整个软件系统。所以瀑布模型后期的维护工作相当繁重,而这些维护工作大多都是修正在需求分析阶段引入的缺陷。这个问题是瀑布模型难以克服的。
其次,瀑布模型难以适应变化。在瀑布模型中精确地定义了每一个阶段的活动和活动结果,而每一阶段都紧密依赖于上一阶段的结果。如果在软件的后期出现了需求的变化,整个系统又要从头开始。
再次,使用瀑布模型意味着当所有阶段都结束才能最终交付软件产品,所以在提出需求后需要相当长一段时间的等待才能够看到最终结果,才能发现软件产品究竟能不能够满足客户的需求。
最后,文档驱动型的瀑布模型除了制造出软件产品外还将产生一大堆的文档,大部分的文档对客户没有任何意义,但完成这些对客户没有意义的文档却需要花费大量的人力。所以瀑布模型也是一种重载过程。
三、演化模型
瀑布模型看起来很好,随着一个又一个阶段的流过,软件系统就被建立起来了。可是在应用软件开发的过程中,人们发现很难一次性完全理解用户的需求、设计出完美的架构,开发出可用的系统,这是由于人的认知本身就是一个过程,这个过程是渐进的、不断深化的。对于复杂问题,“做两次”肯定能够做得更好。那么,对于软件开发这个复杂而且与人的认知过程紧密相关的事也应该是一个渐进的过程。
演化模型正是基于这个观点提出的。一般情况下,一个演化模型可以看做若干次瀑布模型的迭代,当完成一个瀑布模型后,重新进入下一个迭代周期,软件在这样的迭代过程中得以演化、完善。根据不同的迭代特点,演化模型可以演变为螺旋模型、增量模型和原型法开发。
四、螺旋模型
螺旋模型将瀑布模型和演化模型结合起来,不仅体现了两个模型的优点,而且还强调了其他模型均忽略了的风险分析。螺旋模型的每一周期都包括需求定义、风险分析、工程实现和评审 4 个阶段,由这 4 个阶段进行迭代,软件开发过程每迭代一次,软件开发就前进一个层次。采用螺旋模型的软件过程如图 6-3 所示。
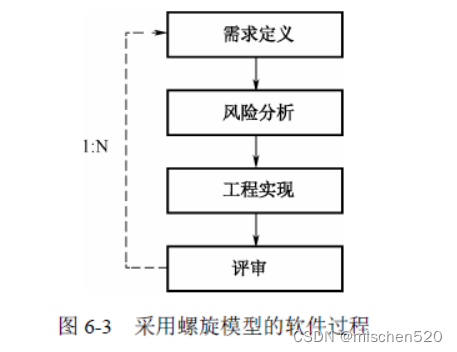
螺旋模型的基本做法是在“瀑布模型”的每一个开发阶段前,引入一个非常严格的风险识别、风险分析和风险控制。它把软件项目分解成一个个小项目,每个小项目都标识一个或多个主要风险,直到所有的主要风险因素都被确定。
螺旋模型强调风险分析,使得开发人员和用户对每个演化层出现的风险都有所了解,继而做出应有的反应。因此,螺旋模型特别适用于庞大而复杂、具有高风险的系统,对于这些系统,风险是软件开发潜在的、不可忽视的不利因素,它可能在不同程度上损害软件开发过程,影响软件产品的质量。减小软件风险的目标是在造成危害之前,及时对风险进行识别、分析,决定采取何种对策,进而消除或减少风险的损害。
与瀑布模型相比,螺旋模型支持用户需求的动态变化,为用户参与软件开发的所有关键决策提供了方便,有助于提高目标软件的适应能力,为项目管理人员及时调整管理决策提供了便利,从而降低了软件开发风险。
但是,不能说螺旋模型绝对比其他模型优越,事实上,螺旋模型也有其自身的缺点:
(1)采用螺旋模型,需要具有相当丰富的风险评估经验和专业知识。在风险较大的项目开发中,如果未能及时标识风险,势必会造成重大损失。
(2)过多的迭代次数会增加开发成本,延迟提交时间。
五、增量模型
演化模型的另一种形式是增量模型。在系统的技术架构成熟、风险较低的时候,可以采用增量的方式进行系统开发,这样可以提前进行集成测试和系统测试,缩短初始版本的发布周期,提高用户对系统的可见度。
对于增量模型,通常有两种策略。一是增量发布的办法。即首先做好系统的分析和设计工作,然后将系统划分为若干不同的版本,每一个版本都是一个完整的系统,后一版本以前一版本为基础进行开发,扩充前一版本的功能。在这种策略中,第一版本往往是系统的核心功能,可以满足用户最基本的需求,随着增量的发布,系统的功能逐步地丰富、完善起来。用户在很短的时间内就可以得到系统的初始版本并进行试用。试用中的问题可以很快地反馈到后续开发中,从而降低了系统的风险。在应用增量模型中需要注意:
(1)每一个版本都是一个完整的版本。虽然最初的几个增量不能完全地实现用户需求,但这些版本都是完整的、可用的。
(2)版本间的增量要均匀,这一点是很重要的。如果第一个版本花费一个月的时间,而第二个版本需要花费 6 个月的时间,这种不均匀的分配会降低增量发布的意义,需要重新调整。
另一种策略是原型法。同增量发布不同,原型法的每一次迭代都经过一个完整的生命周期。当用户需求很不明确或技术架构中存在很多不可知因素的时候,可以采用原型法。在初始的原型中,针对一般性的用户需求进行快速实现,并不考虑算法的合理性或系统的稳定性。这个原型的主要目的是获得精确的用户需求,或验证架构的可用性。一般情况下,会在后面的开发中抛弃这个原型,重新实现完整的系统。
六、构件组装模型
随着软构件技术的发展,人们开始尝试利用软构件进行搭积木式的开发,即构件组装模型。在构建组装模型中,当经过需求分析定义出软件功能后,将对构件的组装结构进行设计,将系统划分成一组构件的集合,明确构件之间的关系。在确定了系统构件后,则将独立完成每一个构件,这时既可以开发软件构件,也可以重用已有的构件,当然也可以购买或选用第三方的构件。构件是独立的、自包容的,因此架构的开发也是独立的,构件之间通过接口相互协作。
构件组装模型的一般开发过程如图 6-4 所示。

构件组装模型的优点如下:
(1)构件的自包容性让系统的扩展变得更加容易
(2)设计良好的构件更容易被重用,降低软件开发成本
(3)构件的粒度较整个系统更小,因此安排开发任务更加灵活,可以将开发团队分成若干组,并行地独立开发构件。
鱼与熊掌不可兼得,构件组装模型也有明显的缺点:
(1)对构件的设计需要经验丰富的架构设计师,设计不良的构件难以实现构件的优点,降低构件组装模型的重用度。
(2)在考虑软件的重用度时,往往会对其他方面做出让步,如性能等。
(3)使用构件组装应用程序时,要求程序员熟练地掌握构件,增加了研发人员的学习成本。
(4)第三方构件库的质量会最终影响到软件的质量,而第三方构件库的质量往往是开发团队难以控制的。
软件开发模型(架构师复习资料)
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.rhkb.cn/news/220454.html
如若内容造成侵权/违法违规/事实不符,请联系长河编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
安装android studio
记录一下安装android studio的过程:
1.首先安装android studio到某一文件夹后,在C盘用户目录下可以看到.android文件夹。C:\Users\22515\AppData\Local\Google目录下也会出现AndroidStudio2022.2文件夹。(注意:用户名,…
算法通关第十九关-青铜挑战理解动态规划
大家好我是苏麟 , 今天聊聊动态规划 . 动态规划是最热门、最重要的算法思想之一,在面试中大量出现,而且题目整体都偏难一些对于大部人来说,最大的问题是不知道动态规划到底是怎么回事。很多人看教程等,都被里面的状态子问题、状态…
maui中实现加载更多 RefreshView跟ListView(2)
一个类似商品例表的下拉效果:
代码
新增个类为商品商体类 public class ProductItem{public string ImageSource { get; set; }public string ProductName { get; set; }public string Price { get; set; }}界面代码:
<?xml version"1.0&quo…
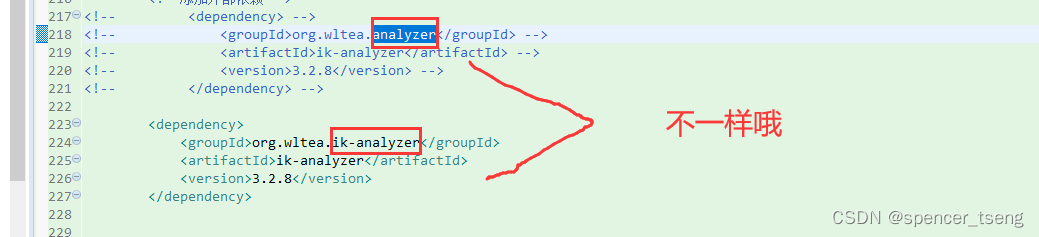
Missing artifact org.wltea.analyzer:ik-analyzer:jar:5.0
没有找到【org.wltea.analyzer】
找到了【org.wltea.ik-analyzer】 https://github.com/wks/ik-analyzer https://github.com/wks/ik-analyzer.git
https://code.google.com/archive/p/ik-analyzer/downloads?page2 C:\Users\Administrator\Desktop\ik-analyzer-master>m…
IDEA添加Apifox插件后,返回参数不详细解决办法
Apifox官方文档地址(文档中返回的是特殊情况,跟我现在项目的返回不一样,因此需要更改配置) 点击跳转到官方API地址 实现步骤分为两步:第一步:添加配置,第二步使用注解。
1.添加配置
打开Idea设置,添加配置…
带你学C语言~指针(2)
目录 🏉前言
🚀 数组名的理解
🚀使用指针访问数组
✈一维数组传参的本质
✈冒泡排序
🏆二级指针
🏆指针数组
🏆指针数组模拟二维数组
🎉结束语 🏉前言
上一章,小…
element组件库的日期选择器如何限制?
本次项目中涉及到根据日期查找出来的数据进行调整,所以修改的数据必须是查找范围内的数据.需要对调整数据的日期进行限制,效果如下: 首先我们使用了element 组件库的日期选择器,其中灌完介绍, picker-options中函数disabledDate可以设置禁用状态,代码如下: <el-date-pickerv…
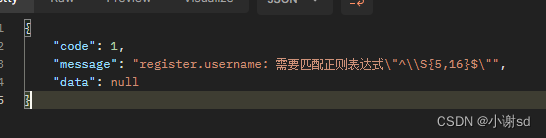
【SpringBoot】参数校验及异常处理
实现注册功能时经常遇到参数校验的问题。 参数校验
引入依赖
<dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-validation</artifactId>
</dependency>参数前添加注解,并指定校验规…
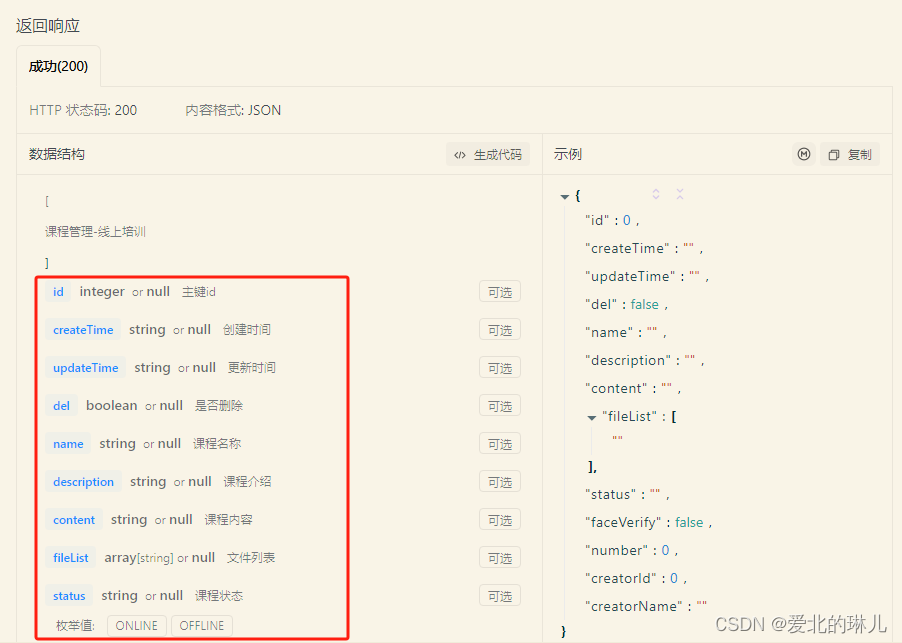
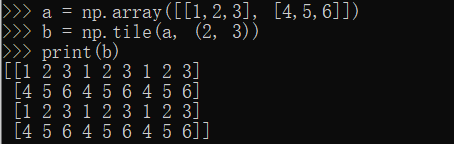
【数据分析之Numpy】Numpy中复制函数numpy.repeat()与numpy.tile()的使用方法及区别
一、简介 numpy.repeat()与numpy.tile()都是Numpy库中的复制函数,用于将数组中的元素重复指定的次数。 numpy.repeat()函数接受三个参数:要重复的数组、重复的次数和重复的轴。 numpy.tile()函数接受两个参数:要重复的数组和重复的次数。
二…
Github 2023-12-18 开源项目周报 Top14
根据Github Trendings的统计,本周(2023-12-18统计)共有14个项目上榜。根据开发语言中项目的数量,汇总情况如下:
开发语言项目数量TypeScript项目4Python项目4Jupyter Notebook项目3非开发语言项目1JavaScript项目1Rust项目1Go项目1
基于项目…
自然语言处理阅读第二弹
HuggingFace
镜像网站模型库
NLP中的自回归模型和自编码模型
自回归:根据上文内容预测下一个可能的单词,或者根据下文预测上一个可能的单词。只能利用上文或者下文的信息,不能同时利用上文和下文的信息。自编码:对输入的句子随…
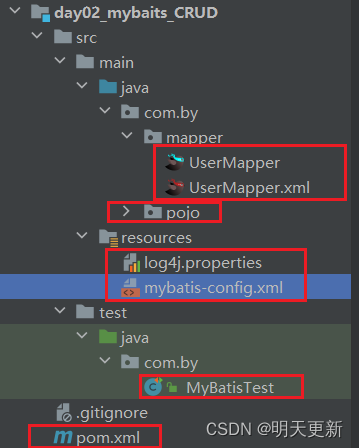
MyBatis的查询方法!!!
准备工作:1.创建一个maven工程,然后将pojo类导入到项目中去。 2.导入依赖到pom.xml文件中 3.在resources中创建log4j.properites和mybatis-config.xml 4.创建UserMapper接口和UserMapper.xml文件 5.创建测试类MyBatisTest
1.创建Maven工程,还…
Windows 安装RocketMQ
1.rocketmq下载 https://archive.apache.org/dist/rocketmq/5.1.4/ 2.环境准备
64位JDK 1.8;
Maven 3.2.x;
64位操作系统系统,本文档在Windows上安装
3.解压到一个无中文无空格的目录下,解压后目录如下: 配置环境变量 4.更改配置
java的…
2018年第七届数学建模国际赛小美赛B题世界杯足球赛的赛制安排解题全过程文档及程序
2018年第七届数学建模国际赛小美赛
B题 世界杯足球赛的赛制安排
原题再现: 有32支球队参加国际足联世界杯决赛阶段的比赛。但从2026年开始,球队的数量将增加到48支。由于时间有限,一支球队不能打太多比赛。因此,国际足联提议改变…
SpringBoot Whitelabel Error Page 报错--【已解决】
springboot 报错信息如下 这个报错页面就是个404 ,代表你访问的url 没有对应的的requestmapping 其实没啥影响的一个问题,但是看到Error 就是不爽,改了他丫的
解决方法如下
一、调整application.properties配置【治标不治本】
server.err…
Cockpit upload文件上传漏洞(CVE-2023-1313)
0x01 产品简介
Cockpit 是一个自托管、灵活且用户友好的无头内容平台,用于创建自定义数字体验。
0x02 漏洞概述
Cockpit assetsmanager/upload接口处存在文件上传漏洞,攻击者可通过该漏洞在服务器端任意上传代码,写入后门,获取服务器权限,进而控制整个web服务器。
0x0…
深入理解 hash 和 history:网页导航的基础(下)
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云…
Linux 特殊符号
目录 1. # 注释
2. ;命令分隔符
3. .. 上级目录
4. . 当前目录
5. " " 换行,解析变量
6. 换行,不解析变量
7. \ 和 /
8. !历史命令调用,取反
9. * 通配符
10. $ 调用变量
11. | 管道
12. ||
…
推荐文章
- 千橡CEO陈一舟5日聊微软入股Facebook和校内网
- 轻量应用服务器:亚马逊云科技打造全球领先的云计算解决方案
- CRM中的大客户销售是什么?
- 软考-高级-系统架构设计师教程(清华第2版)【第18章 安全架构设计理论与实践(P648~690)-思维导图】
- # Redis 入门到精通(一)数据类型(3)
- #A. gzx 的数学题
- (※)力扣刷题-栈和队列-用栈实现队列
- (202302)统计学习方法习题实战TASK2 感知机
- (6)(6.6) 恢复任务回放
- (c语言)经典bug
- (javascript)为什么await在forEach中不生效?
- (React生命周期)前端八股文修炼Day8