簇内平方和表示数据点到其簇内质心的距离的平方和，公式如下：

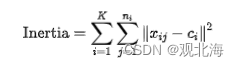
其中， 是k簇数， ni是第 i 个簇的样本数， xij是第  i个簇中的第 j 个样本。

import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs# 生成模拟数据
X, _ = make_blobs(n_samples=300, centers=4, random_state=42)# 尝试不同的簇数，计算簇内平方和
inertia = []
for k in range(1, 11):kmeans = KMeans(n_clusters=k, random_state=42)kmeans.fit(X)inertia.append(kmeans.inertia_)# 绘制肘部法图像
plt.plot(range(1, 11), inertia, marker='o')
plt.xlabel('Number of Clusters (K)')
plt.ylabel('Inertia')
plt.title('Elbow Method for Optimal K')
plt.show()

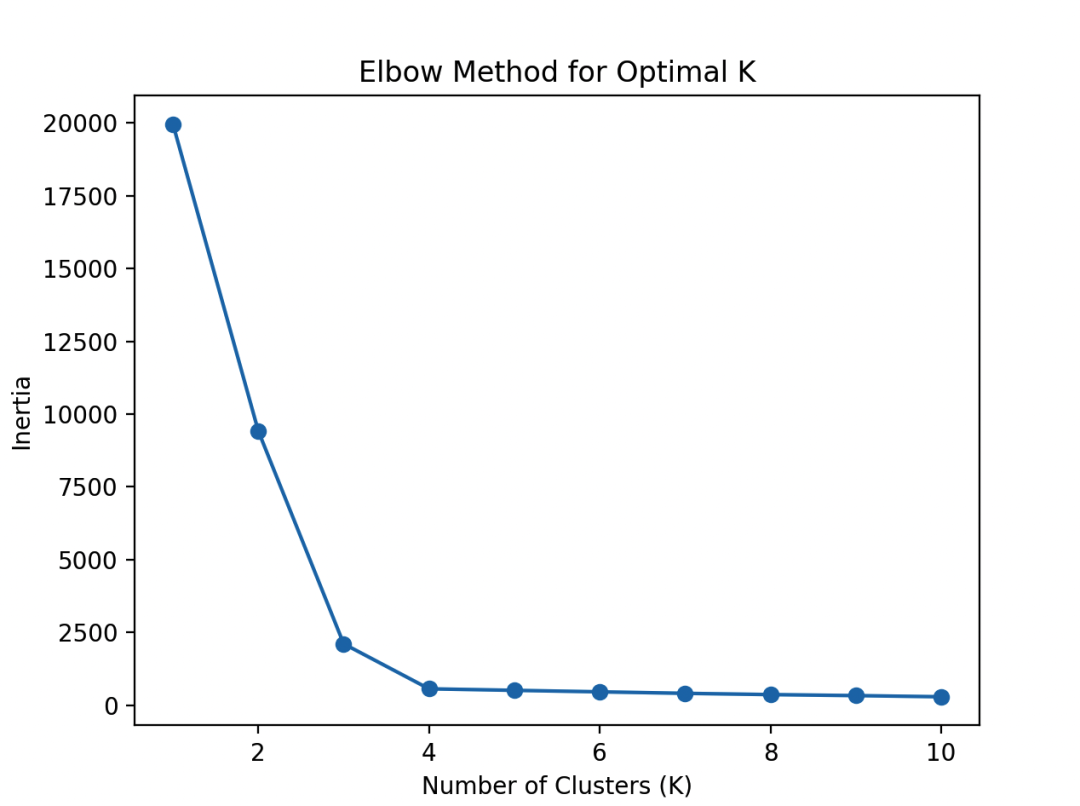
在图像中，我们寻找一个肘部，即簇内平方和的变化趋势减缓的点。这个肘部对应的簇数就是我们的最佳选择。

需要注意，有时候肘部并不明显，这时可能需要结合业务背景和其他评估指标来综合判断最佳的簇数。

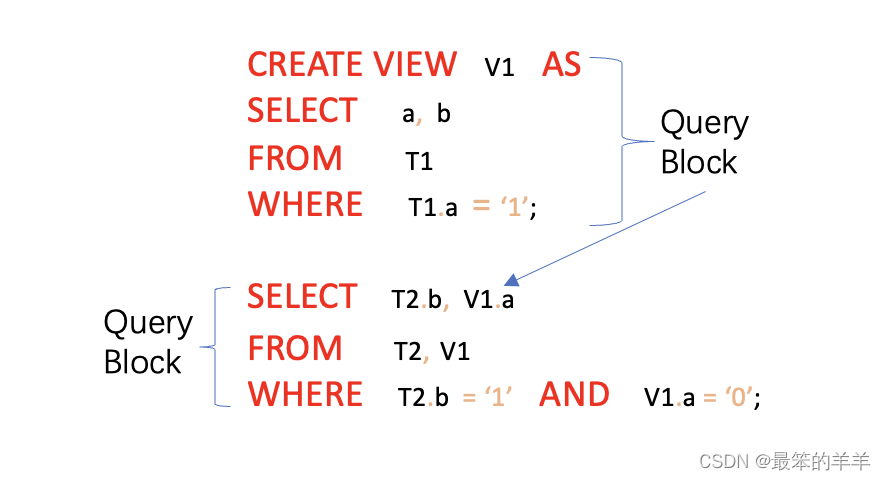
层次聚类的链接方式

层次聚类的链接方式主要有单链接（single-linkage）和完全链接（complete-linkage）两种，它们在形成聚类时有着不同的原理和效果。

1. 单链接 (Single-linkage)：

在单链接中，两个聚类的距离被定义为它们中最近的两个点之间的距离。

也就是说，如果一个簇中的某个点与另一个簇中的所有点的距离都很小，那么这两个簇将会很接近。

2. 完全链接 (Complete-linkage)：

在完全链接中，两个聚类的距离被定义为它们中最远的两个点之间的距离。这意味着两个簇被认为是在它们中最远的点之间保持一致的情况下被连接。

选择方式：

• 如果你的数据可能包含离群点，并且你希望对异常值具有一定的鲁棒性，可以选择完全链接。

• 如果你的数据相对干净，且你希望得到更细致的簇，可以选择单链接。

import numpy as np
from scipy.spatial.distance import pdist, squareform
from scipy.cluster.hierarchy import linkage, dendrogram
import matplotlib.pyplot as plt# 生成一些示例数据
np.random.seed(42)
data = np.random.rand(10, 2)# 计算距离矩阵
distance_matrix = squareform(pdist(data))# 使用单链接层次聚类
single_linkage = linkage(distance_matrix, method='single')# 使用完全链接层次聚类
complete_linkage = linkage(distance_matrix, method='complete')# 绘制树状图
plt.figure(figsize=(12, 6))plt.subplot(1, 2, 1)
dendrogram(single_linkage)
plt.title('Single Linkage')plt.subplot(1, 2, 2)
dendrogram(complete_linkage)
plt.title('Complete Linkage')plt.show()

这段代码使用了scipy库中的linkage和dendrogram函数来进行单链接和完全链接的层次聚类，并绘制了树状图，有助于理解聚类的形成过程。

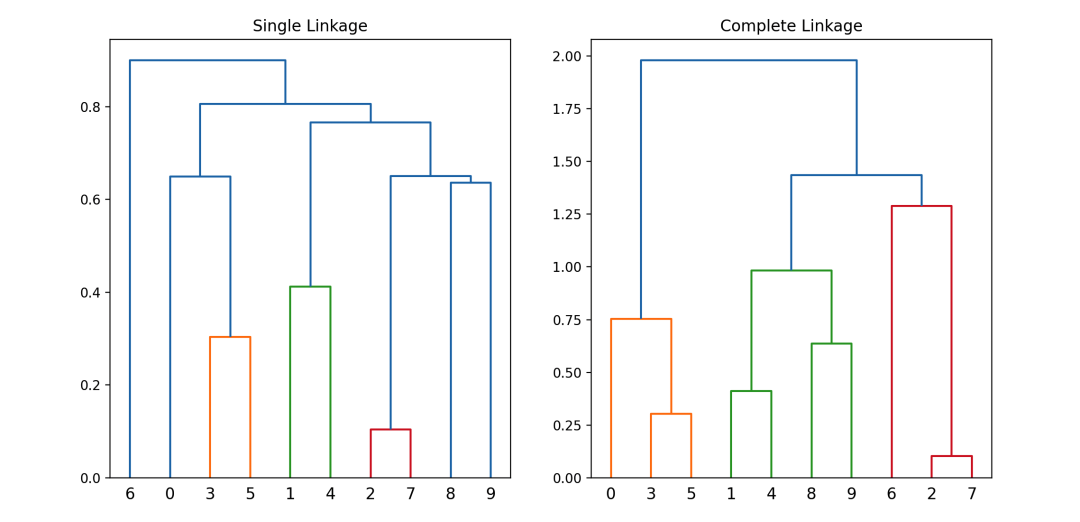
1. 了解数据特性： 首先，你需要了解你的数据集特性，包括样本分布、聚类的密度和大小。不同的数据集可能需要不同的参数设置。

2. 可视化数据： 使用散点图等可视化工具来观察数据的分布，这可以帮助你判断合适的邻域半径和最小样本数。可视化工具可以是matplotlib库，用于绘制数据分布图。

3. 尝试不同参数组合： 通过尝试不同的邻域半径和最小样本数的组合，观察聚类结果的变化。通常，可以通过在一定范围内进行网格搜索来找到最优的参数组合。可以使用嵌套循环来遍历参数空间，然后评估每种组合的聚类效果。

4. 使用密度可视化： 利用DBSCAN的核心思想是根据密度连接点，你可以通过在邻域内绘制样本点的个数来进行密度可视化。这有助于理解在不同参数下的数据密度分布。

下面用PyTorch实现DBSCAN的代码，并用matplotlib画出密度可视化图：

import torch
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
from sklearn.cluster import DBSCAN# 生成一些示例数据
X, _ = make_blobs(n_samples=300, centers=3, cluster_std=0.60, random_state=0)# 转换为PyTorch张量
X_tensor = torch.tensor(X, dtype=torch.float32)# DBSCAN算法
dbscan = DBSCAN(eps=0.3, min_samples=5)
labels = dbscan.fit_predict(X_tensor)# 绘制密度可视化图
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', s=50, edgecolors='k')
plt.title('DBSCAN Clustering')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()

通过调整eps和min_samples参数，你可以观察到不同的聚类效果。密度可视化图能够帮助你更直观地理解不同参数组合下的聚类结果。

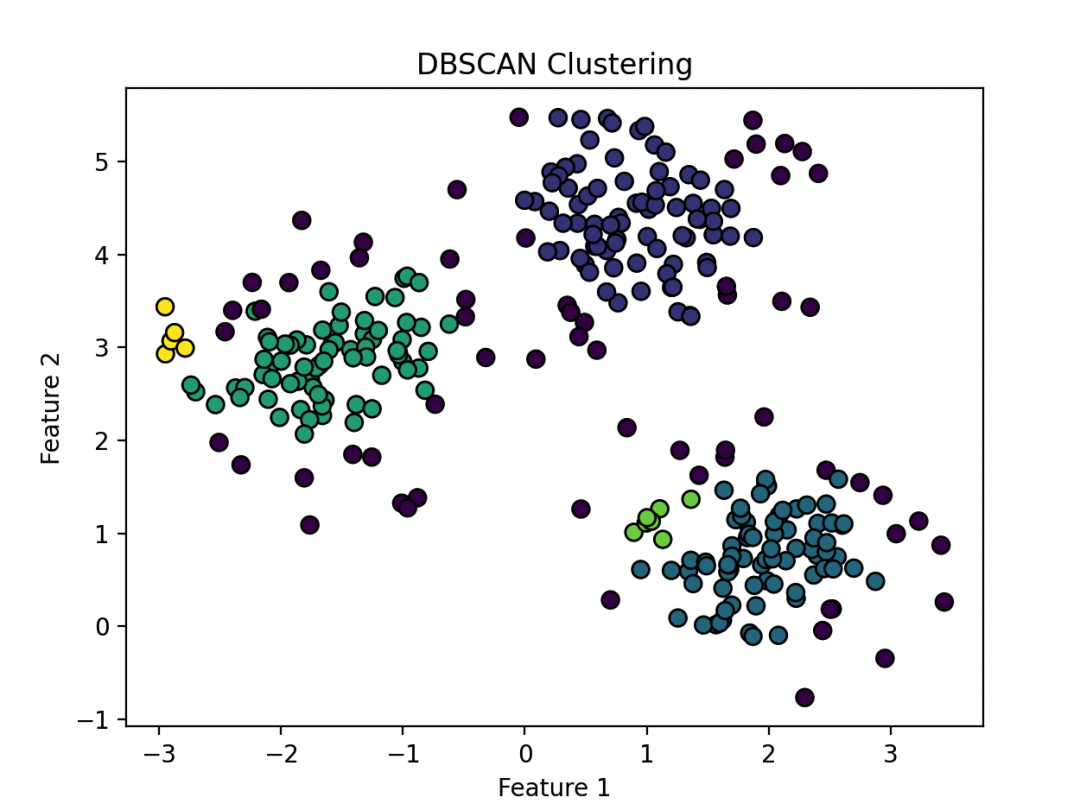
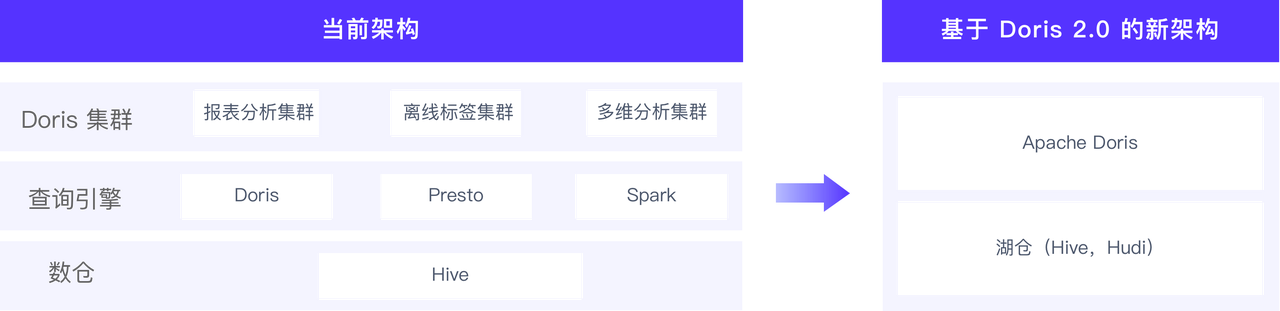
聚类算法的时间复杂度

Mini-Batch K-Means：

K-Means是一种常见的聚类算法，但在大规模数据上运行时可能效率较低。Mini-Batch K-Means是对传统K-Means的一种改进，通过每次随机选取一小部分数据来更新簇中心，从而减少计算量。

可以通过以下步骤实现：

 from sklearn.cluster import MiniBatchKMeanskmeans = MiniBatchKMeans(n_clusters=3, batch_size=100)kmeans.fit(X)

使用近似算法：

对于大规模数据，可以考虑使用一些近似聚类算法，例如K-Means++、K-Means||。这些算法在初始簇中心的选择上更为高效，有助于加速整个聚类过程。

谱聚类：

谱聚类是一种基于图论的聚类方法，可以通过降维来减少计算复杂度。它将数据转换到低维空间，然后在该空间中执行K-Means聚类。在大规模数据集上，通过适当的降维，可以提高计算效率。

 from sklearn.cluster import SpectralClusteringspectral = SpectralClustering(n_clusters=3, affinity='nearest_neighbors')spectral.fit(X)

使用分布式计算：

对于大规模数据，分布式计算是一种有效的方式。可以考虑使用分布式聚类算法，例如Spark中的K-Means。

K-Means并行化：

通过使用多核或GPU进行并行化，可以加速K-Means的计算过程。在Python中，可以使用joblib库来实现多核并行计算。

 from sklearn.cluster import KMeansfrom joblib import parallel_backendwith parallel_backend('threading', n_jobs=2):kmeans = KMeans(n_clusters=3)kmeans.fit(X)

总体而言，在大规模数据上提高聚类算法的计算效率，关键是选择合适的算法、采用近似方法、并行化计算，以及利用分布式计算资源。根据具体问题的性质和数据特点，选择最合适的策略来优化算法的性能。

聚类结果的可解释性

如何更好地解释这些簇对应的数据特征呢

1. 可视化聚类结果： 使用降维技术（如t-SNE、PCA）将高维数据映射到二维或三维空间，然后用不同颜色或标记表示不同的簇。这有助于直观地观察数据点在聚类中的分布。

# 以t-SNE为例
from sklearn.manifold import TSNE
import matplotlib.pyplot as plttsne = TSNE(n_components=2, random_state=42)
clustered_data_tsne = tsne.fit_transform(clustered_data)plt.scatter(clustered_data_tsne[:, 0], clustered_data_tsne[:, 1], c=labels, cmap='viridis')
plt.title('t-SNE Visualization of Clusters')
plt.show()

2. 簇内数据统计： 对每个簇进行统计分析，计算每个簇的中心（均值）、方差等统计量。

可以通过pandas库来实现。

import pandas as pd# 假设data是你的原始数据，labels是聚类结果
clustered_data = pd.DataFrame(data, columns=['feature1', 'feature2', ...])
clustered_data['label'] = labels# 统计每个簇的均值
cluster_means = clustered_data.groupby('label').mean()
print(cluster_means)

3. 特征重要性分析： 对每个簇内数据的特征进行重要性分析，可以使用决策树等模型。这能够帮助你理解哪些特征对于簇的形成起到了重要作用。

from sklearn.tree import DecisionTreeClassifier# 假设X是你的原始数据，y是聚类结果
dt = DecisionTreeClassifier(random_state=42)
dt.fit(X, y)# 特征重要性
feature_importance = dt.feature_importances_
print("Feature Importance:", feature_importance)

4. 关联规则挖掘： 使用关联规则挖掘方法，如Apriori算法，挖掘在同一簇内经常出现的特征组合。

from mlxtend.frequent_patterns import apriori
from mlxtend.frequent_patterns import association_rules# 假设X是你的原始数据，y是聚类结果
frequent_itemsets = apriori(X, min_support=0.5, use_colnames=True)
rules = association_rules(frequent_itemsets, metric="confidence", min_threshold=0.7)
print(rules)

5. 使用主成分分析（PCA）： 对每个簇内的数据应用PCA，找到主成分，以更好地理解簇的结构。

from sklearn.decomposition import PCA# 假设clustered_data是你的聚类结果
pca = PCA(n_components=2)
clustered_data_pca = pca.fit_transform(clustered_data)plt.scatter(clustered_data_pca[:, 0], clustered_data_pca[:, 1], c=labels, cmap='viridis')
plt.title('PCA Visualization of Clusters')
plt.show()

以上方法可以帮助你更好地解释聚类结果，理解每个簇对应的数据特征，进而为进一步分析和应用提供更多的线索。

处理高维数据

下面是一些处理高维数据的方法：

1. 降维技术：

• 主成分分析（PCA）： 通过线性变换将原始高维数据投影到低维空间，保留最大方差的方向，以减少数据的维度。

• t分布邻域嵌入（t-SNE）： 一种非线性降维方法，能够在保持样本之间的相对距离的同时降低维度。

# 使用PCA进行降维
from sklearn.decomposition import PCA# 假设X是高维数据
pca = PCA(n_components=2)
X_low_dim = pca.fit_transform(X)

2. 特征选择：

• 通过选择最相关的特征，剔除冗余信息，从而降低数据的维度。

# 使用方差选择法进行特征选择
from sklearn.feature_selection import VarianceThresholdselector = VarianceThreshold(threshold=0.5)
X_low_dim = selector.fit_transform(X)

3. 使用聚类前的预处理：

• 在应用聚类算法之前，可以先对数据进行预处理，如归一化、标准化，以确保每个维度的重要性相当。

# 使用MinMaxScaler进行归一化
from sklearn.preprocessing import MinMaxScalerscaler = MinMaxScaler()
X_normalized = scaler.fit_transform(X)

4. 密度聚类算法：

• 与基于距离的聚类算法不同，密度聚类算法（如DBSCAN）可以在高维空间中更灵活地发现密集的数据点，而不受维度的影响。

# 使用DBSCAN进行密度聚类
from sklearn.cluster import DBSCANdbscan = DBSCAN(eps=0.5, min_samples=5)
labels = dbscan.fit_predict(X)

5. 集成聚类算法：

• 使用多个聚类算法并集成它们的结果，可以提高在高维数据上的聚类效果。

# 使用KMeans和AgglomerativeClustering进行集成聚类
from sklearn.cluster import KMeans, AgglomerativeClustering
from sklearn.ensemble import VotingClassifierkmeans = KMeans(n_clusters=3)
agg_clustering = AgglomerativeClustering(n_clusters=3)ensemble_clf = VotingClassifier(estimators=[('kmeans', kmeans), ('agg', agg_clustering)], voting='hard')
labels = ensemble_clf.fit_predict(X)

6. 可视化：

• 对降维后的数据进行可视化，以便更好地理解数据的结构和聚类效果。

# 使用matplotlib进行可视化
import matplotlib.pyplot as pltplt.scatter(X_low_dim[:, 0], X_low_dim[:, 1], c=labels, cmap='viridis')
plt.title('Clustering Result in 2D Space')
plt.show()

通过采用这些方法，我们可以更好地处理高维数据上的聚类问题，提高算法的性能和可解释性。