🎬 鸽芷咕：个人主页
 🔥 个人专栏: 《linux深造日志》 《高效算法》

⛺️生活的理想，就是为了理想的生活!

---

📋 前言

  🌈堆排序一个基于二叉堆数据结构的排序算法，其稳定性和排序效率在八大排序中也是名列前茅。
  ⛳️堆我们已经讲解完毕了，今天就来深度了解一下堆排序是怎么实现的以及为什么他那么高效。
  📚本期文章收录在《数据结构&算法》，大家有兴趣可以看看呐！
  ⛺️ 欢迎铁汁们 ✔️ 点赞 👍 收藏 ⭐留言 📝！

一、堆排序的思想概念

堆排序可以说是排序算法中比较高效的了，既稳定又高效。既然叫堆排序那么肯定离不来堆，基于二叉树来进行构建：

• 不知道大家发现过没有堆有一个特性
• 要不就是最大值（大堆）要不然就是一个最小值（小堆）

而我们吧堆顶最大值或最小值进行 pop删除并取出每次的 最大值或者最小值把这些值存储起来

之后他的数据是不是也排序完了，而我们又是用数组来存储的删除不就是把下标 减减吗？

二、堆排序的两种实现方式

堆排序的核心思想就是利用堆的特性来进行数据的取出每次都是最大值或者最小值，那么我得到一组数据要进行堆排序首先：

• 这组数据需要时堆才能进行排序，那么我们就要开始建堆就完了。

建堆的方法一共有俩种分别是向下取整和向上取整这里都给大家介绍一下

2.1 向上取整

向上取整就是，把新的数据尾插到堆里面然后把他和父节点进行对比调整：

• 数组存储这里有一个特点 parent = （child-1）/ 2 ;
• 父节点等于子节点 -1 除二
  

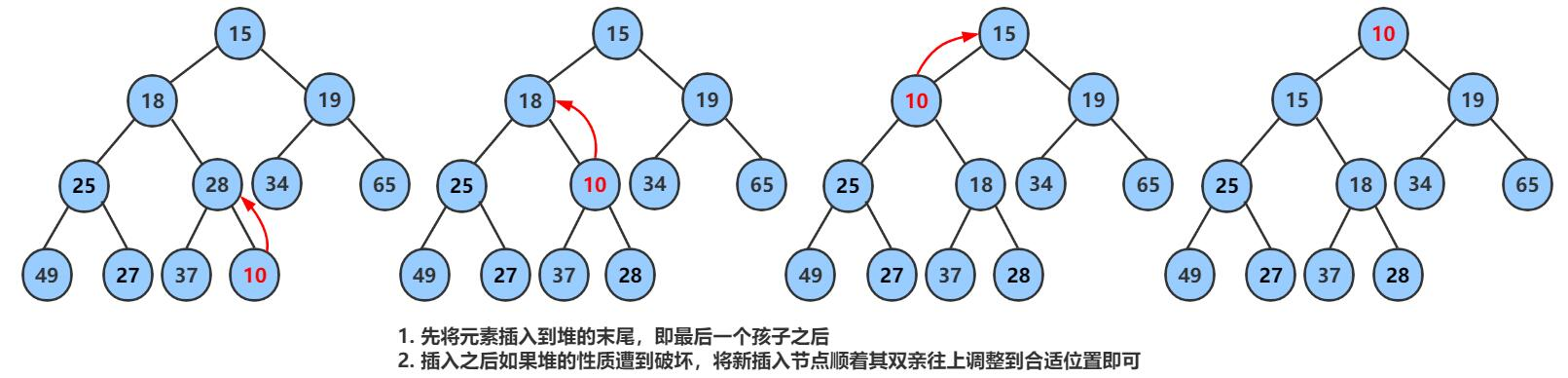
📚 代码演示：

//向上调整
void adjustup(HeapTypeData* a, int child)
{int parent = (child - 1) / 2;while (child > 0){//建小堆if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (parent - 1) / 2;}else{break;}}}

2.2 向下取整

向下取整的思想就是把堆顶数据左右子树的的数值进行对比然后向下进行调整：

• 🔥 向下调整算法有一个前提：左右子树必须是一个堆，才能调整
• 这里由于是数组存储的所以堆的左右子树都是
• child = parent* 2+1;
• 孩子节点的左节点都等于 父节点
  
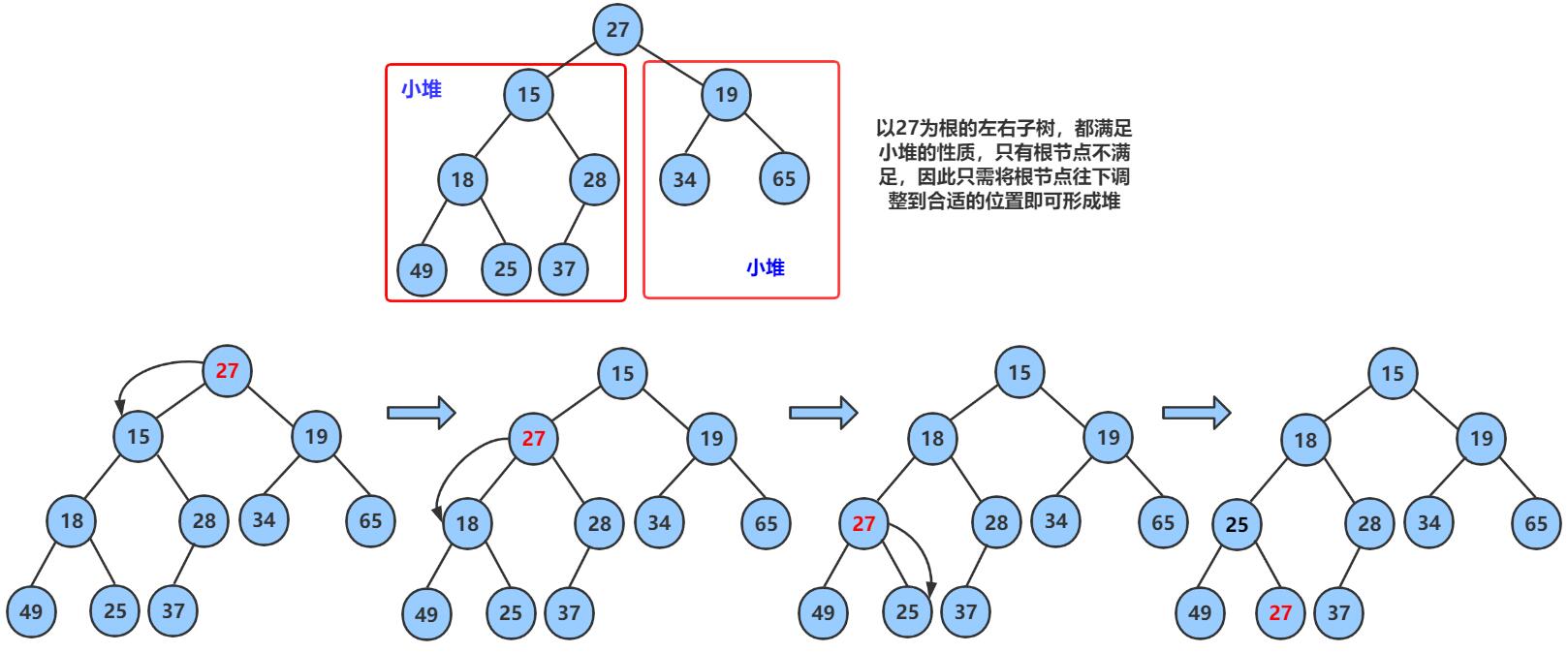
  如果堆顶数据和左右子树对比 ，然后再进行调整数据

📚 代码演示：

//向下调整
void adjustdown(HeapTypeData* a, int n, int parent)
{int child = parent* 2+1;while (child < n){if (child+1 < n && a[child + 1] < a[child]){child++;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent*2 +1;}else{break;}}
}

三、堆排序的实现代码

3.1 如何利用向上调整建堆

向上调整的思想大家都懂了，而建堆的话我们可以这样想：

• 从数据的第一个数每次向上调整这样
• 当调整到最后一个数的时候前面所有的都是已经调整好的堆

📚 代码演示：

//向上调整
void adjustup(HeapTypeData* a, int child)
{int parent = (child - 1) / 2;while (child > 0){//建小堆if (a[child] > a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (parent - 1) / 2;}else{break;}}}
//向上调整建堆  OR 建小堆降序 
//                建大堆升序
for (int i = 1; i < n; i++)
{adjustup(a, i);
}

3.1 如何利用向下调整建堆

利用向下调整建堆的要求是左右俩边都是堆才可以向下调整：

• 那么我们可以把他分为 分治子问题 先向下调整左右子树的在一部部调整堆顶

• 而堆的最后一个子树一定是堆

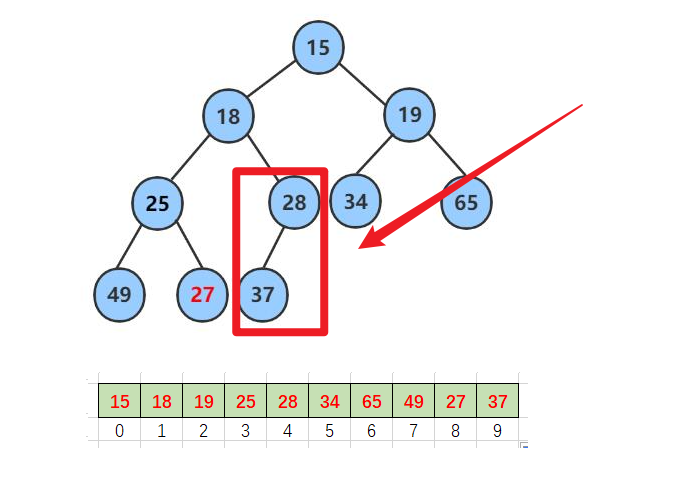
这样我们就可以利用数组存储堆的特性 父节点等于子节点 -1除2

• parent = （child-1）/ 2 ;
• 然后再利用循环 减减 把每个子树都调整完到堆顶堆就减好了

📚 代码演示：

//向下调整
void adjustdown(HeapTypeData* a, int n, int parent)
{int child = parent* 2+1;while (child < n){if (child+1 < n && a[child + 1] > a[child]){child++;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent*2 +1;}else{break;}}
}//向上调整建堆  OR 建小堆降序 
//                建大堆升序
for (int i = (n-1-1)/2; i > 0; i--)
{adjustdown(a, n, i);
}

3.3 堆建完了如何排序数据

堆我们建完了，排序难道一个个把堆顶数据取出然后再放进去吗? 当然不是排序算法都是在数组的 原本空间上进行排序：

• 我们的思想还是和删除 POP 一样先把堆顶的数据和堆底进行交换
• 然后再利用下标减减删除数据，（虚拟删除其实还在）
• 这样每次最大或者最小的数据都被按规律放在原空间里面了

📚 代码演示：

//开始排序int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);adjustdown(a, end, 0);end--;}

3.4 堆排完整代码

//向上调整
void adjustup(HeapTypeData* a, int child)
{int parent = (child - 1) / 2;while (child > 0){//建小堆if (a[child] > a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (parent - 1) / 2;}else{break;}}}
//向下调整
void adjustdown(HeapTypeData* a, int n, int parent)
{int child = parent* 2+1;while (child < n){if (child+1 < n && a[child + 1] > a[child]){child++;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent*2 +1;}else{break;}}
}void HeapSort(int* a, int n)
{//向上调整建堆  OR 建小堆降序 //                建大堆升序/*for (int i = 1; i < n; i++){adjustup(a, i);}*/for (int i = (n-1-1)/2; i > 0; i--){adjustdown(a, n, i);}//开始排序int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);adjustdown(a, end, 0);end--;}
}

四、俩种实现方式的效率对比

4.1 向上调整建堆时间复杂度计算

4.2 向下调整建堆时间复杂度计算

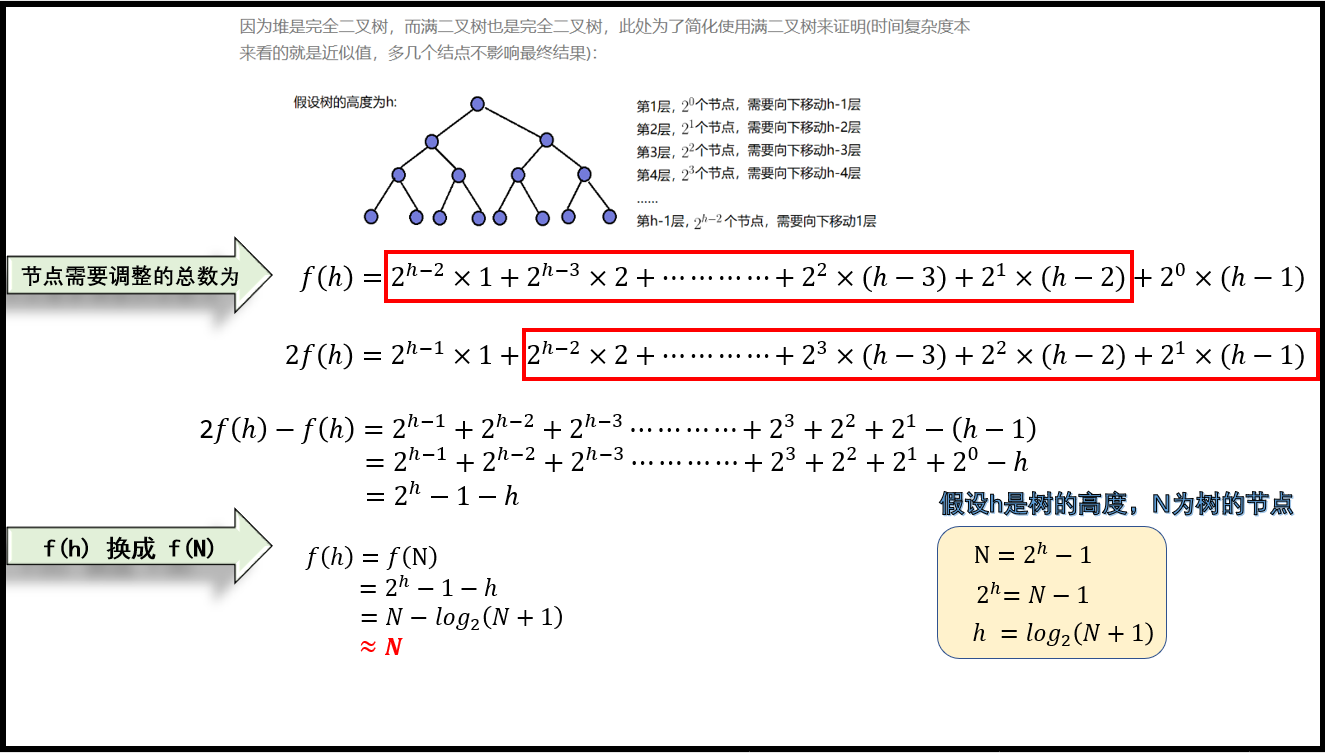
4.3 对比结果

建堆思想	时间复杂度
向上调整建堆	O(N * logN)
向下调整建堆	O(N)

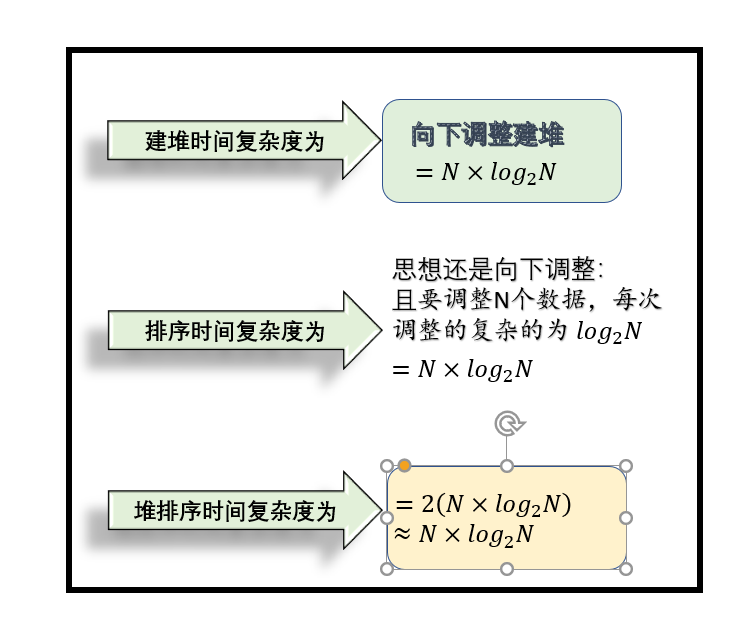
🔥 所以我们在进行堆排序的时候一定首先选取向下调整算法时间复杂度更优。

• 假设有1000万个数据

建堆思想	排序次数
向上调整	1000W*24（约等于 2亿多）
向下调整	1000W

所以我们向下调整的算法是远远大于向上调整的这是为什么呢？

• 🔥 因为 向下调整最后一层节点多且全部需要调整到第一层（调整h-1次）
• 🔥 而向下调整 最后一层不需要调整，越是接近底层调整越少

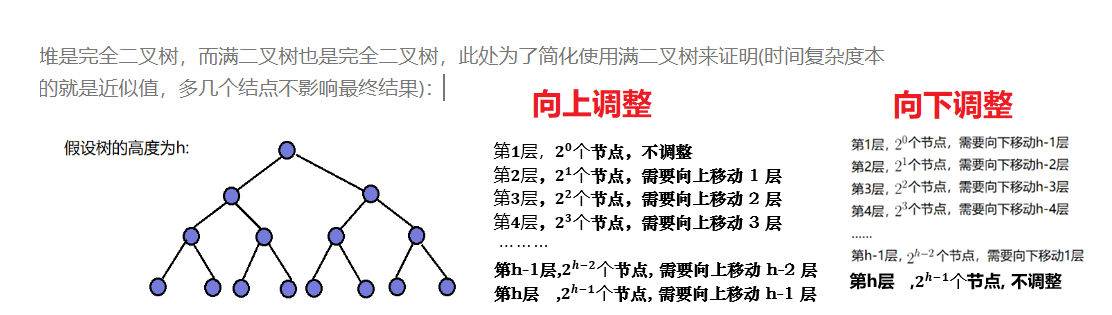
4.4 堆的时间复杂度计算

📝文章结语：

☁️ 以上就是本章的全部内容了，各位铁汁们快去试试吧！
看到这里了还不给博主扣个：
⛳️ 点赞☀️收藏 ⭐️ 关注！
💛 💙 💜 ❤️ 💚💓 💗 💕 💞 💘 💖
拜托拜托这个真的很重要！
你们的点赞就是博主更新最大的动力！
有问题可以评论或者私信呢秒回哦。