论文链接:微电网两阶段鲁棒优化经济调度方法 - 中国知网
代码链接:https://m.tb.cn/h.5Mg7fCo?tk=hnpmWgZiv2R
复现效果:
运行环境:Matlab 2020b+Cplex+yalmip
1 微电网结构
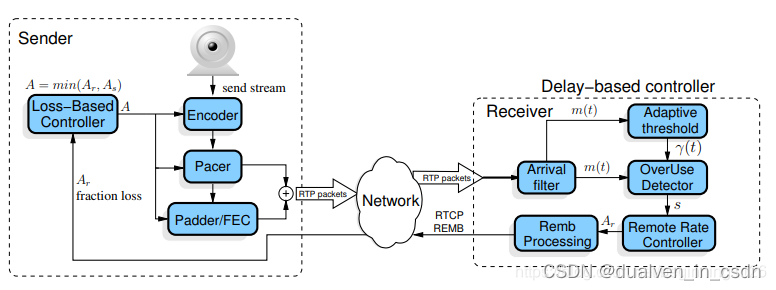
图 1 所示为典型的微电网结构,由可控分布式电源、可再生分布式电源、储能及本地负荷集成而成。 此外, 考虑微电网内包含需求响应负荷的情况,微电网可通过灵活调整需求响应负荷的用电计划,降低运行成本。

图 1 微电网结构
2 系统模型
2.1 微型燃气轮机
微型燃气轮机的成本函数,
![]()
微型燃气轮机的约束条件,由于微型燃气轮机的功率响应速度相对于小时级调度而言较快,
因此不考虑其爬坡率约束,仅考虑输出功率约束:
| 输出功率最大/最小约束: |
2.2 储能
储能的成本函数,
![]()
储能的约束条件,
| 储能的充电功率最大/最小约束: | |
| 储能的放电功率最大/最小约束: | |
| 储能在调度的始末时刻容量相等: |  |
| 储能各时段的剩余容量约束: |  |
2.3 需求响应负荷
需求响应负荷的成本函数,式(10)中的绝对值项用于表示实际调度功率和期望用电功率之间的偏差,通过引入辅助变量及约束可将其化为式(11)所示的线性形式。
![]()
![]()
需求响应负荷的约束条件,
| 需求响应负荷最大/最小约束: | |
| 需求响应功率平衡约束: | |
| 需求响应功率最小约束: |
2.4 配电网交互功率
配电网之间的交互功率的成本函数,
![]()
配电网之间的交互功率的约束条件,
| 功率平衡约束: | 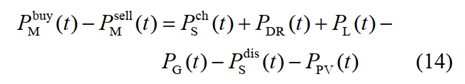 |
| 微电网向配电网购买的功率约束: | |
| 微电网向配电网出售的功率约束: |
3 两阶段鲁棒优化模型
3.1 目标函数
微电网的运行目标为日运行成本最小化,如式(18)所示,包括上述的约束条件。

3.2 确定性优化模型
当不考虑光伏出力和负荷功率的不确定性时,可得到上述微电网经济调度问题的确定性优化模
型,其紧凑形式可表述为:

式中 x、 y 为优化变量,具体表达式为:
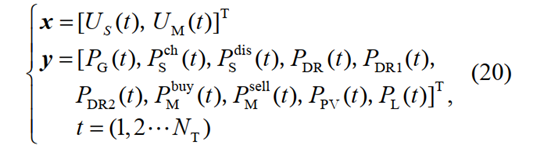
在确定性模型中,光伏出力和负荷功率的为预测值,并没有考虑预测误差的影响。
![]()
| 参数 | 参数说明 |
| 目标函数(18)对应的系数列向量 | |
| 对应约束下变量的系数矩阵 | |
| 常数列向量 | |
| 不等式约束,包括式(2)、(7)、(9)、(13) | |
| 等式约束,等式不一定为0,代码中为Ky=g,包括式(6)、(8)、(12)、(14) | |
| 双向约束,包括式(4)、(5)、(15)、(16) | |
| 确定性优化模型约束,光伏出力和负荷功率的取值为各时段相应的预测值 | |
| 光伏出力、负荷功率的预测值 |
3.3 不确定性优化模型
确定性优化模型得到的方案往往显得过于“冒险”,需要在模型中计及不确定性的影响。考虑光伏出力和负荷功率的波动范围位于式(22)所构建的箱型不确定集 U 内:

文章搭建的两阶段鲁棒优化模型的目的在于找到不确定变量u在不确定集U内朝着最恶劣场景变化时经济性最优的调度方案,具有如下形式:
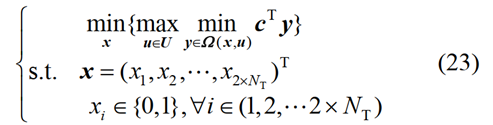
公式理解:外层的最小化为第一阶段问题,优化变量为x;内层的最大最小化为第二阶段问题, 优化变量为 u 和 y,其中的最小化问题等同于式(19)的目标函数,表示最小化运行成本;max 结构的目的就在于找到导致运行成本最大的最恶劣场景。
整体的思路就是给定一组(x,u),但此时的u是不确定的,要考虑光伏和负荷的预测误差,考虑到此时最恶劣的场景也就确定了u,确定了(x,u)后此时的问题也就转变为确定性的场景,最后求解y,使运行成本最小化,得到各个设备的出力结果。
4 求解推导
对偶理论理解:我们在求解最优化问题时,常常不知道什么时候优化结束,也不知道该问题的最优值究竟是多少,求解的最优值可能与真实的最优值差距很大。对偶理论在一定程度上为我们获得的这个解提供一个下界。例如,我们求解一个最优化问题时,发现目标函数值迭代到100附近就迭代不动了。这时,你去求解它的对偶问题,发现对偶问题的最优函数值是95。可以确定原问题的最优值一定大于95,目前已经求解到100,可以停止迭代求解。关于对偶理论的理解可以参考如下的文章和视频:
文章:最优化3: 对偶 - 知乎
视频:最优化理论与方法-第十讲-约束优化(三):对偶理论_哔哩哔哩_bilibili
原问题:

对原问题进行分解,得到的主问题形式为:

进一步将原问题表达为如下形式:

引入各约束的对偶变量:
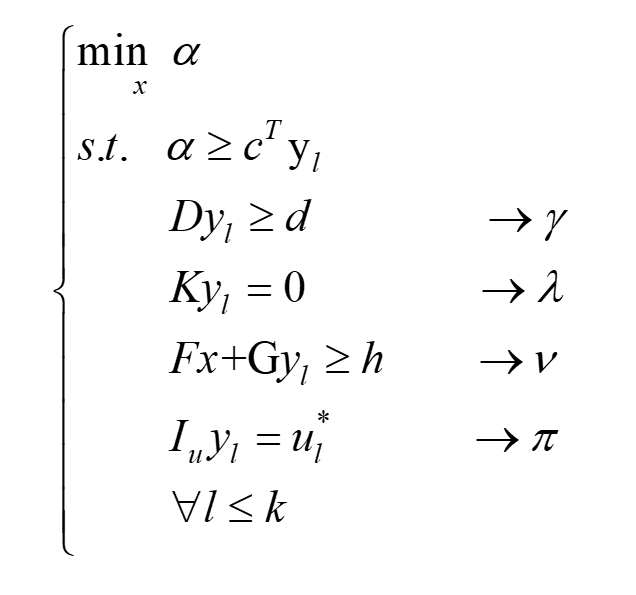
转化为标准形式:

写出Lagrange函数:
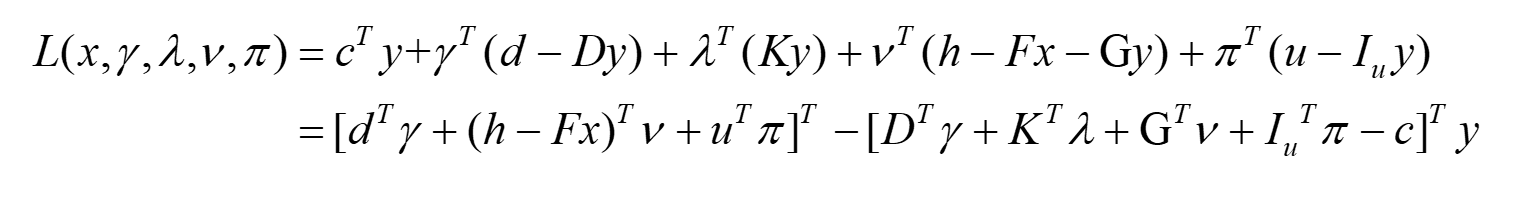
进一步求Lagrange函数的最值:

如果![]() 可行,这里如果为等式约束,对偶变量没有大小限制,作者对该问题做了修正,文章中的
可行,这里如果为等式约束,对偶变量没有大小限制,作者对该问题做了修正,文章中的![]() 可以去除,推出:
可以去除,推出:
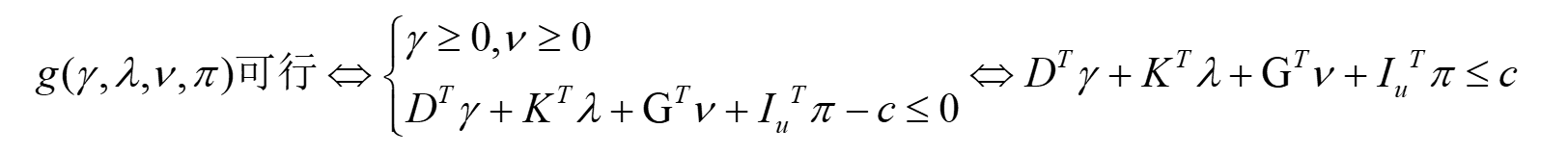
最后将其转化为 max 形式,并与外层的 max 问题合并,最后得到如下对偶问题:

该对偶问题最优解所对应的 u*为不确定集 U 的一个极点,也就是说,式(27)取到最大值时,不确定变量 u 的取值应为上式所描述的波动区间的边界。此外,在本文所研究的微电网中,光伏出力取到区间的最小值和负荷功率取到区间的最大值时,微电网的运行成本更高,更符合“最恶劣”场景的定义,因此可将式(22)改写成如下形式:
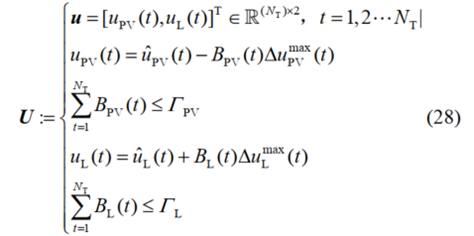
将式(28)中的不确定变量表达式代入式(27)后,将出现二进制变量和连续变量乘积的形式,通过引入辅助变量和相关约束对其进行线性化,最后得到:

5 代码详解
5.1 设置参数
%% 设参
%微型燃气轮机
pm_max=1500; %联络线功率上限
eta=0.95; %储能充放电效率
p_g_max=800; %出力上限
p_g_min=80; %出力下限
a=0.67; %成本系数
b=0; %成本系数
%储能
ps_max=500; %充放电功率上限
ES_max=1800; %荷电状态上限
ES_min=400; %荷电状态下限
ES0=1000; %初始荷电状态
KS=0.38; %单位充放电成本
%需求响应
DDR=2940; %总用电需求
DR_max=200; %最大用电需求
DR_min=50; %最小用电需求
KDR=0.32; %单位调度成本
%分时电价
price = [0.48;0.48;0.48;0.48;0.48;0.48;0.48;0.9;1.35;1.35;1.35;0.9;0.9;0.9;0.9;0.9;0.9;0.9;1.35;1.35;1.35;1.35;1.35;0.48];
%风电、光伏、负荷预测值
PW_=[0.6564 0.6399 0.6079 0.5594 0.5869 0.5794 0.6138 0.6192 0.6811 0.6400 0.7855 0.7615 0.6861 0.8780 0.6715 0.7023 0.6464 0.6321 0.6819 0.6943 0.7405 0.6727 0.6822 0.6878];
p_pv=1500*[ 0 0 0 0 0 0.0465 0.1466 0.3135 0.4756 0.5213 0.6563 1.0000 0.7422 0.6817 0.4972 0.4629 0.2808 0.0948 0.0109 0 0 0 0 0];
PL=1500*[ 0.4658 0.4601 0.5574 0.5325 0.5744 0.6061 0.6106 0.6636 0.7410 0.7080 0.7598 0.8766 0.7646 0.7511 0.6721 0.5869 0.6159 0.6378 0.6142 0.6752 0.6397 0.5974 0.5432 0.4803];
%需求响应负荷的期望用电功率
P_DR=1*[110 100 90 80 100 100 130 100 120 160 175 200 140 100 100 120 140 150 190 200 200 190 80 60];决策变量也就是待求的变量
%% 设决策变量
%储能
p_ch=sdpvar(1,24,'full'); %储能充电
p_dis=sdpvar(1,24,'full'); %储能放电
us=binvar(1,24,'full'); %充放电标识
%配电网
p_buy=sdpvar(1,24,'full'); %配网购电
p_sell=sdpvar(1,24,'full'); %配网售电
um=binvar(1,24,'full'); %购售电标识
%分布式电源
%p_pv=sdpvar(1,24,'full'); %光伏发电
%pL=sdpvar(1,24,'full'); %固定日负荷
p_g=sdpvar(1,24,'full'); %分布式电源
%负荷
PDR=sdpvar(1,24,'full'); %可转移负荷
PDR1=sdpvar(1,24,'full'); %可转移负荷辅助变量
PDR2=sdpvar(1,24,'full'); %可转移负荷辅助变量
afa=sdpvar(1,1,'full');5.2 约束条件
%% 约束条件
%分布式电源约束
C=[-Q1*y>=-p_g_max]; %分布式电源的功率小于最大功率
C=C+[Q1*y>=p_g_min]; %分布式电源的功率大于最小功率%储能约束
C=C+[-Q31*y-ps_max*Q01*x>=-ps_max]; %储能充电功率不能超过最大充电功率
C=C+[-Q32*y>=-Q01*x*ps_max]; %储能放电功率不能超过最大放电功率
C=C+[Q31*y>=0]; %储能充电功率必须非负
C=C+[Q32*y>=0]; %储能放电功率必须非负
C=C+[Q2*y==0]; %保证储能在调度前后能量相同
C=C+[-Q4*y>=-(ES_max-ES0)]; %储能量不能超过最大储能量
C=C+[Q4*y>=(ES_min-ES0)]; %储能量不能低于最小储能量%配电网交互约束
C=C+[-Q52*y-pm_max*Q02*x>=-pm_max]; %出售电力的功率减去电力市场交易的功率不小于最大功率
C=C+[-Q51*y>=-Q02*x*pm_max]; %出售电力的功率不小于电力市场交易的功率乘以最大功率
C=C+[Q51*y>=0]; %出售电力的功率大于等于零
C=C+[Q52*y>=0]; %购买电力的功率大于等于零
C=C+[Q6*y+G1*u==0]; %功率平衡的约束条件%可转移负荷约束
C=C+[Q8*y==DDR]; %表示可转移负荷的功率需求的上下限约束,确保可转移负荷的功率在一定范围内
C=C+[-Q9*y>=-DR_max]; %可转移负荷的功率小于最大用电需求
C=C+[Q9*y>=DR_min]; %可转移负荷的功率大于最小用电需求
C=C+[Q101*y>=0]; %大于等于零
C=C+[Q102*y>=0]; %大于等于零
%C=C+[Q9*y+Q101*y-Q102*y=P_DR];
C=C+[Q103*y==P_DR'];
5.3 目标函数
求解问题可以表述为如下的紧凑形式,然后构建紧凑形式的系数矩阵,进一步通过矩阵来表达求解的问题。
%% 紧凑形式
%cy
%Dy>=d
%Ky=g
%Fx+Gy>=h
%Ly+Yu=0%紧凑后的目标函数
c=QC;
%紧凑后的约束条件
C=C+[D*y>=d];
C=C+[K*y==g];
C=C+[F*x+G*y>=h];
C=C+[L*y+Y*u==0];
C=C+[afa>=c*y];%系数矩阵定义
x=[us,um]'; %第一阶段变量,使用转置操作将其转换为列向量
y=[p_g,p_ch,p_dis,PDR,PDR1,PDR2,p_buy,p_sell]'; %第二阶段变量,同样使用转置操作D=[-Q1;Q1;Q31;Q32;-Q4;Q4;Q51;Q52;-Q9;Q9;Q101;Q102];
d=[-p_g_max*ones(24,1);p_g_min*ones(24,1);0*ones(24,1);0*ones(24,1);-(ES_max-ES0)*ones(24,1);(ES_min-ES0)*ones(24,1);0*ones(24,1);0*ones(24,1);-DR_max*ones(24,1);DR_min*ones(24,1);0*ones(24,1);0*ones(24,1)];K=[Q2;Q8;Q103];
g=[0;DDR;P_DR'.*ones(24,1)];F=[-ps_max*Q01;ps_max*Q01;-pm_max*Q02;pm_max*Q02];
G=[-Q31;-Q32;-Q52;-Q51];
h=[-ps_max*ones(24,1);0*ones(24,1);-pm_max*ones(24,1);0*ones(24,1)];L=[Q6];
Y=[G1];
决策变量x是一个48维的列向量:
x=[US,UM]T
决策变量y是一个240维的列向量:
y=[PG,PSch,PSdis,PDR,PDR1,PDR2,PMbuy,PMsell,PPV,PL]T
D是一个144行240列的矩阵,d是一个144维的列向量,E24表示24阶的单位矩阵,L24表示下三角和对角线全为1的矩阵,上三角全为0的矩阵。Dy≥d写成矩阵形式:

K是一个50行240列的矩阵,k是一个50维的列向量,Ky=g写成矩阵形式:
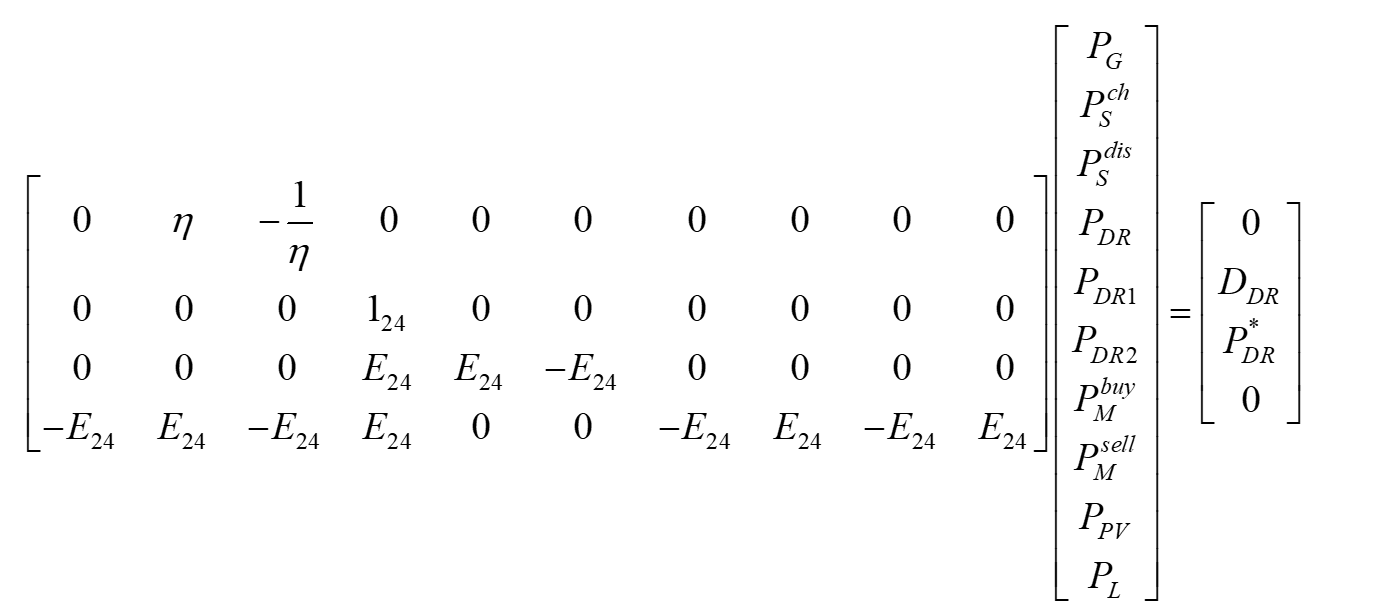
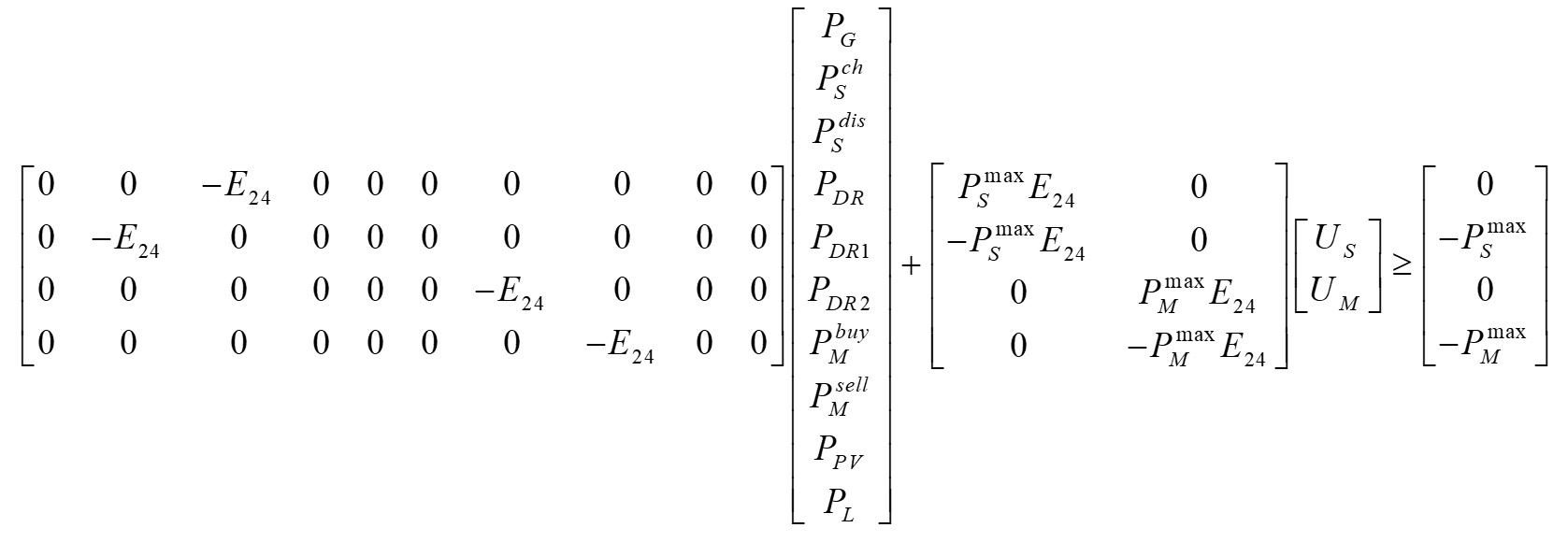
F是一个96行48列的矩阵,G是一个96行240列的矩阵,h为96维的列向量,Fx+Gy≥h写成矩阵形式:
![]() 是一个48行240列的矩阵,
是一个48行240列的矩阵,![]() 是48维的列向量,
是48维的列向量,![]() 写成矩阵形式:
写成矩阵形式:

5.4 问题求解
%% 迭代求解两阶段鲁棒优化问题
% 先运行一次
[x,LB,y] = MP2(); %调用函数MP2
[u,UB] = SP(x); %调用函数SP(),传入MP2()中返回的参数x
UB1 = UB; %将函数SP()的返回值UB的值赋给UB1
p(1)= UB1 - LB; %计算UB1-LB,并将结果赋给数组p的第一个元素。
%开始迭代
for k=1:4[x,LB,y] = MP(u); %调用函数MP()[u,UB] = SP(x); %调用函数SP(),传入MP2()中返回的参数xUB = min(UB1,UB); %取UB1和UB中较小的值p(k+1) = UB-LB; %计算UB-LB,并将结果赋给数组p的其他元素
end
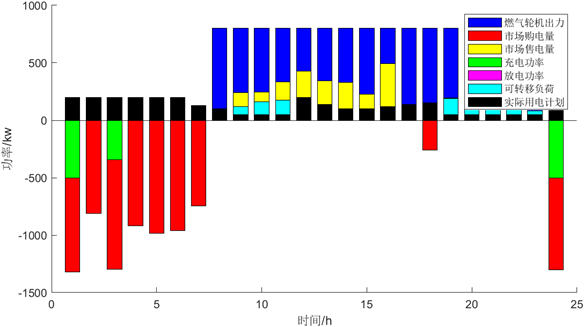
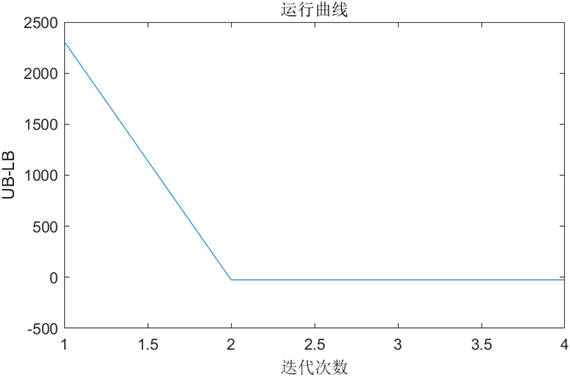
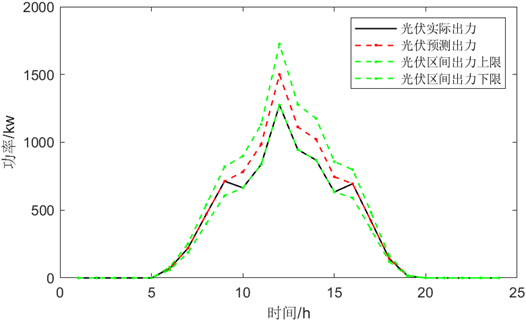
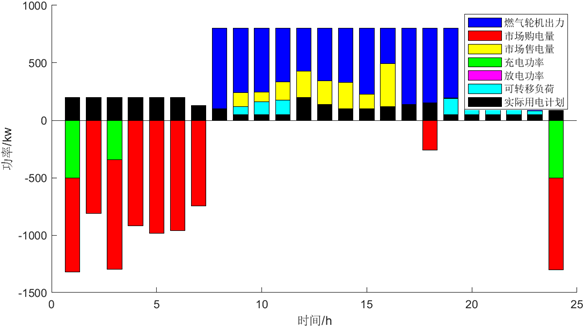
5.5 运行可视化