动态规划

动态规划就像是解决问题的一种策略，它可以帮助我们更高效地找到问题的解决方案。这个策略的核心思想就是将问题分解为一系列的小问题，并将每个小问题的解保存起来。这样，当我们需要解决原始问题的时候，我们就可以直接利用已经计算好的小问题的解，而不需要重复计算。

动态规划与数学归纳法思想上十分相似。

数学归纳法：

1. 基础步骤（base case）：首先证明命题在最小的基础情况下成立。通常这是一个较简单的情况，可以直接验证命题是否成立。

2. 归纳步骤（inductive step）：假设命题在某个情况下成立，然后证明在下一个情况下也成立。这个证明可以通过推理推断出结论或使用一些已知的规律来得到。

通过反复迭代归纳步骤，我们可以推导出命题在所有情况下成立的结论。

动态规划：

1. 状态表示：

2. 状态转移方程：

3. 初始化：

4. 填表顺序：

5. 返回值：

数学归纳法的基础步骤相当于动态规划中初始化步骤。

数学归纳法的归纳步骤相当于动态规划中推导状态转移方程。

动态规划的思想和数学归纳法思想类似。

在动态规划中，首先得到状态在最小的基础情况下的值，然后通过状态转移方程，得到下一个状态的值，反复迭代，最终得到我们期望的状态下的值。

接下来我们通过三道例题，深入理解动态规划思想，以及实现动态规划的具体步骤。

---

91. 解码方法

题目解析

我们先把动态规划五个步骤抄过来。

1. 状态表示：

2. 状态转移方程：

3. 初始化：

4. 填表顺序：

5. 返回值：

状态表示

动态规划思想和数学归纳法相似，由一个简单情况下的解，通过状态转移方程，推导出其他的状态，最后返回我们希望得到的状态。

状态表示通常由经验加题目得到。

经验是指，以某个位置为结尾，或者以某个位置为开头。

题目给我们一个字符串，需要我们返回解码方法的总和。

我们可以定义，dp[i]表示从0下标字符开始，一直到i下标字符结尾，这段字符串的解码方法数。

状态转移方程

我们想一想dp[i]能不能由其他的状态推导得出来，dp[i]与其他状态的联系是什么？

我们可以单独考虑i下标字符的状态，在0下标字符一直到i下标字符，这段字符串我们称为s，s字符串中，i下标字符的状态是什么？

i下标字符肯定是0-9其中之一，如果我们要对s字符串进行解码，i字符要么单独解码，要么和i-1下标字符结合一起解码，对于i下标字符一共就这两种情况。

如果是单独解码情况，i一定是1-9其中之一，0不能单独解码。

如果是与i-1下标字符结合解码，那么i-1与i组合一定是10-26的数字，对于i-1数组不能是0，只能是1或者2。

根据这两种情况我们就可以得到状态转移方程，

如果s[i]!='0'，那么我们就考虑单独解码情况，如果单独解码，他的解码数就是dp[i-1]。

dp [i-1]是0-（i-1）之间的解码总数，对于这些解码的每一条情况，我们都可以在末尾添加对i单独解码的步骤，所以i单独解码情况下的解码数就是dp[i-1]。

如果10<=(s[i-1]-'0')*10+s[i]-'0'<=26，那我们就考虑与i-1结合解码情况，他的解码数就是dp[i-2]。

dp[i-2]是0-(i-2)之间的解码总数，对于这些解码的每一条情况，我们都可以在末尾添加i-1与i结合解码的情况，所以结合解码情况下的解码数就是dp[i-2]

我们要求的是i的解码总数，所以需要把这两种情况的解码数加上。

状态转移方程，即：

if(s[i]!='0') dp[i]+=dp[i-1]；

if(10<=(s[i-1]-'0')*10+s[i]-'0'<=26) dp[i]+=dp[i-2]；

初始化

初始化就是确定最小的基础解，然后由状态转移方程，以最基础的解推导出其他的解，最后返回我们希望得到的解。

由状态转移方程，我们求dp[i]需要dp[i-1]和dp[i-2]的值，所以我们需要初始化前两个数据。

在这道题中，我们发现初始化前两个数据的值，这个过程的实现其实也挺复杂的，我们希望有更加简便的初始化方式。

对于这种情况，我们通常可以在dp数组中添加虚拟节点。

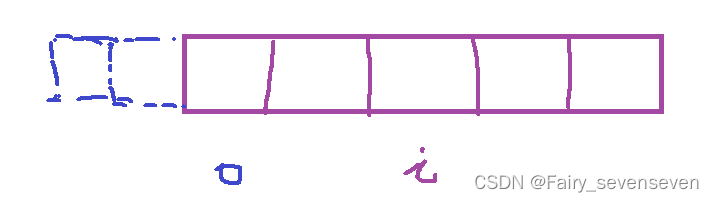
在原先下标0前面添加两个虚拟结点，这样我们就可以正常从0开始遍历，也不会产生越界的情况。

如果要实现，就需要把原数据全部往后移2个位置，也就是我们的dp状态表示需要修正一下，定义dp[i]对应s数组[i-2]位置的元素，从第一个元素开始到s数组中i-1下标元素，这段字符串中的解码总数。

需要注意的两个点，1.虚拟结点里面的值，不能影响其他值的正常求解。

2.注意dp数组与s数组的对应关系。

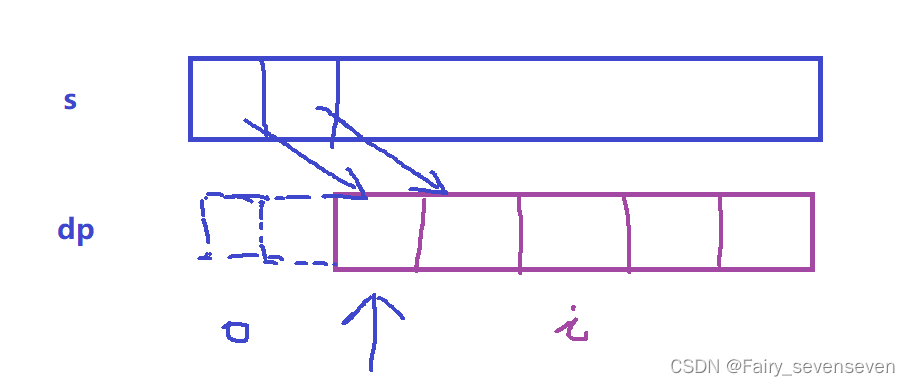
if(s[i-2]!='0') dp[i]+=dp[i-1]；

if(10<=(s[i-3]-'0')*10+s[i-2]-'0'<=26) dp[i]+=dp[i-2]；

注意这段代码的改动。dp表下标与s表下标的对应关系。

如果我们要填第一个值，同样考虑两种情况，单独解码或者与前面数结合解码。

单独解码，如果不为0，单独解码情况解码数是1，所以1下标初始化为1.

结合解码，不存在，结合解码解码数是0，所以0下标初始化为0。

对应状态转移方程，不能有影响。

所以初始化，即：

dp[0]=0,dp[1]=1;

填表顺序

从左往右

返回值

dp[n],返回最后一个元素即可。

代码实现

int numDecodings(char* s) {int n=strlen(s);int dp[n+2];memset(dp,0,sizeof(dp));dp[0]=0;dp[1]=1;for(int i=2;i<n+2;i++){if(s[i-2]!='0') dp[i]+=dp[i-1];if(i-3>=0){int t=(s[i-3]-'0')*10+(s[i-2]-'0');if(t>=10&&t<=26) dp[i]+=dp[i-2];}else{dp[i]+=dp[i-2];}}return dp[n+1];
}

首先用n变量接收s数组的数组大小。

多创建两个空间大小，前两个空间是虚拟节点，作用是统一每一个状态的填写、遍历。

初始化前两个虚拟节点的数据。

从i=2开始遍历，一直到最后一个位置。

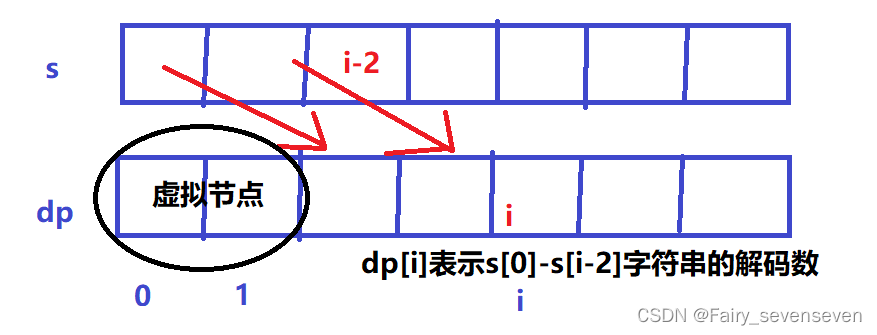
dp[i]表示s[0]--s[i-2]字符串的编码数。

---

62. 不同路径

题目解析

机器人每次只能往右边走一步，或者往下边走一步，最后到达网格的右下角，求一共有多少条不同的路径。

状态表示

我们可以创建这样的dp表，dp[i][j]表示从第1行，第1列出发，到达第i行，第j列时的不同路径数。

状态转移方程

我们想一想dp[i][j]的状态能不能由其他的状态推导得出。

针对于dp[i][j]如果我们要走到i,j位置，要么从（i-1，j）往下走一步，要么从（i，j-1）往右走一步，这两种情况。

对于第一种情况，dp[i-1][j]表示从（1,1）出发，到达（i-1，j）的路径数，对于每一条路径最后都添加一步，往下走一步，到达（i，j），这样的路径就是从（1，1）出发到达（i，j）的路径，这样的路径有多少条呢？一共就是dp[i-1][j]条。

对于第二种情况，同理，一共有dp[i][j-1] 条。

所以dp[i][j]=dp[i-1][j]+dp[i][j-1]。

回想一下数学归纳法，我们知道最小的基础解，知道每一相邻状态的推导，是否可以从最小的基础的状态依次推导出我们希望得到的状态？答案是肯定的。

初始化

我们需要把dp表中第一行到第三行，第一列到第七列中所有的空都填上。

我们可以从（1,1）位置开始遍历，这样我们就做到了统一，统一的意思是dp表中所有有意义的状态，都可以通过状态转移方程推导得到，这样推导出（1,1）位置我们就需要初始化前驱。

由状态转移方程知，dp[i][j]=dp[i-1][j]+dp[i][j-1]

我们需要使得dp[0][1]+dp[1][0]的值是1，可以把数组全部置0，然后选一个（0,1）（1，0）选一个位置置1就可以了。

这样我们就可以通过状态转移方程推导出（1,1）

接着我们看（1，1）能不能一直推导下去。

推导（i，j）需要(i,j-1)（i-1，j）位置的状态。

如果我们要得到第一行的值，需要第零行的状态，而我们初始化为0，是否会影响推导的结果？想一想状态转移方程的意义，要么从上面往下走一步，要么从左边往右走一步，上面没有路可以走，就表示没有这个路径，所以上面的路径数是0，不会影响结果。那么推导第一行是不会出问题的。

同理推导第一列的时候，我们需要第零列的状态值，同理，置0是没有问题的。

这样我们就可以通过已经初始化的值，推导出所有状态。

所以初始化为：

全部置0，然后

dp[0][1]=1 dp[1][0]=0

或者

全部置0，然后

dp[1][0]=1,dp[0][1]=0

填表顺序

从左往右，从上往下

返回值

返回dp[m][n]，dp[i][j]表示从第1行，第1列出发，到达第i行，第j列时的不同路径数。

代码实现

int uniquePaths(int m, int n) {int dp[m+1][n+1];for(int i=0;i<=m;i++){memset(dp[i],0,sizeof(dp[i]));}dp[0][1]=1;for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){dp[i][j]=dp[i-1][j]+dp[i][j-1];}}return dp[m][n];}

代码实现的步骤：

1. 创建dp表

2. 初始化

3. 填表

4. 返回值

---

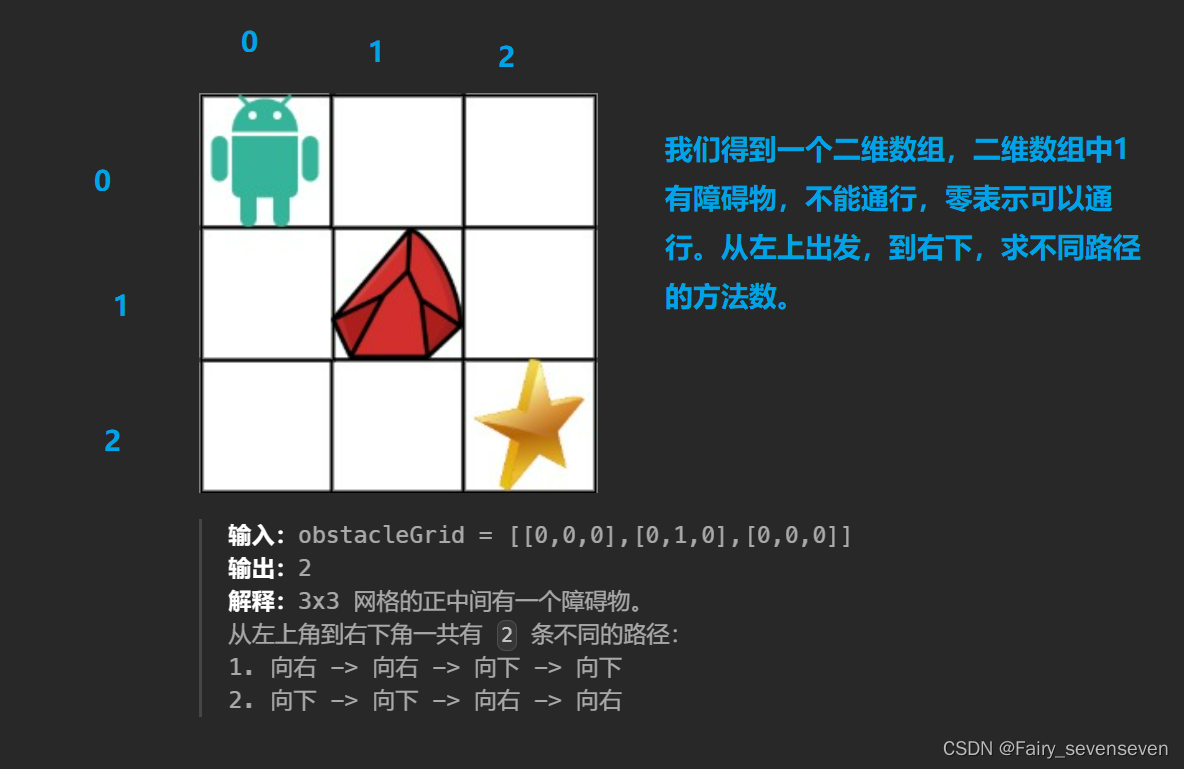
63. 不同路径 II

题目解析

状态表示

我们可以统一遍历每一个dp状态，创建虚拟节点，也可以直接初始化，不创建虚拟节点，上一道题目我们创建了虚拟节点，对状态推导进行统一化，这道题我们就不创建虚拟节点，直接初始化。

此时我们可以定义dp[i][j]表示从（0,0）开始到达（i，j）位置不同路径的方法数。

状态转移方程

对于dp[i][j]位置的状态，首先（i，j）位置要么没有障碍物，要么有障碍物。

如果没有障碍物，那我们就要考虑（i，j）的状态值，想一想其他状态然后推导出该状态，要么从上面往下走一步到（i，j）要么从左边往右走一步到（i，j），所以dp[i][j]=dp[i][j-1]+dp[i-1][j]

如果有障碍物，说明我们没办法到达这个位置，所以到达这个位置的方法数就是0，我们置0即可。

所以状态转移方程为：

if（ob[i][j]==0）dp[i][j]=dp[i][j-1]+dp[i-1][j]

if（ob[i][j]==1) dp[i][j]=0

初始化

由状态状态转移方程我们知道，需要求（i，j）位置的状态，我们需要（i，j-1）和（i-1，j）位置的状态，所以我们需要初始化第一行和第一列的元素。

对于第一行和第一列，如果我们可以到达，方法数一定是1，很容易可以得出，如果我们遇到一个位置不能到达，那么他后面的位置也不能到达。

所以我们把所有位置初始化为0，能到达的位置值1即可。

故初始化：

    for(int i=0;i<row;i++){memset(dp[i],0,sizeof(dp[i]));}for(int j=0;j<col;j++){if(ob[0][j]==1){break;}dp[0][j]=1;}for(int i=0;i<row;i++){if(ob[i][0]==1){break;}dp[i][0]=1;}

填表顺序

从左往右，从上往下

返回值

返回最后一个元素的位置，即dp[row-1][col-1]

代码实现

int uniquePathsWithObstacles(int** ob, int obstacleGridSize, int* obstacleGridColSize) {int row=obstacleGridSize;int col=obstacleGridColSize[0];int dp[row][col];for(int i=0;i<row;i++){memset(dp[i],0,sizeof(dp[i]));}for(int j=0;j<col;j++){if(ob[0][j]==1){break;}dp[0][j]=1;}for(int i=0;i<row;i++){if(ob[i][0]==1){break;}dp[i][0]=1;}for(int i=1;i<row;i++){for(int j=1;j<col;j++){if(ob[i][j]==0){dp[i][j]=dp[i-1][j]+dp[i][j-1];}}}return dp[row-1][col-1];
}

int col=obstacleGridColSize[0];

这条代码可以得到列数。

int dp[row][col];for(int i=0;i<row;i++){memset(dp[i],0,sizeof(dp[i]));}for(int j=0;j<col;j++){if(ob[0][j]==1){break;}dp[0][j]=1;}for(int i=0;i<row;i++){if(ob[i][0]==1){break;}dp[i][0]=1;}

初始化操作，dp表与ob数组一一对应。

    return dp[row-1][col-1];

返回值。

---

结尾

今天我们学习了动态规划的思想，动态规划思想和数学归纳法思想有一些类似，动态规划在模拟数学归纳法的过程，已知一个最简单的基础解，通过得到前项与后项的推导关系，由这个最简单的基础解，我们可以一步一步推导出我们希望得到的那个解，把我们得到的解依次存放在dp数组中，dp数组中对应的状态，就像是数列里面的每一项。最后感谢您阅读我的文章，对于动态规划系列，我会一直更新，如果您觉得内容有帮助，可以点赞加关注，以快速阅读最新文章。

最后，感谢您阅读我的文章，希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点，请随时在评论区留言。

同时，不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中，我将继续探讨这个话题的不同方面，为您呈现更多深度和见解。

谢谢您的支持，期待与您在下一篇文章中再次相遇！