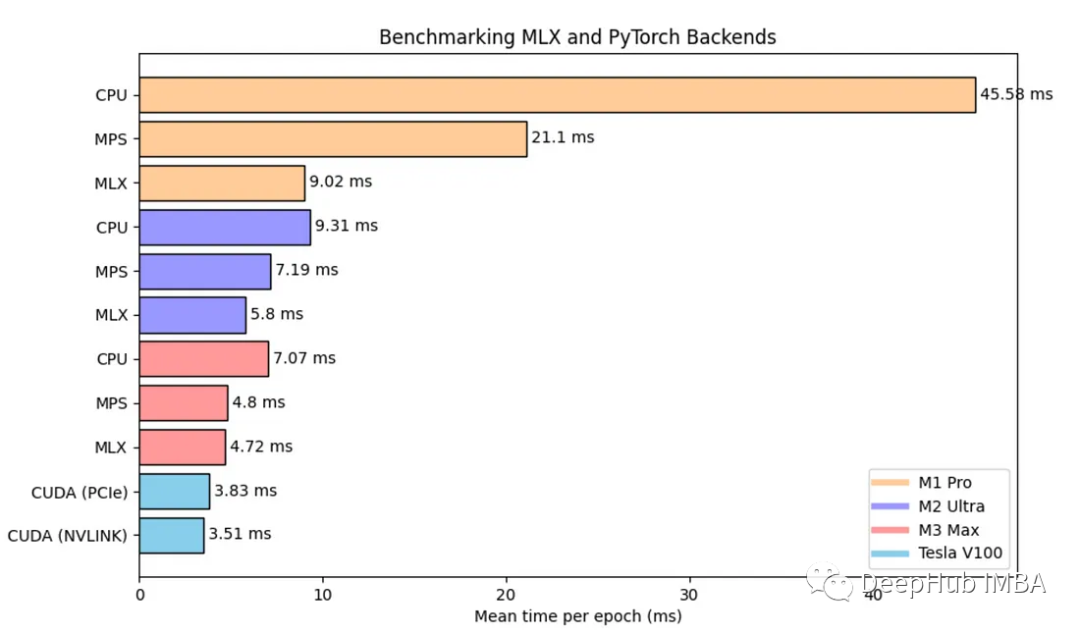
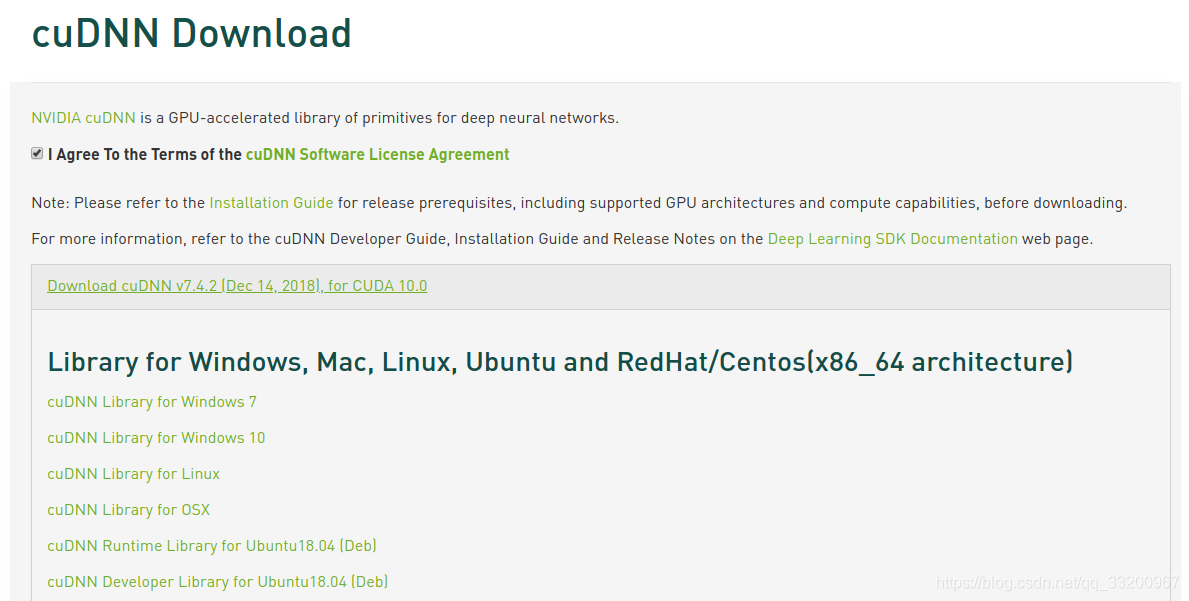
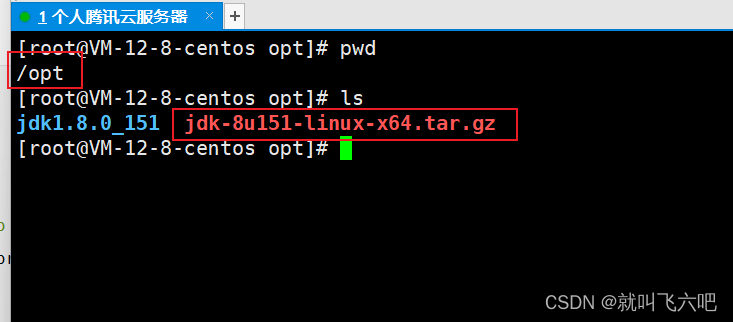
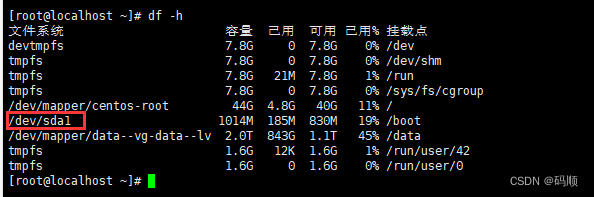
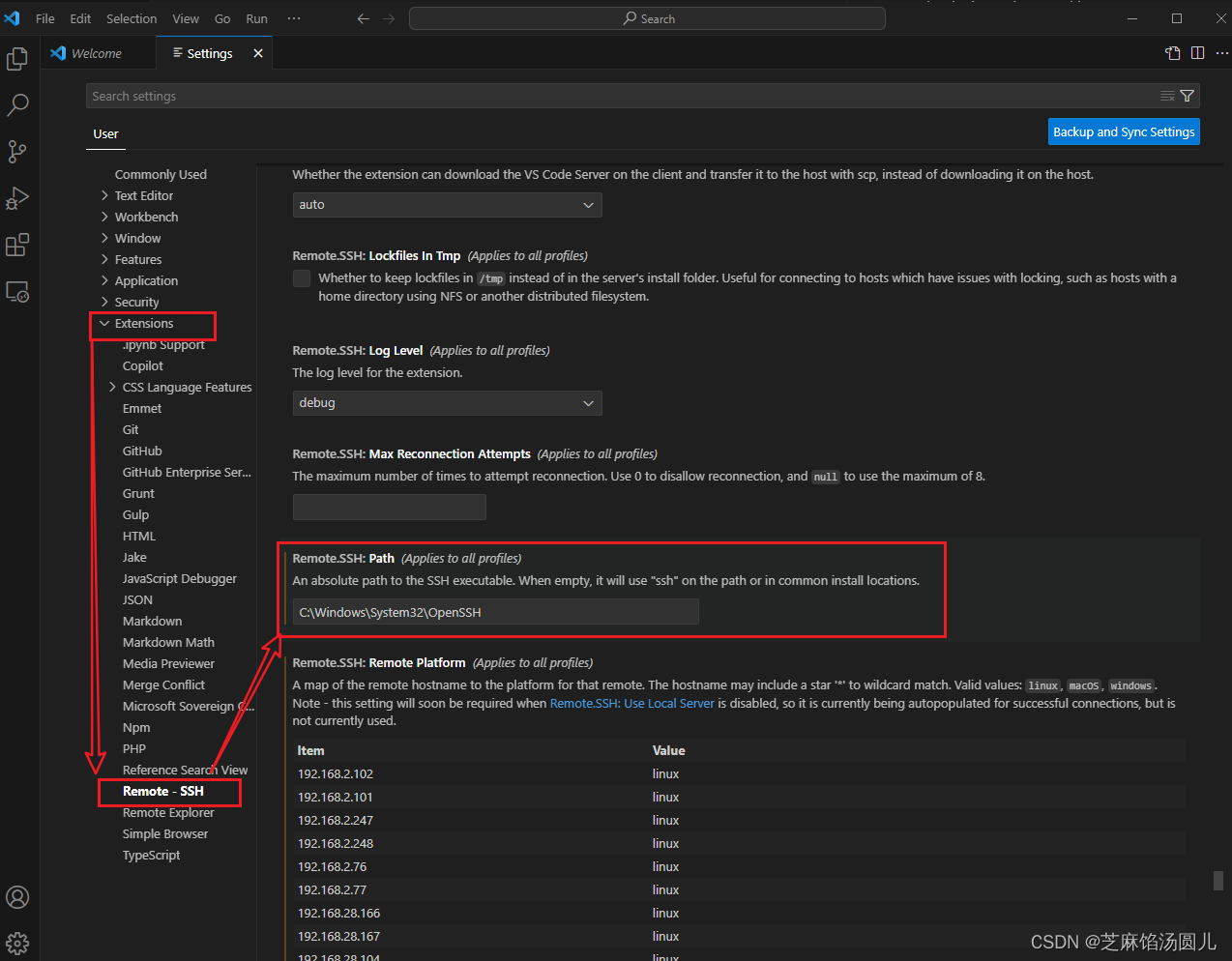
等腰三角形定义: 是指至少有两边相等的三角形。相等的两个边称为这个三角形的腰

二.证明

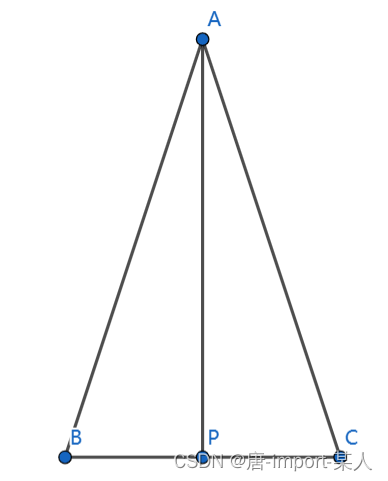
有等腰△ABC,AB和AC是腰,p是BC的中点
证明等腰三角形两底角相等 即$\angle ABP=\angle PCA$
$\therefore$ 三角形内角和为180
$\because \{\begin{array}{l}\angle ABP+\angle APB+\angle BAP=180°\\ \angle ACP+\angle APC+\angle CAP=180°\\ \angle ABC+\angle ACB+\angle BAC=180°\end{array}$

$\therefore AB=AC,p为BC中点$
$\because \angle BAP=\angle CAP=\angle ①,\angle BAC=2\angle ①,AP\perp BC$
$\because \{\begin{array}{l}\angle ABP+\angle APB+\angle ①=180°\\ \angle ACP+\angle APC+\angle ①=180°\\ \angle ABC+\angle ACB+2\angle ①=180°\end{array}$

$\therefore AP\perp BC$
$\because \angle APC=\angle APB=90°$
$\because \{\begin{array}{l}\angle ABP+\angle ①+90°=180°\\ \angle PCA+\angle ①+90°=180°\end{array}$
$\because \angle ABP=\angle PCA$