向量投影：如何将一个向量投影到矩阵的行向量生成子空间？

前言

本问题是在学习Rosen梯度投影优化方法的时候遇到的问题，主要是对于正交投影矩阵(N^T(NN^T)^-1N)的不理解，因此经过查阅资料，学习了关于向量投影的知识，记录如下。

首先需要了解 子空间和子空间的正交补。相关知识可以查阅本人的另外一篇笔记，核和值域的关系：什么是矩阵的秩？，这篇笔记中是以矩阵列向量的生成子空间为例展开的。

核心公式：

1. R ( A H ) ∩ N ( A ) = { 0 } R(A^H) \cap N(A)=\{0\} R(AH)∩N(A)={0}
2. $R(A^H)\oplus N(A)=C^m$

其中R(A^H)是A的行向量的生成子空间， R ( A H ) = { y ∈ R n ∣ y = A H x , x ∈ C m } R(A^H)=\{y\in R^n|y=A^Hx,x\in C^m\} R(AH)={y∈Rn∣y=AHx,x∈Cm}。

N(A)是A的核子空间， N ( A ) = { x ∣ A x = 0 , x ∈ R n } N(A)=\{x|Ax=0,x\in R^n\} N(A)={x∣Ax=0,x∈Rn}。

正文

所谓向量投影，本质上是期望将Rⁿ空间中的任意一个n维向量，分解称为y1+y2，其中y1属于R(A^H)，y2属于N(A)。

1、投影矩阵

投影是一种线性变换，要求两次投影变换的结果等于一次投影变换的结果。在信号处理领域当中，一个信号经过两次滤波器和经过一次滤波器的结果是相等的，那么这个滤波器在数学上可抽象成一个投影矩阵。

写成数学公式：$P^{2}x=PPx=Px$。因此要求投影矩阵P是一个方阵。

可证明：R§=R(P^H)。通常情况下一个方阵的行空间和列空间是不相同的，二者仅仅是同构关系，即维数相同。

即：$R(P)\oplus N(P)=C^n$

投影分为正交投影和斜投影。二者的区别在于，正交投影矩阵P，R§的正交补=N§，等价于，R§和N§正交。而斜投影矩阵则没有这个性质。

可证明：一个投影矩阵P，是正交投影矩阵的充要条件是：P=P^H

举一个简单的例子。

R²空间，向x轴的正交投影P，只能是取一个二维向量的横坐标。R§就是x轴，N§就是y轴，x轴的正交补是y轴。

R²空间，向x轴的斜投影Q，比如是指向东偏南45度➘方向的的投影。R(Q)就是x轴，x轴的正交补是y轴，而N(Q)是沿着东偏南45度➘方向的一维子空间，即N(Q)={ x|x = a(1,-1)^T, a \in R}。

2、如何将一个向量投影到行满秩矩阵A的行向量生成子空间？

现在已知一个行满秩矩阵$A_m^{m\times n}$，R(A^H)是由A的行向量生成的子空间。由上面的例子，可以猜到，n维欧氏空间向R(A^H)的正交投影是唯一的，斜投影是不唯一的（此处考虑典型情况，而非考虑A行列满秩的极端情况）。

现在推导一个由A构成的正交投影矩阵P。

1. $y=y_1+y_2,y_1\in R(A^H),y_2\in R^{\perp }(A^H)$
2. $Py=P(y_1+y_2)=y_1$
3. $y_1\in R(A^H),\therefore y_1=A^{H}x$，x是一个m维的列向量，即y1可表示为A的行向量的线性组合
4. $y_2\in R^{\perp }(A^H)=N(A),A{y}_2=0,Ay=A{A}^{H}x$
5. $x=(A{A}^H{)}^{-1}Ay,y_1=[A^H(A{A}^H{)}^{-1}A]y$
6. $P=A^H(A{A}^H{)}^{-1}A=P^H$

从第5步可以知道为什么需要A行满秩了，只有行满秩的矩阵，$y_1\in R(A^H),y_1=A^{H}x$，其中x才有唯一解。

至此，我们知道$P=A^H(A{A}^H{)}^{-1}A$是一个正交投影矩阵，将一个向量投影到A的行向量的生成子空间。

3、关于Rosen梯度投影法

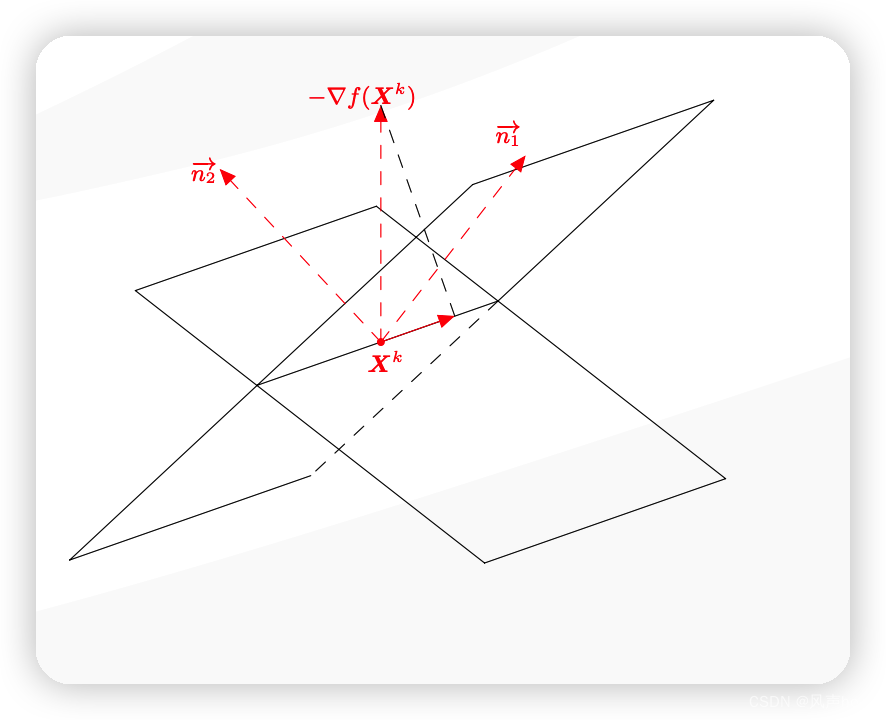
Rosen梯度投影法的可行下降方向：$P^k=Q(-g^k)=(I-N^T(N{N}^T{)}^{-1}N)g^k$

Q是一个投影矩阵，并且投向$N^T(N{N}^T{)}^{-1}N$的正交补空间，N是由积极约束的法向量组成的矩阵，因此P是负梯度方向向积极约束的法向量张成的行空间的正交补的投影。从几何上看，就是将负梯度方向投影向了积极约束的超平面的交线上。

需要注意，Rosen梯度投影法的约束条件是一个多面集。