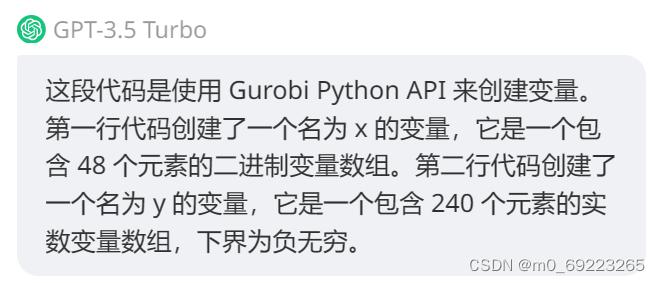
# 建立矩阵模型
m = Model('specification')
x = m.addMVar((48,),vtype=GRB.BINARY,name='x')
y = m.addMVar((240,),lb=-GRB.INFINITY,name='y')
u = m.addMVar((48,),vtype=GRB.BINARY,name='u')

以下是一个简单的示例代码，演示了如何使用 Python 和 Gurobi 库来实现 KKT 方法求解列约束生成算法：

import gurobipy as gp
from gurobipy import GRB# 创建模型
model = gp.Model('column_generation')# 添加变量
x = model.addMVar(name="x", lb=0.0, ub=GRB.INFINITY, shape=10)# 添加目标函数
model.setObjective(x.sum(), GRB.MAXIMIZE)# 添加初始列约束
model.addConstr(x[0] + x[1] <= 1)# 列生成算法迭代
for i in range(10):# 求解子问题submodel = gp.Model('subproblem')y = submodel.addMVar(name="y", lb=0.0, ub=GRB.INFINITY, shape=1)submodel.setObjective(y, GRB.MAXIMIZE)submodel.addConstr(x @ y <= i)  # 添加列约束submodel.optimize()# 获取最优解dual_solution = submodel.getAttr('Pi', submodel.getConstrs())# 检查KKT条件if dual_solution[0] <= 1:break  # KKT条件满足，停止迭代# 添加新的列约束model.addConstr(x @ dual_solution <= 0)# 求解最终问题
model.optimize()# 输出结果
print('最优解:', x.X)

 请注意，这只是一个简单的示例代码，实际的问题可能更加复杂。在实际应用中，您可能需要根据具体的问题进行适当的调整和扩展。

x = model.addMVar(name="x", lb=0.0, ub=GRB.INFINITY, shape=10)

这行代码使用 Gurobi Python API 创建了一个名为 x 的变量。

在这行代码中，我们使用了 addMVar 方法，它用于向模型中添加变量。

• 参数 name 指定了变量的名称，
• lb 和 ub 分别指定了变量的下界和上界，
• shape 指定了变量的维度（这里是 10 维）。
• GRB.INFINITY 表示正无穷。

因此，这行代码创建了一个包含 10 个元素的实数变量数组 x，每个元素的取值范围是大于等于 0 的实数。

KKT 方法（Karush-Kuhn-Tucker 方法）是用于求解约束优化问题的一种数学方法。它基于 KKT 条件，这是一组必要条件，用于判断在最优解处，对于有约束的优化问题，某个点是否为最优解。

KKT 方法适用于以下形式的优化问题：

最小化 f(x)（或最大化 -f(x)）
满足 g(x) <= 0 和 h(x) = 0 的约束条件
其中，f(x) 是优化目标函数，g(x) 是不等式约束，h(x) 是等式约束。

KKT 方法通过以下一组条件来判断某个点 x 是否为最优解：

1. 约束条件的松弛条件：g(x) <= 0 和 h(x) = 0
2. 目标函数的梯度为零：∇f(x) + ∑(λ_i * ∇g_i(x)) + ∑(ν_i * ∇h_i(x)) = 0
3. λ_i >= 0（对于不等式约束）和 λ_i * g_i(x) = 0
4. ν_i（对于等式约束）没有限制

其中，λ_i 和 ν_i 分别是 Lagrange 乘子，用于将约束条件考虑到目标函数中。

KKT 方法的基本思想是通过引入 Lagrange 乘子，将约束条件考虑到目标函数中，然后通过求解 KKT 条件来判断某个点是否为最优解。如果满足 KKT 条件，则该点可能是最优解之一。

KKT 方法在数学优化领域中被广泛应用，特别是在非线性规划和凸优化问题中。它为判断最优解提供了一种有效的方法，并且为许多优化算法的理论基础。

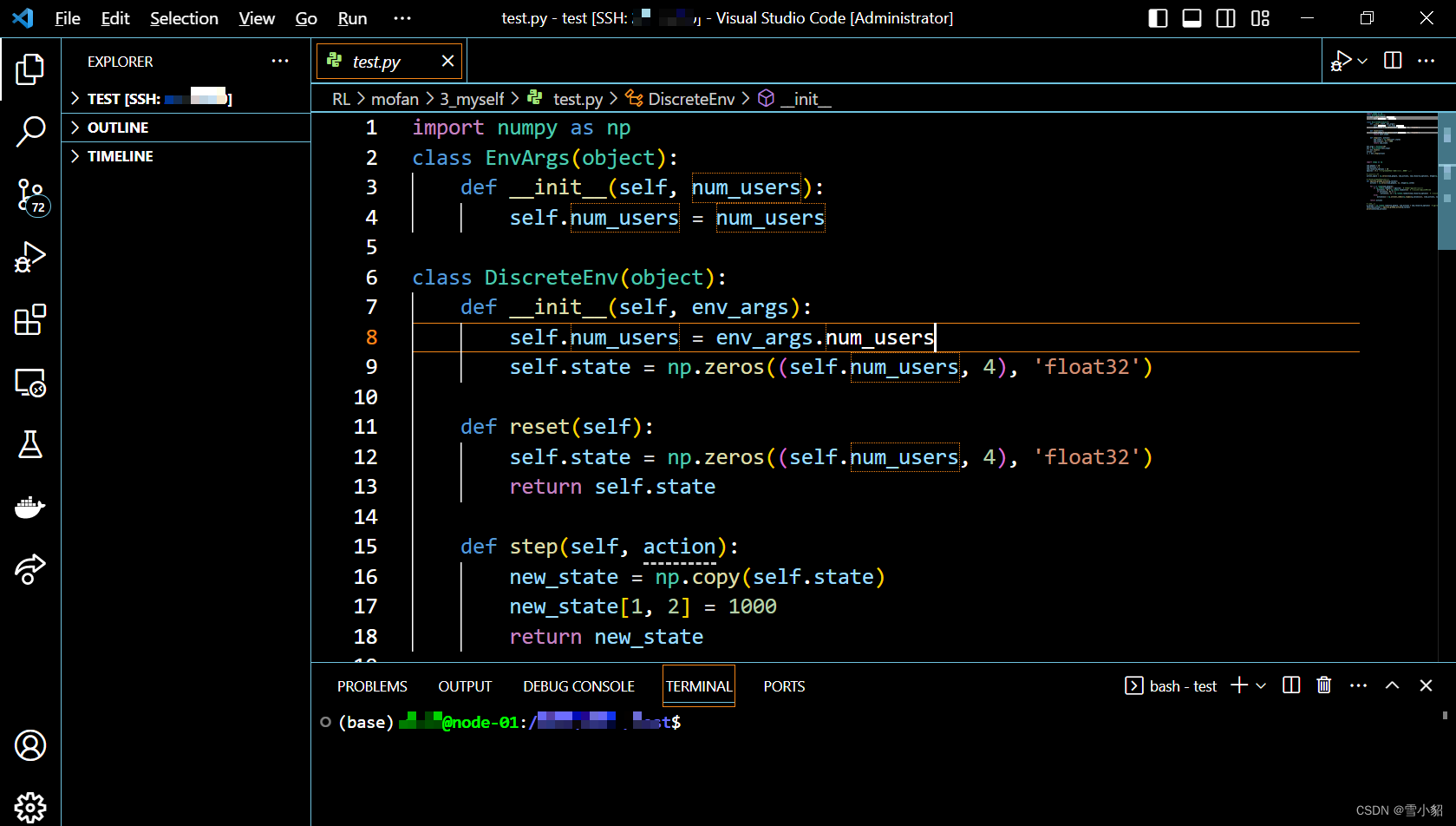
这行代码是针对一个优化问题中的目标函数值和下界进行更新的操作。让我来解释一下：

MP_obj = MP.ObjVal  # 获取当前优化问题的目标函数值
LB = max(MP_obj, LB)  # 更新下界 LB，取当前目标函数值和原下界中较大的那个

• 这段代码中，MP.ObjVal 是获取当前优化问题的目标函数值。这表示求解器（例如 Gurobi）已经找到了一个解，并计算出了对应的目标函数值。
• 然后，LB = max(MP_obj, LB) 这行代码用来更新下界 LB。它比较当前的目标函数值 MP_obj 和之前的下界 LB，然后取其中较大的那个作为新的下界。
• 在优化算法中，维护一个下界是很常见的。这是因为在一些优化算法中，我们可能无法找到全局最优解，但是我们可以找到一个较好的局部最优解。通过不断更新下界，我们可以逐渐缩小最优解的搜索范围，从而更接近全局最优解。

SP.addConstr(pi1 <= bigM*v, name='v1')
G3 = SP.addConstr(G@y-h+E@x.x+M@u <= bigM*(1-v), name='v2')
SP.addConstr(pi2 <= bigM*l, name='l1')
G4 = SP.addConstr(G1@y-h1+E1@x.x+M1@u <= bigM*(1-l), name='l2')
SP.addConstr(y <= bigM*w, name='w1')

解决了python中的图表显示问题，我好厉害，哈哈哈 

def plot_figure():plt.figure(1)Pg = plt.bar(range(24),y.x[:24])plt.figure(2)Ps_ch = plt.bar(range(24),y.x[24:48])plt.figure(3)Ps_dis = plt.bar(range(24),y.x[48:72])plt.figure(4)Pdr = plt.bar(range(24),y.x[72:96])plt.figure(5)Pbuy = plt.plot(range(24),y.x[144:168])Psell = plt.plot(range(24),y.x[168:192])plt.figure(6)Ppv = plt.plot(range(24),y.x[192:216])Pl = plt.plot(range(24),y.x[216:240])
plot_figure()

这段代码定义了一个名为 plot_figure 的函数，该函数用于绘制图表。具体来说，该函数使用了一个名为 plt 的库来进行图表绘制，其中 plt 可能是指 matplotlib 库。函数中的代码按顺序创建了六个不同的图表，并在每个图表中绘制了不同的条形图或折线图。

• - 在第一个图表中，使用 plt.bar 绘制了一个条形图 Pg，其中 x 轴的取值范围为 0 到 23，对应 y.x 中的前 24 个元素。
• - 在第二个图表中，绘制了另一个条形图 Ps_ch，同样的 x 轴取值范围，对应 y.x 中的第 25 到 48 个元素。
• - 接着在第三个图表中，绘制了 Ps_dis 条形图，对应 y.x 中的第 49 到 72 个元素。
• - 在第四个图表中，绘制了 Pdr 条形图，对应 y.x 中的第 73 到 96 个元素。
• - 然后在第五个图表中，绘制了 Pbuy 和 Psell 两个折线图，分别对应 y.x 中的不同范围的元素。
• - 最后在第六个图表中，绘制了 Ppv 和 Pl 两个折线图，同样对应 y.x 中的不同范围的元素。

总的来说，这段代码的功能是将一些数据以条形图或折线图的形式进行可视化展示。

以下是一个简单的基于 Python 的代码示例，用于使用 matplotlib 库创建并显示一个简单的折线图：

import matplotlib.pyplot as plt# 创建数据
x = [1, 2, 3, 4, 5]
y = [2, 3, 5, 7, 11]# 绘制折线图
plt.plot(x, y)# 添加标题和标签
plt.title('Simple Line Plot')
plt.xlabel('X')
plt.ylabel('Y')# 显示图表
plt.show()

• 在这个示例中，我们首先导入了 matplotlib.pyplot 库，然后创建了一些简单的数据。接下来，使用 plt.plot() 函数绘制了一个折线图，并使用 plt.title()、plt.xlabel() 和 plt.ylabel() 函数添加了标题和标签。最后，使用 plt.show() 函数显示了图表。
• 当你运行这段代码时，会弹出一个新的窗口来显示折线图。你可以在这个窗口中查看图表的绘制结果，并进行交互操作。

但是目前还是不懂他的编程，为啥这样编啊，啊啊啊 

intelligent control

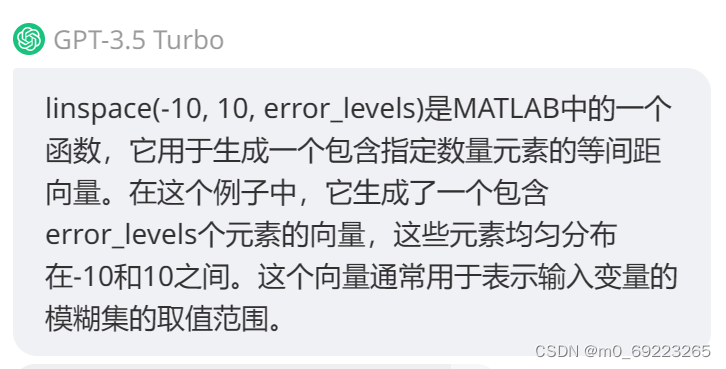
linspace(-10, 10, error_levels)

a=addvar(a,'input','e',[-3,3]);            %Parameter e
a=addmf(a,'input',1,'NB','zmf',[-3,-1]);
a=addmf(a,'input',1,'NS','trimf',[-3,-1,1]);
a=addmf(a,'input',1,'Z','trimf',[-2,0,2]);
a=addmf(a,'input',1,'PS','trimf',[-1,1,3]);
a=addmf(a,'input',1,'PB','smf',[1,3]);

a=addmf(a,'input',1,'PS','trimf',[-1,1,3]);

 

rulelist=[1 1 1 1;         %Edit rule base2 2 1 1;3 3 1 1;4 4 1 1;5 5 1 1];a=addrule(a,rulelist);